活性化関数(Activation function)とは?:AI・機械学習の用語辞典
用語「活性化関数」について説明。人工ニューラルネットワークにおける、ある1つのニューロンにおいて、入力を受けて、次のニューロンへ出力するために行う「非線形変換の処理(関数)」もしくは「恒等関数」を指す。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
用語解説
AI/機械学習のニューラルネットワークにおける活性化関数(Activation function)とは、あるニューロンから次のニューロンへの出力過程において、入力された数値を特定の方法で変換し、その結果を出力する関数のことである。
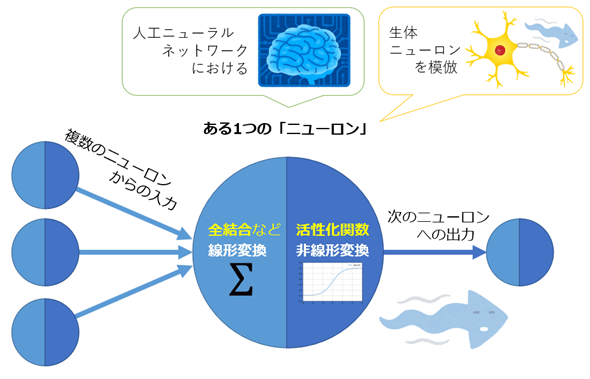
機械学習における人工ニューラルネットワーク(ANN:Artificial Neural Network)は、人間における生体ニューラルネットワーク(BNN:Biological Neural Network)の基本的な挙動を模倣している。人間のBNNでは、生体ニューロンが活性化(activation)することによって、電気信号がそのニューロンから次のニューロンへと伝播(でんぱ、※「伝搬:でんぱん」ではないので注意)していくことになる。ANNで、この「活性化」を表現するのが、活性化関数である。
複数のニューロンから、あるニューロンへの入力は、全結合(Fully connected)などの線形変換(Linear transformation、線形写像)処理によって1つの数値にまとめられる。活性化関数は、その数値を次のニューロンに「どのように出力するか」、つまり「どう活性化するか」が定義されたものだ(※よって活性化関数で重要なのは、「数式自体」よりも「どのような形状のグラフになっているか」である。形状については、例えばシグモイド関数のグラフ図を参照)。
この活性化の変換は、非線形変換(Non-Linear transformation、非線形写像)である必要がある(※線形変換を何度重ねても線形にしか変化せず、意味がないので)。図1は、「複数のニューロンからの入力」→「線形変換」→「非線形変換」→「次のニューロンへの出力」の流れを示した図である。※ただし出力層では、次のニューロンへの伝播がないため、活性化関数として「恒等関数」と呼ばれる線形変換が用いられることもある。
使われる活性化関数は時代とともに変化している。ニューラルネットワークの基礎となっている情報処理モデル「パーセプトロン」では「ステップ関数」という活性化関数が用いられていた。しかし、「バックプロパゲーション」が登場してからは「シグモイド関数」や「tanh関数」が使われるようになった。さらに、最近のディープニューラルネットワークでは「ReLU」がよく使われるようになっている。
また、出力層においてよく使われる主な活性化関数としては、
- 分類問題(二値)の場合は「シグモイド関数」
- 分類問題(多クラス)の場合は「ソフトマックス(Softmax)関数」
- 回帰問題の場合は「(活性化関数なし)」もしくは(前述した)「恒等関数」
がある。出力層の活性化関数の種類に応じて、使われる「損失関数」にもある程度のパターンがある。その具体的なパターンは表1にまとめた(※「交差エントロピー」など一部の損失関数については後日解説予定)。
| \ | 分類問題(二値) | 分類問題(多クラス) | 回帰問題 |
|---|---|---|---|
| 出力層の活性化関数 | シグモイド関数 | ソフトマックス関数 | (なし)/恒等関数 |
| 対応する損失関数 | 二値用の交差エントロピー(Binary cross entropy)誤差 | 多クラス用の交差エントロピー(Categorical cross entropy)誤差 | 平均二乗誤差(MSE) |
| 表1 出力層に使われる主要な活性化関数と、それに対応する損失関数のパターン | |||
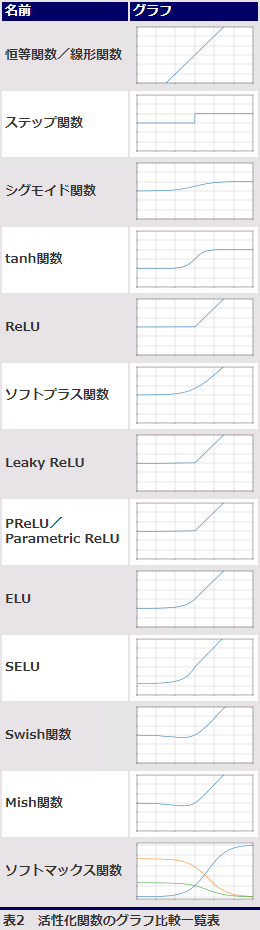
活性化関数のグラフ比較
表2は、本用語辞典で掲載している活性化関数の比較表である。各解説ページへのリンクも箇条書きで掲載した。
ここを更新しました(2024年1月15日)
定義の説明をより分かりやすく書き直しました。「後日解説」となっていて、解説されていない部分を修正しました。
Copyright© Digital Advantage Corp. All Rights Reserved.