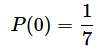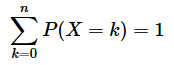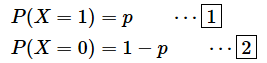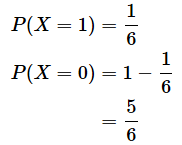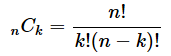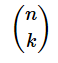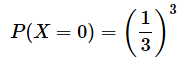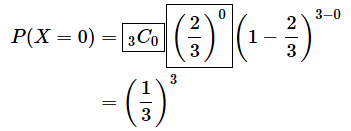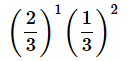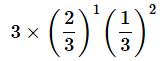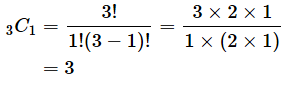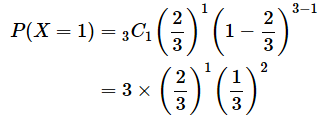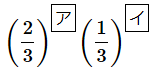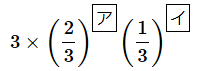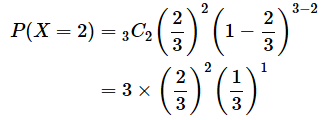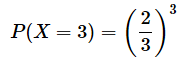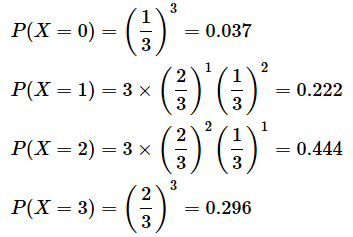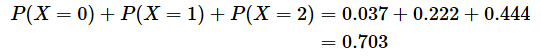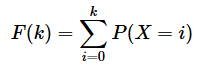[AI・機械学習の数学]確率分布の基本、ベルヌーイ分布、二項分布を理解する:AI・機械学習の数学入門
分類や推定・予測など、機械学習のさまざまな手法の基礎をなす「確率と統計」における「確率分布」とはどのようなものか。離散分布や連続分布といった種類に分けられるが、その一つである離散分布の例としてベルヌーイ分布と二項分布について見ていく。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
前回までは、特定の事象(できごと)が起こる確率の取り扱いやベイズの定理などについて見てきました。ここからは「確率分布」について見ていきます。
確率分布とは、全ての事象に対する確率を洗い出して、それらの事象がどのような確率で起こるかを表したもの……いわば全体像を表したものと考えていいでしょう。といっても、抽象的すぎて何のことか分からないかもしれませんね。しかし、具体例を見れば「なんだそんなことか」と簡単に分かる話です。
ここでは「分布」とはそもそもどういうものか、ということから始め、今回は離散分布の例としてベルヌーイ分布と二項分布を、次回は連続分布の例として正規分布とベータ分布を紹介します。併せて次回、ごく簡単にではありますが、事前分布や事後分布など、ベイズ統計に関する話題についても触れます。具体的には、今回と次回で以下のようなトピックを扱います。
目標と解説【その1】: 分布と確率分布
まずは「分布」がどういうものであるかを確認しておきましょう。分布とは、それぞれの事象がどれだけの頻度で起こるかということを表したものと考えられます。例えば、スポーツくじ「TOTO BIG」や「TOTO MEGA BIG」の第1216回の対象となったサッカーの試合では、各試合の得点の合計は以下のようになっていました。
2, 4, 5, 2, 4, 5, 4, 1, 0, 4, 0, 1, 3, 2
最初の2というのは、レヴァー対ブレーメンの結果が1対1だったので、合計が2点ということです。次の4というのは、ウニオン対ヴォルフスの結果が2対2だったので、合計が4点ということですね。それ以降の数字も同様にして求めた合計点です。これらの得点を分かりやすくまとめると以下のような表になります。
| 点数 | 度数 |
|---|---|
| 0 | 2 |
| 1 | 2 |
| 2 | 3 |
| 3 | 1 |
| 4 | 4 |
| 5 | 2 |
| 合計 | 14 |
| 表1 サッカーの合計得点の度数分布表 | |
このような表を度数分布表と呼びます。「度数」というのは「頻度」と同じ意味です。つまり、それが何回あったか、ということです。度数分布表を見ると、合計得点が0点だった試合が2回、1点だった試合が2回、2点だった試合が3回……といったぐあいに整理されていることが分かりますね。度数分布表をグラフ化しておくと、全体像も見やすくなります(図1)。
このようにして度数分布表をグラフ化したものをヒストグラムと呼びます。分布が一目で分かりますね。
続いて「確率分布」について見てみましょう。確率分布とは、度数(ヒストグラムの縦軸)を確率で表したものです。上の例では、表2のようになります。全体の度数つまり試合数が14なので、それぞれの度数を14で割れば求められますね。
| 点数 | 確率 |
|---|---|
| 0 | 1/7 |
| 1 | 1/7 |
| 2 | 3/14 |
| 3 | 1/14 |
| 4 | 2/7 |
| 5 | 1/7 |
| 合計 | 1 |
| 表2 サッカーの得点合計の確率分布 | |
ヒストグラムの方は縦軸の値が変わるだけで、形は全く同じなので省略します。この場合の点数を変数Xで表すと、例えば、X=0の確率は1/7となります。このような変数Xのことを特に確率変数と呼びます。……という話をいちいち日本語で書くのは冗長なので、数式にして簡潔に表現してみましょう(図2)。
となります。この式の「X=」を省略して、以下のように簡単に表すこともあります。
ここで大事なことは、確率分布では、全体の合計が1になるということです。これも数式で表せます。合計を表すにはΣが使えましたね。
ここまでは、分布と確率分布を理解するために、実際のデータを使った統計的確率の例を見てきました。次に、理論(モデル)に従って確率を計算した例、つまり数学的確率の例についても見ていきましょう。そのような場合には、確率が数式で表せるので、分布も数式だけで表すことができます。もちろん、度数分布表やヒストグラムを作ると直感的に全体像が把握できるので分かりやすくなりますが、確率分布が1つの数式だけで表せるというのが重要なポイントです。
目標【その2】: ベルヌーイ分布とは
結果が2つの場合に分かれるような試行をベルヌーイ試行と呼びます。例えば、コインを投げると表か裏が出ます(立つこともまれにありますがそれについては考えないことにします)。表が出ることを1、裏が出ることを0と表し、表が出る確率をpとすると、
と表されます。これは、以下のような1つの式で表すこともできます。
k=1のときは、後ろの(1−p)1−kが1になり、[1]式と一致します。また、k=0のときは、前のpkが1になり、[2]式と一致します。
このような分布をベルヌーイ分布と呼びます。後でグラフを示しますが、2つのうちの1つに決まる最もシンプルな分布です。
解説【その2】: ベルヌーイ分布とは
これからさまざまな確率分布を見ていきますが、モデルを表すにはできるだけシンプルなものから始めるのが鉄則です。というわけで、最もシンプルなベルヌーイ分布から見ていきます。最初に、公式の意味を確認しておきましょう(図3)。まだ実感が湧かないかもしれませんが、ぜひ、番号順に指さし確認しながら読んでみてください。
では、具体例です。【目標】のところでちらっと触れたコイン投げの例で見ていきましょう。コインを投げるとほぼ1/2の確率で表か裏が出ますが、それではつまらないので、表が0.6の確率で出るイカサマコインであるものとしましょう。表が出ることを目的の事象として、1と表せば、P(X=1)が0.6、P(X=0)が0.4であることは計算しなくても明らかです。ですが、数式での表現に慣れるために、あえて公式に当てはめてみましょう。
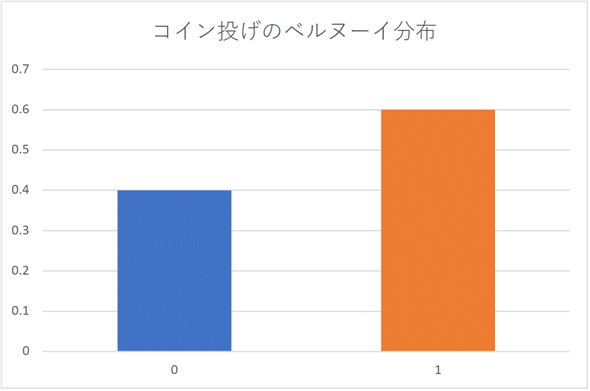
どのような値でも0乗すると1になることを覚えていれば簡単ですね。グラフも描いておきましょう(図4)。
グラフを見ても明らかなように、ベルヌーイ分布では、確率変数Xの値は0,1という飛び飛びの値になります。このように確率変数が飛び飛びの値になっている分布のことを離散分布と呼びます。離散分布には、次に見る二項分布のほかに、離散一様分布、ポワソン分布、超幾何分布などがあります。
ここでは、コイン投げの例を見ましたが、他にもさまざまな例があります。立方体のサイコロには6つの目がありますが、1の目が出る場合とそれ以外の目が出る場合に分ければ、ベルヌーイ分布となります。例えば、どの目も偏りなく出るものとして、1の目が出る場合を1、それ以外の目が出る場合を0とすれば、
となりますね。受け取ったメールが迷惑メールであるかそうでないか、明日の天気が晴れかそうでないかなど、ベルヌーイ分布で表せる事例は数多くあります。
目標【その3】: 二項分布とは
二項分布とは、複数のベルヌーイ試行を行ったときに、それぞれの事象が起こる確率の分布を表したもので、以下の式で表されます。
式が少し複雑になってきましたが、ベルヌーイ分布の公式と似ている部分があることに気がつきますね。二項分布はベルヌーイ試行を何回か行った場合の分布なので、何となく納得できると思います。後で具体例を見ていくので、ここでは大まかな意味をざっと確認しておきましょう。
まず、左辺の意味です。P(X=k)は、n回の試行でその事象がk回起こる確率を表します。例えば、コインを10回投げて、6回表が出る確率であれば、P(X=6)と表されます。この場合、n=10ですね。
次に右辺です。nCkはn個の中からk個選ぶ組み合わせの数です*1。これは、
で求められます。「C」は「Combination(組み合わせ)」の頭文字で、nCkは、「シー、エヌのケー」と読んだり、「コンビネーション、エヌのケー」と読んだりすることが多いようです。
n!はnの階乗を表します。つまり、
です。
pは目的の事象が起こる確率を表します。例えば、表と裏が偏りなく出るコインで、表が出ることを目的の事象とすると、p=1/2です。
例えば「1/2の確率で表か裏が出るコインを10回投げて6回表が出る」ということを公式に当てはめると、
となります。これを計算すると、答えは0.205となりますが、具体的な計算の方法については、以下の解説のところで見ていきましょう。
解説【その3】: 二項分布とは
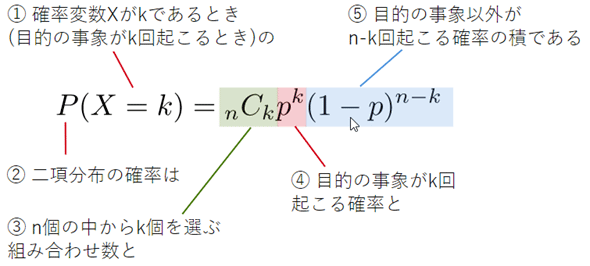
まず、以下の図で二項分布の公式を丁寧に確認しておきましょう。n回のベルヌーイ試行を行ったときに、目的の事象がk回起こる確率を求める式でしたね。ここでも、番号順に指さし確認しながら読んでみてください。
次に、なぜこのような式になるのか、具体例を使って見ていきましょう。動画の解説も用意してあるので、考え方をゆっくりと追いかけたい方はぜひ参照してください。動画では文章だけよりも動きが見えるのでより理解しやすいはずです。
動画1 二項分布
ここでは、話を簡単にするために、コイン投げの例を使いましょう。コインを3回投げたときに、表が何回か出る確率を求めてみます。まず、公式を使わずに、どのような結果になるかを地道に列挙していきましょう(表3)。表における()内の数字は単に事象を区別するためにつけた番号です。
表が出る確率をpとすると、裏が出る確率は1−pです。表も裏も同じように出るコインであれば、p=1/2なので、1−pも1/2となります。その値を使ってもいいのですが、やはり同じ確率だとつまらないので、ここでは、表がp=2/3の確率で出るイカサマコインであるとしましょう。すると、裏が出る確率は1−p=1/3ですね。
まず、表が0回出る確率P(X=0)について見ていきます。これは(1)に当たります。3回の試行は独立なので、
1 1 1
・(1)の裏裏裏が出る確率は ── × ── × ──
3 3 3
です。このような場合は1通りだけなので、
となります。これは簡単でしたね。
では、二項分布の公式にも当てはめてみましょう。n=3、k=0、p=2/3の場合に当たるので、以下のようにして求められます。枠で囲んだ部分は1になります。
実際に数えてみた結果と、公式を使って計算した答えとがちゃんと一致していますね。では、次に表が1回出る確率、つまり(2)〜(4)について見てみましょう。
2 1 1
・(2)の表裏裏が出る確率は ── × ── × ──
3 3 3
1 2 1
・(3)の裏表裏が出る確率は ── × ── × ──
3 3 3
1 1 2
・(4)の裏裏表が出る確率は ── × ── × ──
3 3 3
です。これらはいずれも、
と表せます。これが3通りあるわけなので、表が1回だけ出る確率は、
ですね。3通りというのは3つの中から1つを選ぶ組み合わせの数、つまり3C1になっていることに注目です*2。ここでは、これ以上の計算はしないことにします(公式を使った場合と一致するかどうかを見たいだけなので)。
では、公式に当てはめてみましょう。
はい、当然のことですが、答えは一致しています。
ここまでで、だいたい要領は分かってきたと思います。表が2回出る確率、つまり(5)〜(7)については、穴埋めで見ていきましょう。オレンジ色の部分をクリックまたはタップすれば答えが表示されます。
2 2 1
・(5)の表表裏が出る確率は ── × ── × ──
3 3 3
2 1 2
・(6)の表裏表が出る確率は ── × ── × ──
3 3 3
1 2 2
・(7)の裏表表が出る確率は ── × ── × ──
3 3 3
です。これらは表が2回、裏が1回なので、確率はいずれも、
(答え: [ア]= 2 、[イ]= 1 )
となります。これも3通りあるので、表が2回だけ出る確率は、
(答え: [ア]= 2 、[イ]= 1 )
です。この3通りというのは3つの中から表を2つ選ぶ組み合わせの数、つまり3C2の値です。
では、これについても、公式に当てはめた場合を見てみましょう。
やはり、答えは一致しています。最後の表が3回出る確率、つまり(8)については結果を記しておくだけで十分でしょう。
というわけで、具体的な例で全ての場合を列挙してみれば、二項分布の公式の意味もよく分かりますね。それぞれの値を実際に計算してみましょう*3。
*3 合計が1になっていないのは、小数点以下第4位を四捨五入しているためです。
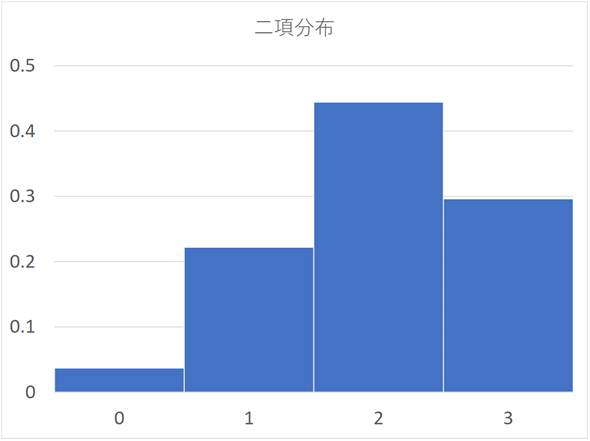
以上の計算結果をヒストグラムにしてみると図6のようになります。
母数、確率質量関数、累積分布関数などについて
二項分布は、さまざまなkに対して答えが求められます。従って、kに対する関数と考えられます。そこで、関数の書き方を使って、
などのように表すこともできます。このとき、nとpは関数の特徴を決める値となっています。そのような値のことを母数やパラメータと呼びます。母数が与えられると関数の特徴が決まるわけですが、これは、一次関数f(x)=ax+bになぞらえて考えると分かりやすいです。f(x)がxに対する関数であり、aやbが関数の特徴を決める値になっているのと同じようなものです。
ところで「母数が与えられたとき」というのは条件付き確率の表現と同じですね。というわけで、母数を明示するために「条件付き」を表す|を使って、
のように書くこともあります。なお、このような離散分布の確率変数に対応する値を表す関数(二項分布の公式で表されるような関数)のことを確率質量関数と呼びます。
二項分布のグラフを見ると、「表が2回まで出る確率」も求められることが分かりますね。これは「表が0回出る確率」+「表が1回出る確率」+「表が2回出る確率」なので、
となります。この式では、kの値を0から2まで変えながら順に足しているので、Σを使って表せることも分かります。つまり、目的の事象がk回まで出る確率をF(k)とすると、
となります。このF(k)は、kまでの確率を累積した(全部足した)確率になっているので、累積分布関数と呼ばれます。
コラム 尤度(ゆうど)について
二項分布の母数はnとpですが、nとkが決まっている場合は、pがさまざまな値を取る場合の分布が求められます。例えば、3回のうち2回表が出る場合を考えると、
となります。ベイズ統計では、f(k|p)が尤度となります。この例であれば、確率がpであるときにk=2、つまり2回表が出る「もっともらしさ」を表しているわけです。なお、kの値は確率変数の値、つまり結果(データ)を表すので、ベイズ流にDと書き、母数(パラメータ)をθと書けば、尤度は一般的に(二項分布に限らず)、
と表されます。
次回は……
今回は、確率と統計における確率分布のうち、離散分布の例としてベルヌーイ分布と二項分布などについて見てきました。続編である次回は、連続分布の例として正規分布とベータ分布を紹介し、ごく簡単にではありますが、事前分布や事後分布などベイズ統計に関する話題についても触れます。
Copyright© Digital Advantage Corp. All Rights Reserved.

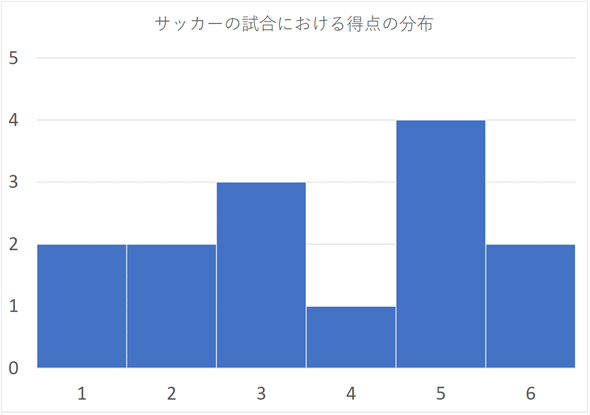
 図2 確率変数と分布の確率を数式で表す
図2 確率変数と分布の確率を数式で表す