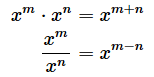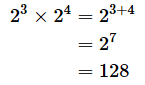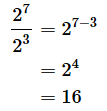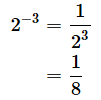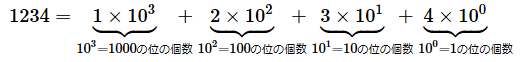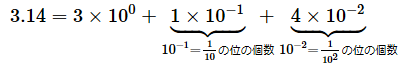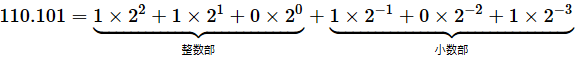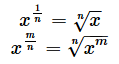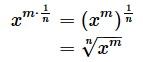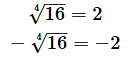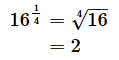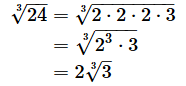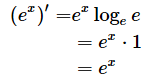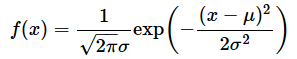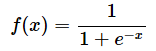[AI・機械学習の数学]指数と対数(指数編):AI・機械学習の数学入門
連載の通常の流れとは別の番外編。AIや機械学習でよく使う「指数」を解説。指数関数の性質や指数関数の微分法についても簡単に紹介する。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
この連載の本編では、微分やベクトル、行列などのいわば数学の「縦糸」に当たるテーマを取り上げていますが、番外編では、さまざまなテーマにまたがる、いわば「横糸」に当たるテーマを取り上げます。今回は、AIや機械学習に登場する数式の中でよく使われる「指数」に焦点を当てることにします。なお、指数と切っても切り離せない「対数」については、番外編3で取り扱うことにします。
指数は、同じ数を何回か掛けることを簡単に表すのに使います。その「何回か」は自然数(1以上の整数)でなくても構いません。ここでは、有理数(負の数を含めて、分数で表せる範囲の値)について、指数の取り扱いを見ていきます。また、指数関数の性質や指数関数の微分法についても簡単に紹介します。
ポイント1 指数関数の基本公式
指数の計算方法については、本編の第1回や番外編1でも取り扱ったので、具体的な計算の例はそちらに譲ることとして、まずは基本公式をまとめておきましょう。ただ、公式だけだと実感が湧かないでしょうから、簡単な例も併せて示すこととします。
掛け算と割り算の公式
これらの式で、xに当たる値のことを「底(てい)」と呼びます。mやnは「指数」ですね。以下の例では、いずれも底は2です。
(例1)
(例2)
指数の部分が掛け算になっている場合は、以下のようになります。
指数の部分がさらに指数になっている場合は、以下のように右から左へと計算します。
番外編1でも説明しましたが、Excelでべき乗を表す演算子「^」を使って「=2^3^2」と入力すると、[A]のような計算方法になり、結果は、
となります。一方、Pythonでべき乗を表す演算子「**」を使って「=2**3**2」と入力すると[B]のような計算方法になり、結果は、
となります。
何を0乗しても1になる
これは、割り算の公式でm=nである場合に当たります。なお、00は定義されません(このような計算は許されません)が、0nは0です。
マイナス乗の場合
これは、割り算の公式でm=0である場合に当たります。
(例3)
コラム n進数のしくみと指数
私たちが普段使っている十進数は、各桁の値と10を底とした指数の積を全て足した値と考えられます。例えば、
となります。右端が1の位(100の位)です。この例だと、1の位が4個あるということですね。10の位(101の位)が3個、100の位(102の位)が2個、1000の位(103の位)が1個あるというわけです。指数に注目すると、左の桁に行けば指数が1増えることが分かります。逆に言うと、右の桁に行けば指数が1減るわけですね。そして、1の位の指数は0となります。
ここで、小数点以下を考えてみましょう。右に行けば指数が1減るので、1の位の右、つまり小数第一位の指数は−1になり、さらにその右の小数第二位の指数は−2になると考えられます。例えば、
と表せます。10−1=1/10=0.1となり、10−2=1/100=0.01となるので、3.14は、1の位(100の位)が3個、0.1の位(10−1の位)が1個、0.01の位(10−2の位)が4個集まった数であることが分かります。ちゃんと計算が合っていますね。
なお、Pythonのround関数やExcelのROUND関数で四捨五入の桁位置を指定する場合には、上記のように表現したときの「-指数」の値を指定します。例えば、Pythonで小数点以下第2位まで求めるときには10の-2乗の位まで求めるので、-(-2)つまり、2を桁位置として指定し、round(1.234,2)と書きます。結果は1.23ですね。round(4649,-1)なら10の1乗の位まで求めるので、結果は4650となります。
上のような表し方は何進数でも同じです。例えば二進数であれば、底が2になるだけのことです。例えば、110.101という二進数であれば、
と表せます。整数部は6ですね。小数部は2−1=1/21=0.5、2−3=1/23=0.125なので、0.625になります。つまり、二進数の110.101は十進数の6.625であることが分かります。
ポイント2 指数が分数の場合
指数が1/nである場合は、n乗根の主要根になります*1。まず、公式を記しておきます。
上の式の
とは、n乗するとxになるような値のことです。例えば、
は、3乗すると8になる値です。23=8なので、この値は2となります。なお、
と書きます。
下の式は、指数の部分がmと1/nの掛け算になっているものと考えられます。すでに見た[A]式、つまり、
で、nのところに1/nを書けば、
となりますね。
指数が分数の場合の例はこれまで出てこなかったので、少し見ておきましょう。
(例4)
(例5)
実際の計算はPythonなどのプログラミング言語やExcelなどにまかせてしまえばいいのですが、
なので、根号(√)の中を素因数分解し、素因数のn乗の形にして根号の外に出すと、式を簡単にできます。
(例6)
コラム Pythonで底が負の場合は√と1/2乗の結果が異なる
nの正の平方根は√nですが、これは、
と表すこともできます。ただし、nが負の場合は虚数(複素数)となります。Pythonでは、リスト1のようにべき乗で表した場合は複素数が返されます。
>>> (-4)**(12)
(1.2246467991473532e-16+2j)
-4の1/2乗は2j(jは虚数単位)となります。前の1.2246467991473532e-16は本来は0ですが、わずかな誤差が表示されています。
一方、リスト2のようにmathモジュールのsqrt関数を使って、引数に負の値を指定するとエラーになります。
>>> from math import sqrt
>>> sqrt(-4)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ValueError: math domain error
ポイント3 指数関数の値とグラフ
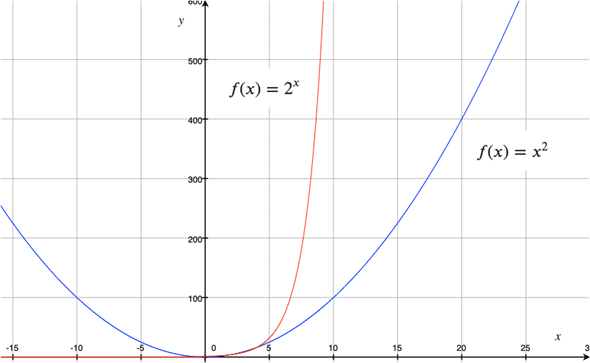
指数関数は、f(x)=axのように、変数xが指数になっているものです。f(x)=2xであれば、以下のような値になります。二次関数f(x)=x2との違いも見比べておきましょう。
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 二次関数 x2 | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 |
| 指数関数 2x | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
| 表1 二次関数と指数関数の値の変化 | |||||||||||
これだけの値を見ても分かるように、指数関数ではxの値が大きくなると急激にf(x)の値が大きくなります。グラフも描いておきましょう。
ポイント4 指数関数の微分法
指数関数の微分法については、公式と簡単な例を記すにとどめます。
のとき、
です。logは対数を表すので、対数の話をしないと上の式は使えませんね。というわけで、対数のお話をしましょう……といいたいところですが、それは番外編3で見ることとして、もう一つ重要な公式を記しておきます。
eは自然対数の底と呼ばれる値で、実際の値は2.7182... です。exを微分してもexになるというところが重要なポイントです。eは[C]式にもさりげなく登場していますね。
対数のお話をしないと指数関数の微分はできないのですが、雰囲気だけでもつかめるように、単に公式を適用しただけのものですが、簡単な具体例を記しておきます。
(例7)
(例8)
例8も公式を適用しただけですが、[D]が成り立つことが分かります。次回の番外編3で解説しますが、logee=1という公式も適用しました。
コラム 正規分布やシグモイド関数などで使われる自然対数の底e
自然対数の底eは、機械学習や統計学などのさまざまな場面で登場します。本編で紹介した正規分布の確率密度関数でも使われています。そこで見たように、exはexp(x)と表すことがあります。xの部分の式が複雑になるような場合に便利な表し方です。再掲しておきましょう。
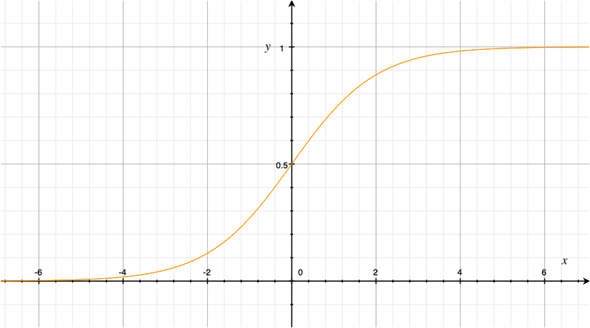
ほかにも、eはニューラルネットワークの活性化関数の一つであるシグモイド関数の中でも使われます。シグモイド関数は以下の式で表されます。
シグモイド関数をグラフ化すると以下のようになります。
活性化関数やシグモイド関数の詳細については、AI・機械学習の用語事典などをぜひ参照してください。
ここでは2つだけ例を挙げましたが、自然対数の底eは数学や物理などのさまざまな分野の数式に、頻繁に登場します。詳細については説明しませんが、世界一美しい数式として有名なオイラーの公式(eiπ+1=0)にも登場します。
今回は、指数の計算方法と指数関数、指数関数の微分法について簡単に整理しました。最後に、指数関数の微分に「対数」が必要であるということに少し触れましたが、対数については、次の番外編3で詳しく見ていくことにします。
Copyright© Digital Advantage Corp. All Rights Reserved.