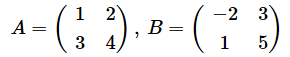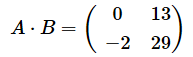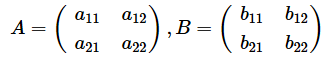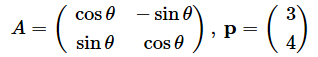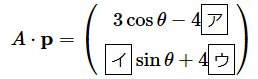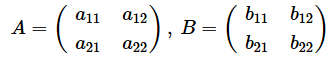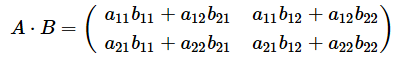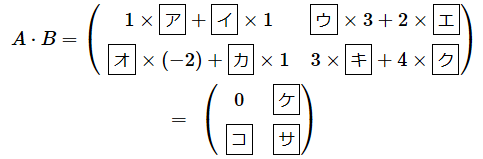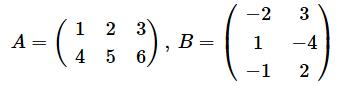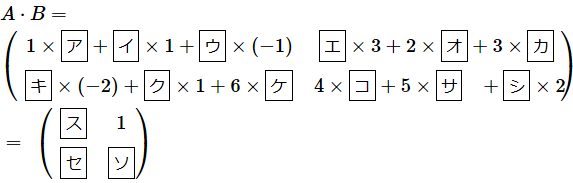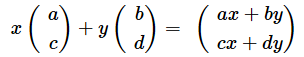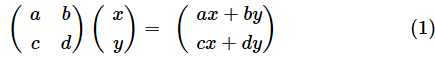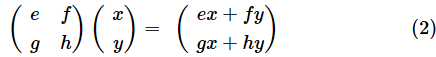Pythonで線形代数!〜行列編(基礎・後編):数学×Pythonプログラミング入門(1/4 ページ)
AI/機械学習で使われるデータを表現するためにはベクトルや行列などの線形代数を理解することが必要不可欠。今回は行列の内積の計算方法とその応用について、プログラミングの方法を初歩から見ていく。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
前回は、行列をNumPyの配列として表し、要素ごとの四則演算を行ったり、ブロードキャスト機能を利用したりする方法、さらに、行や列の操作、集計などについても見てきました。今回は行列の内積について基本的な考え方から計算方法、応用例について見ていきます。
この連載には「中学・高校数学で学ぶ」というサブタイトルが付いていますが、2012年施行の学習指導要領で数学Cが廃止され、行列が実質的に高校数学で取り扱われなくなったので、行列になじみのない方もおられるかもしれません。そこで、内積の計算方法についても簡単に説明することとします(なお、2022年度施行の学習指導要領では数学Cと行列が復活しました)。
行列の取り扱いについては内容が多岐にわたるので、少しずつ確実に理解できるよう、数回に分けて取り組むことにします。
- 基礎・前編(前回): 行列の表し方、四則演算、行や列の取り出し方、集計
- 基礎・後編(今回): 内積の考え方と、@演算子、inner関数、dot関数の働き
- 応用編: 行列式、固有値/固有ベクトルの利用
今回の練習問題としては、ニューラルネットワークに入力される値を計算するプログラムと、任意の点を中心にベクトルを回転させるプログラムを取り扱います。
連載:
『数学×Pythonプログラミング入門 ― 中学・高校数学で学ぶ』
この連載では、中学や高校で学んだ数学を題材にして、Pythonによるプログラミングを学びます。といっても、数学の教科書に載っている定理や公式だけに限らず、興味深い数式の例やAI/機械学習の基本となる例を取り上げながら、数学的な考え方を背景としてプログラミングを学ぶお話にしていこうと思います。
筆者紹介: IT系ライター、大学教員(非常勤)。書道、絵画を経て、ピアノとバイオリンを独学で始めるも学習曲線は常に平坦。趣味の献血は、最近脈拍が多く99回で一旦中断。さらにリターンライダーを目指し、大型二輪免許を取得するもバイクの購入資金が全くない。
目標1: 行列の内積を求める
前回の基礎・前編で少し紹介したように、内積は⋅という記号を使って、A ⋅ Bのように表すか、<,>を使って<A,B>と表します。ここでは⋅を使うことにします。
今回も、理屈は後回しにして、とにかくコードを書いて結果を求めることから取り組みましょう。簡単な例でやってみます。目標は、以下の行列のA ⋅ Bを求めるということです。
NumPyでは、内積は@演算子またはdot関数で求められます。厳密には@演算子とdot関数の働きは異なりますが、二次元の配列では同じ結果になります(三次元以上の配列では結果が異なります)。以下のような結果が得られれば正解です。
1. 行列の内積を求めるコードを書く
行列をNumPyの配列として表す方法は、前回の基礎・前編で学んだ通りです。内積を求めるために@演算子またはdot関数が使えることも分かっているので、コードを書くのはたやすいでしょう。リスト1の通りです。
import numpy as np
A = np.array([[1, 2],
[3, 4]])
B = np.array([[-2, 3],
[1, 5]])
print(A @ B)
print(np.dot(A, B))
# 出力例:
# [[ 0 13]
# [-2 29]] # @演算子で求めた内積
# [[ 0 13]
# [-2 29]] # dot関数で求めた内積
内積の計算結果は元の配列からは想像しづらいかもしれない。後述の解説で、計算方法を確かめておこう。np.dot(A, B)はA.dot(B)としてもよい。
はい、結果が求められました。しかし、どのような計算を行っているのかを理解していないと、適切に利用することができません。そこで、内積の計算方法を確認しておきましょう。
とすると、内積A ⋅ Bは、
で求められます。……とさらっと書きましたが、行と列を表す添え字が入り乱れていて、ちょっとややこしいですね。これを覚えないといけないかと思うと、ちょっと気がめいりそうです。しかし、理屈が分かれば丸暗記する必要はありません。
そこで、行列の内積を求める前に、行列とベクトルの内積の求め方を見ておきましょう。そうすると、行列同士の内積の計算方法も分かりやすくなります。また、上の式は2×2行列の場合にしか使えませんが、どんな場合にも使えるようになります。なお、以下のお話は、動画でも解説しているので、ぜひご視聴ください。
動画1 行列とベクトルの内積の求め方
では、行列とベクトルの内積です。
のとき、
となります。これは、Aの行とBの列の要素ごとの積和になっていることが分かります。筆者は「行列」の内積だから「行」と「列」を掛ければいい、と教わったような記憶がおぼろげながらありますが、そう覚えていた人も多いと思います(図1)。
行列とベクトルの内積では、行列がn行k列のとき、ベクトルはk行1列の形になっている必要があります*1。結果はn行1列になります。例えば、4行3列の行列と3行1列のベクトルの内積は、4行1列のベクトルになります。
*1 ただし、NumPyでは、n行k列の配列と、1行k列のベクトルの内積を求めることができます。その場合ベクトルはk行1列であるものと見なされて計算され、1行n列のベクトルが返されます。
まず、図1の計算を確実にするため、手計算での練習を挟んでおきましょう。といっても、単純な値の計算問題は退屈なので、ちょっとだけスパイスを加えたものにします。オレンジ色の部分をクリックまたはタップすると答えが表示されます。
のとき、
(答え)
[ア]= sinθ 、[イ]= 3 、[ウ]= cosθ
ちなみに、この計算の結果は、点p=(3, 4)を反時計回りにθラジアン回転させた点の座標となります。
行列とベクトルの内積の計算方法が分かれば、行列の内積の計算方法もその延長線上で理解できます。2×2行列の例で見てみましょう。
のとき、
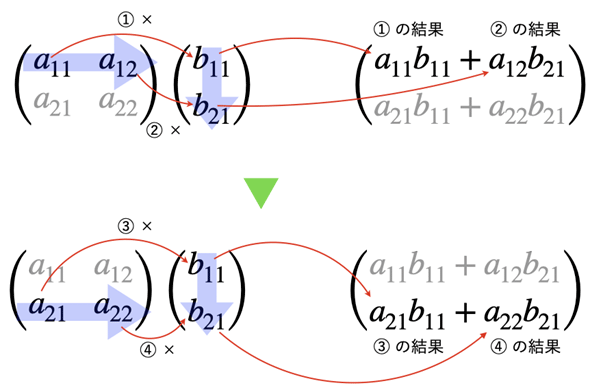
となります。これは、ベクトルをもう1つ横に並べ、図1と同じ方法で計算を行っただけです(図2)。
 図2 行列の内積の計算方法
図2 行列の内積の計算方法図の手順で考えれば行列とベクトルの内積の延長で理解できる。ただし、実際に手計算を行うときには、(1)(2)→(5)(6)→(3)(4)→(7)(8)の順に計算して、結果を左から右、上から下に求めていくことが多い。
計算方法を確実に理解するために、これについても手計算で練習しておきましよう。リスト1の答えを求めてみてください。オレンジ色の部分をクリックまたはタップすると答えが表示されます。
とすると、
(答え)
[ア]= (-2) 、[イ]= 2 | [ウ]= 1 、[エ]= 5 、
[オ]= 3 、[カ]= 4 | [キ]= 3 、[ク]= 5 、
| [ケ]= 13 、
[コ]= -2 | [サ]= 29
内積の計算では、行列の形に注意する必要があります。A ⋅ Bを求める場合、Aはn行k列、Bはk行m列になっている必要があります。結果はn行m列の行列となります。例えば、Aが2行3列で、Bが3行4列の場合、A ⋅ Bは2行4列となります。しかし、B ⋅ Aは計算できません。簡単な例で確かめておきましょう(リスト2、図3)。
import numpy as np
A = np.array([[1, 2, 3],
[4, 5, 6]]) # 2行3列
B = np.array([[-2, 3, 4, -3],
[1, 5, 1, 2],
[-3, -1, 2, 4]]) # 3行4列
print(A @ B)
print(B @ A)
# 図3が出力例
n行k列の配列とk行m列の配列の内積は求められるが、k行m列とn行k列の内積は求められない。
 図3 行列の内積を計算できない場合のエラー出力例
図3 行列の内積を計算できない場合のエラー出力例A@B(AとBの内積)は正常に求められる。
B@A(BとAの内積)を求めようとするとエラーになる。なお、エラーメッセージにmatmulという関数名が表示されているが、@演算子とmatmul関数とは同じ働き(Python3.5以降でmatmul関数と同じ働きを持つ演算子@が利用できるようになった)。
図2で見た考え方を理解していれば、どんな形の行列であっても、上で見た形に関するルールさえ満たしていれば計算の方法が分かるはずです。実際のところNumPyの@演算子やdot関数を使えば、計算方法を忘れてしまったとしても内積は求められますが、ちゃんと理解していることは大切です。練習問題で確認しておきましょう。オレンジ色の部分をクリックまたはタップすると答えが表示されます。
のとき、
(答え)
[ア]= (-2) 、[イ]= 2 、[ウ]= 3 | [エ]= 1 、[オ]= (-4) 、[カ]= 2
[キ]= 4 、[ク]= 5 、[ケ]= (-1) | [コ]= 3 、[サ]= (-4) 、[シ]= 6
[ス]= -3 | 、
[セ]= -9 | [ソ]= 4
コードを書いて、正しい結果が得られるかどうかも確認しておいてください(リスト3)。
import numpy as np
A = np.array([[1, 2, 3],
[4, 5, 6]]) # 2行3列
B = np.array([[-2, 3],
[1, -4],
[-1, 2]]) # 3行2列
print(A @ B)
# 出力例:
# [[-3 1]
# [-9 4]] # 結果は2行2列
2行3列の配列と3行2列の配列の内積なので、結果は2行2列となる。
コラム 基底ベクトルと一次変換で内積を理解する
内積の計算方法はルールを覚えてしまえば機械的にできます。上で見たように、行列とベクトルの内積から考えると覚えやすくなりましたが、それでも行と列が入り乱れてまだややこしいですね。しかし、なぜそんな計算をするのかさえ理解していれば、実は簡単にルールを導き出せます。また、応用にもつながります。少しそのお話をしましょう。
まず、ベクトルv=(x, y)をx方向の単位ベクトルex=(1, 0)とy方向の単位ベクトルey=(0, 1)に分けて表してみましょう。単位ベクトルとは長さが1のベクトルのことです。
このようにベクトルを一次式の和で表したときのexとeyを基底ベクトルと呼びます(基底ベクトルは単位ベクトルでなければならないということはありませんが)。
ここで、基底ベクトルexが(a, c)に、eyが(b, d)に移るように座標(空間そのもの)を変形したとします。このような変形を一次変換と呼びます。すると、ベクトルvも同様に動き、
に移ることになります。これは、以下のように基底ベクトルをそのまま並べて行列として表し、ベクトルに掛けた結果と一致します(図1とは使っている文字が異なりますが、同じ結果になっています)。
行列とベクトルの内積は、ベクトル(空間)を行列によって変形する操作に他ならないというわけです。行列の内積は、さらにもう一回変形を加えることを表します。例えば、
とし、
のように変形を行った後、
による変換を行うのであれば、(2)で求めた最初の変換後のベクトルに、さらに変換を行うための行列Aを左から掛ければいいですね。計算してみましょう。
計算結果をよく見ると、ベクトルv=(x, y)に対してBという変換を行った後、Aという変換を行うのと、ベクトルvに行列の内積A⋅ Bを左から掛けたものが等しいということが分かります。
基底ベクトルの考え方を理解していれば、線形代数が単なる計算としてではなく、図形的にも理解できるようになり、次回解説する行列式や固有値/固有ベクトルなどについての見通しがとても良くなります。なお、行列の内積では、結合法則A(BC)=(AB)Cは成り立ちますが、交換法則AB=BAは成り立ちません。
Copyright© Digital Advantage Corp. All Rights Reserved.


 羽山博
羽山博