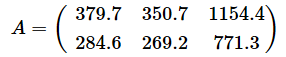Pythonで線形代数!〜行列編(基礎・前編):数学×Pythonプログラミング入門(1/5 ページ)
AI・機械学習で使われるデータを表現するためにはベクトルや行列などの線形代数を理解することが必要不可欠。今回は行列の各種計算や行、列の抽出、形状の変更方法などについて、プログラミングの方法を初歩から見ていく。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
前回は、ベクトルの基本的な計算方法と内積や外積の利用例についてのプログラミングに取り組みました。今回は行列の計算や変形を効率よく行うために利用できるNumPyの機能や関数を紹介します。
この連載には「中学・高校数学で学ぶ」というサブタイトルが付いていますが、2012年施行の学習指導要領で数学Cが廃止され、行列が実質的に高校数学で取り扱われなくなったので、行列になじみのない方もおられるかもしれません。そこで、基本的な考え方や四則演算などの計算方法についても簡単に説明することとします(なお、2022年度施行の学習指導要領では数学Cと行列が復活しました)。
行列の取り扱いについては内容が多岐にわたるので、少しずつ確実に理解できるよう、数回に分けて取り組むことにします。
- 基礎・前編(今回): 行列の表し方、四則演算、行や列の取り出し方、集計
- 基礎・後編: 内積の考え方と、@演算子、inner関数、dot関数の働き
- 応用編: 行列式、固有値/固有ベクトルの利用
今回の練習問題としては、画像を共通鍵方式によって暗号化/復号するプログラム、画像をRGBチャンネルに分解するプログラムの2つを取り扱います。画像に特化した話のように思われるかもしれませんが、可視化できる素材として取り上げただけです。画像以外のさまざまなデータの処理にももちろん応用できます。
連載:
『数学×Pythonプログラミング入門 ― 中学・高校数学で学ぶ』
この連載では、中学や高校で学んだ数学を題材にして、Pythonによるプログラミングを学びます。といっても、数学の教科書に載っている定理や公式だけに限らず、興味深い数式の例やAI/機械学習の基本となる例を取り上げながら、数学的な考え方を背景としてプログラミングを学ぶお話にしていこうと思います。
筆者紹介: IT系ライター、大学教員(非常勤)。書道、絵画を経て、ピアノとバイオリンを独学で始めるも学習曲線は常に平坦(たん)。趣味の献血は、最近脈拍が多く99回で一旦中断。さらにリターンライダーを目指し、大型二輪免許を取得するもバイクの購入資金が全くない。
目標1: 行列とは ― 行列とスカラーの四則演算を行う
行列とは、文字通り、数値や式を行と列に並べたものです。あまり難しく考えず、まずは、数値や式を行、列に並べると便利な計算ができるものだと考えていただくといいでしょう。簡単な例で見てみます。総務省統計局で公開されている賃金構造基本統計調査によると、10人以上の民営事業所における正社員/正職員の2020年の給与額(単位千円)は以下のようになっています。
| きまって支給する現金給与額 | 所定内給与額 | 年間賞与その他特別給与額 | |
|---|---|---|---|
| 男 | 379.7 | 350.7 | 1154.4 |
| 女 | 284.6 | 269.2 | 771.3 |
「きまって支給する現金給与額」などの意味については、行列の計算方法とは直接関係がないので、ここでは触れない。詳細は、厚生労働省の用語説明を参照されたい。
確かに表1のような形にまとめておくと意味は分かりやすいのですが、以下のように単純に並べ、Aなどの名前を付けておくと簡潔に表せます。
これが行列に他なりません。このように表せば「男性の所定内給与額」などと言わなくても、a12と書くだけで、1行2列目の値であることが分かります(行列の名前は大文字の斜体で、それぞれの成分は小文字で表すのが一般的です)。また、数式の中でも取り扱いやすくなります。
行列の形にも注目しましょう。この例では、行数が2行、列数が3列です。そのような場合には「2行3列の行列」あるいは「2×3行列」と呼びます。
行列に含まれる個々の値のことを数学では「成分」と呼びますが、ここでは「要素」と呼ぶことにします。また、数学では、行と列は1から数えるのが一般的なので、例えば、1行2列目の値は350.7で、2行3列目の値は771.3となります。しかし、PythonのリストやNumPyの配列を利用して行列を表す場合は、インデックスを0から数えるので、0行1列目が350.7、1行2列目が771.3となります。
ここで、簡単な計算を考えてみましょう。例えば、全ての金額を10%アップしたいとすれば、
あるいは
と表せます。掛け算の場合、数学では、定数(スカラー)は行列の前に書くのが一般的です。表のままだとこのように簡単に表せないですよね。ただし、全ての金額に10を足したいという場合には、数学では、
という表し方はしません*1。しかし、NumPyの配列ではそういう表し方もできます。
*1 数学では、行列にスカラーを足すことはできないので、例えば、Aの全ての要素に10を加える場合、Aと同じ形で、全ての要素が10である行列Bを考え、A+Bと表します。
そこで、行列をNumPyの配列として作成し、要素を取り出したり、計算を行ったりしてみましょう。以下のようなコードを書くのがここでの目標です。
- 上に示した行列AをNumPyの配列を使って表す
- 1行2列目の要素を取り出す(先頭を0と数えます)
さらに、以下のようなコードも書きましょう。
- Aの全ての要素に10を加えた配列を求める(全て1万円アップ)
- Aの全ての要素に1.1を掛けた配列を求める(全て10%アップ)
Pythonでは、1文字の変数名は推奨されていませんが、ここでは上の例と合わせるために、行列を表す変数名をAやBとします。また、これ以降「行列を表す配列」のことを単に「配列」と呼ぶことにします。
1. 配列を作成し、配列とスカラーの四則演算を行うコード
行列をPythonで取り扱うには、二次元のリスト(正確にはリストのリスト)やNumPyの二次元配列(ndarray)を使います。二次元のリストについては、本連載の第5回などで取り扱っていますし、行列の計算には断然NumPyが便利なので、今回はNumPyの配列を使うことにしましょう。
リスト1はその例です。numpyモジュールのarray関数に二次元のリストを指定すると、配列を作成できます。
import numpy as np
A = np.array([[379.7, 350.7, 1154.4],
[284.6, 269.2, 771.3]])
print(A)
print(A[1, 2])
# 出力例:
# [[ 379.7 350.7 1154.4]
# [ 284.6 269.2 771.3]]
# 771.3
作成した配列全体をprint関数を使って表示すると[]の中に各要素をスペースで区切って並べた形式で表示される。個々の要素を指定するには、インデックスを[行, 列]の形式で指定すればよい。
配列を作成するという目標が達成できたので、次に四則演算を行ってみます。
配列の全ての要素にスカラーを加えるには+演算子が使えます。また、全ての要素をスカラー倍するには*演算子を使います。リスト1の続きにリスト2のコードを入力して実行してみてください。
print(A + 10) # リスト1の続き
print(A * 1.1)
# 出力例:
# [[ 389.7 360.7 1164.4]
# [ 294.6 279.2 781.3]] # Aの全ての要素に10を加えた配列
# [[ 417.67 385.77 1269.84]
# [ 313.06 296.12 848.43]] # Aの全ての要素を1.1倍した配列
四則演算のための演算子を使って、配列とスカラーの和/差/積/商を求めると、配列の各要素に対してスカラーとの演算を行って得られた配列が求められる。//演算子、%演算子、**演算子なども同様。これらの演算子を使った配列同士の演算も要素ごとに行われる。
四則演算のための演算子を使って配列とスカラーの計算を行うと、配列の全ての要素に対してスカラーとの計算が行われます。既に何度も登場していますが、このように、1つの値と配列のそれぞれの要素との演算を行う機能をブロードキャスト機能と呼びます。ブロードキャスト機能のさらなる活用方法については、目標3で取り扱います。
なお、これまでに見たコードでは、配列Aの値が変わるのではなく、配列Aに対する演算を行って得られた配列が返されることに注意してください。配列Aの値そのものを変えたい場合はリスト3のようにします。
import numpy as np
A = np.array([[379.7, 350.7, 1154.4],
[284.6, 269.2, 771.3]])
A += 10
print(A)
# 出力例:
# [[ 389.7 360.7 1164.4]
# [ 294.6 279.2 781.3]] # Aの各要素の値が変わった
A += 10はA = A + 10と書いてもよい。要するに、計算して求められた配列を元の配列Aに代入すればよい。
Copyright© Digital Advantage Corp. All Rights Reserved.


 羽山博
羽山博