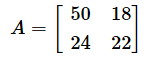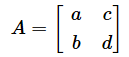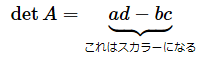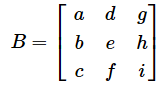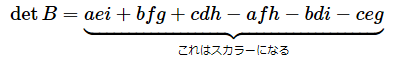Pythonで線形代数!〜行列・応用編(行列式・固有値):数学×Pythonプログラミング入門(1/5 ページ)
AI/機械学習で使われるデータを表現するためにはベクトルや行列などの線形代数を理解することが必要不可欠。今回は行列式と固有値/固有ベクトルの求め方、さらに、それらの応用について、プログラミングの方法を初歩から見ていく。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
前々回は、行列をNumPyの配列として表し、要素ごとの四則演算を行ったり、ブロードキャスト機能を利用したりする方法、さらに、行や列の操作、集計などについても見ました。前回は、行列の内積について基本的な考え方から計算方法を簡単に紹介するとともにNumPyの配列による基本的なプログラミングの方法、さらに応用例を見てきました。今回は線形代数の難所である行列式と固有値/固有ベクトルを求める方法と応用例を紹介します。
この連載には「中学・高校数学で学ぶ」というサブタイトルが付いていますが、2012年施行の学習指導要領で数学Cが廃止され、行列が実質的に高校数学で取り扱われなくなったので、行列になじみのない方もおられるかもしれません。そこで、行列式と固有値/固有ベクトルについて、必要最低限の考え方と計算方法も併せて紹介します(なお、2022年度施行の学習指導要領では数学Cと行列が復活しました)。
行列の取り扱いについては内容が多岐にわたるので、少しずつ確実に理解できるよう、数回に分けて取り組んでいます。
- 基礎・前編(前々回): 行列の表し方、四則演算、行や列の取り出し方、集計
- 基礎・後編(前回): 内積の考え方と、@演算子、inner関数、dot関数の働き
- 応用編(今回): 行列式、固有値/固有ベクトルの利用
今回の練習問題としては、行列式を利用してハート形の図形の面積を求めるプログラムと、分散・共分散行列の固有値/固有ベクトルを求めることにより主成分分析を行うプログラムを取り扱います。
連載:
『数学×Pythonプログラミング入門 ― 中学・高校数学で学ぶ』
この連載では、中学や高校で学んだ数学を題材にして、Pythonによるプログラミングを学びます。といっても、数学の教科書に載っている定理や公式だけに限らず、興味深い数式の例やAI/機械学習の基本となる例を取り上げながら、数学的な考え方を背景としてプログラミングを学ぶお話にしていこうと思います。
筆者紹介: IT系ライター、大学教員(非常勤)。書道、絵画を経て、ピアノとバイオリンを独学で始めるも学習曲線は常に平坦。趣味の献血は、最近脈拍が多く99回で一旦中断。さらにリターンライダーを目指し、大型二輪免許を取得するもバイクの購入資金が全くない。
目標1: 行列式の値を求め、基本的な性質を確認する
行列式は行と列の数が同じ正方行列の特徴を表す値の一つで、行列を応用するための基礎となる値です。行列Aの行列式は| A |またはdet Aと表します。
最初の目標は、以下の行列AをNumPyのndarrayとして作成し、行列式det Aの値を求めてみようというものです。
行列式の値は以下の公式を使って計算します。といっても、numpy.linalgモジュールまたはscipy.linalgモジュールのdet関数を使えば答えが求められるので、ムリに暗記する必要はありませんし、ここでも公式を使った計算をする必要はありません。ただ、式をざっと見て、行列式の値はスカラーであるということだけ確認しておいてください。スカラーとはベクトルや行列ではない、単なる数値のことです。
- 2×2行列の行列の場合
のとき、
- 3×3行列の場合
のとき、
となります。
また、以下の事柄についても確認しておきましょう。平行四辺形の面積や平行六面体の体積については、後で図解します*1。
- 行列Aの行列式は、行列Aの列ベクトル(a,b)と(c,d)で作られる平行四辺形の面積と等しい
- 行列Bの行列式は、行列Bの列ベクトル(a,b,c)、(d,e,f)、(g,h,i)で作られる平行六面体の体積と等しい
- 行列式の値が0の場合、逆行列は存在しない
- 行列式の値は負になることもある
といったところで、例題に取り組みましょう。668という答えが得られれば正解です。なお、numpy.linalgのlinalgは「線形代数」を意味するlinear algebraの略で、det関数は「行列式」を意味するdeterminantの略です。
*1 ここでは、必要最低限の考え方や取り扱い方法についてのみ説明するので、4×4以上の行列の行列式の計算方法など、詳細については別連載『AI・機械学習の数学入門 ― 中学・高校数学のキホンから学べる』の「番外編4 線形代数の行列式をマスター」を参照してください。
1. 行列式の値を求め、基本的な性質を確認するためのコードを書く
行列式の値を求めるだけなら簡単です。以下に示すリスト1の通りです。
import numpy as np
from scipy import linalg
A = np.array([[50, 18],
[24, 22]])
print("NumPyでの結果:", np.linalg.det(A))
print("SciPyでの結果:", linalg.det(A))
# 出力例:
# NumPyでの結果: 667.9999999999998
# SciPyでの結果: 668.0
公式に従って計算すると668になるが、numpy.linalgモジュールのdet関数ではわずかな誤差が出る。なお、import文をimport scipy as spとし、det関数の呼び出しをsp.linalg.det(A)とすると、module 'scipy' has no attribute 'linalg'というエラーが表示されることがある。今回は主にNumPyを使うことにする。
目標1で記した行列式の図形的な意味も確認しておきましょう(図1)。3×3の行列の行列式が平行六面体の体積になることについての図解は、上に記した記事を参照してください。
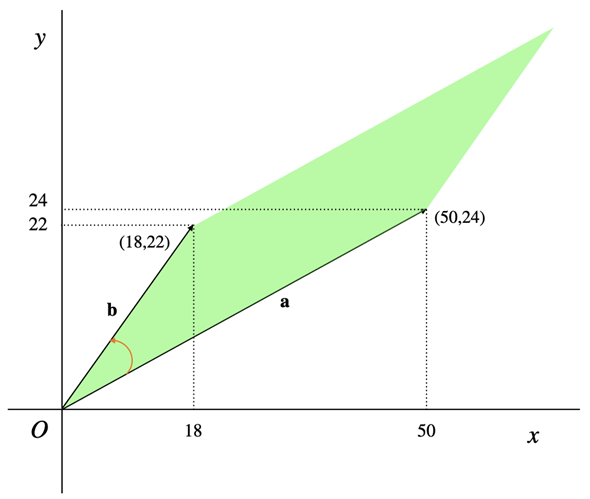 図1 2×2行列の行列式は列ベクトルで作られる平行四辺形の面積
図1 2×2行列の行列式は列ベクトルで作られる平行四辺形の面積例として示した行列の列ベクトルをa=(50,24),b=(18,22)とすると、行列式の値はこれらのベクトルを挟辺とする平行四辺形の面積となる。
行列式の値が0の場合というのは平行四辺形にならない場合です。いずれかのベクトルがどの成分(要素)も0である零(ゼロ)ベクトルの場合や、2つのベクトルが同一直線上にある場合などがそれに当たります。この場合、逆行列は存在しません。確認してみましょう。逆行列を求めるにはnp.linalgモジュールのinv関数を使います(invはinverseの略です)。
import numpy as np
A = np.array([[10, 20],
[20, 40]])
print("行列式の値:", np.linalg.det(A))
print("逆行列:", np.linalg.inv(A))
# 出力例
# 行列式の値: 0.0
# ---------------------------------------------------------------------------
# LinAlgError Traceback (most recent call last)
# <ipython-input-5-0d44b3ee5e9e> in <module>
# 4 [20, 40]])
# 5 print("行列式の値:", np.linalg.det(A))
# ----> 6 print("逆行列:", np.linalg.inv(A))
#
# <__array_function__ internals> in inv(*args, **kwargs)
#
# 1 frames
# /usr/local/lib/python3.7/dist-packages/numpy/linalg/linalg.py in _raise_linalgerror_singular(err, flag)
# 86
# 87 def _raise_linalgerror_singular(err, flag):
# ---> 88 raise LinAlgError("Singular matrix")
# 89
# 90 def _raise_linalgerror_nonposdef(err, flag):
#
# LinAlgError: Singular matrix
(10,20)と(20,40)は、いずれもy=2xという直線上にある。そのため、行列式の値が0になった(平行四辺形にならないので面積が0となった)。inv関数を使って逆行列を求めようとしてもエラーになる。
また、行列式の値は負になることもあります。面積を表すのに負の値はないでしょ、と思われるかもしれませんが、これがなかなかお役立ちな性質です(次の目標2で見ます)。例えば、最初に見たa=(50,24),b=(18,22)を入れ替えて並べた行列の行列式を求めてみると以下のようになります。
import numpy as np
A = np.array([[18, 50],
[22, 24]])
print("行列式の値:", np.linalg.det(A))
# 出力例:
# 行列式の値: -667.9999999999998
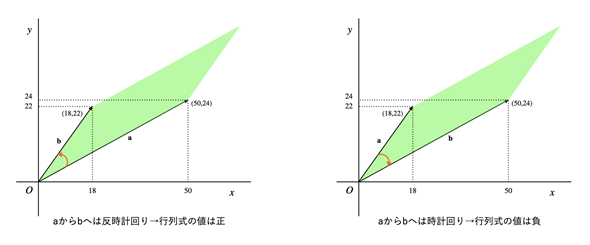
a=(18,22),b=(50,24)を行列にして、行列式の値を求めると負になる。
aから見てbが反時計回りの位置にある場合は行列式の値は正になり、時計回りの位置にある場合は行列式の値は負になります(図2)。時計回りか反時計回りかは、角度の小さい方で決めます。
Copyright© Digital Advantage Corp. All Rights Reserved.


 羽山博
羽山博