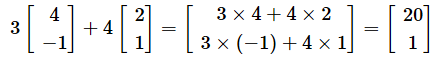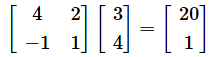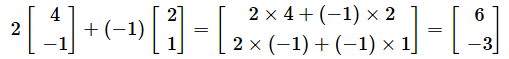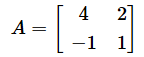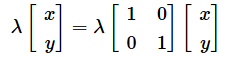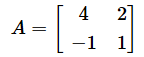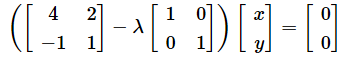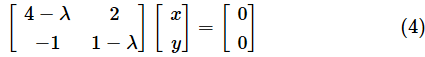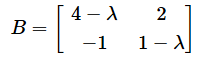［AI・機械学習の数学］線形代数の固有値・固有ベクトルをマスター：AI・機械学習の数学入門（1/3 ページ）

連載の通常の流れとは別の番外編。前回の行列式に続いて、今回は固有値と固有ベクトルについて、ポイントを押さえて見ていく。名付けて「挫折しない固有値・固有ベクトル」というお話（にするつもり）。統計学や機械学習のさまざまな手法の背景にあるこれらの考え方に触れてみよう。

[羽山博，著]

連載目次

　前回の番外編4では、図形的な意味や一次独立、一次従属といった線形代数の基本を踏まえて行列式について見てきました。今回も同様に、固有値と固有ベクトルの考え方について、ポイントを押さえながら説明します。また、行列の対角化を行うことにより、行列のべき乗を簡単に求める方法を紹介し、その応用としてマルコフ過程の事例を紹介します。

ポイント1　固有ベクトルは一次変換を行っても向きが変わらないベクトル

　ひと言でいうと、固有値や固有ベクトルは一次変換を特徴付ける値やベクトルです。しかし、以下のような式がいきなり登場して面食らってしまった人もいるのではないでしょうか。

　「一次変換を表す行列をAとしたとき、

を満たす0でないベクトルxをAの固有ベクトル、λを固有値と呼ぶ」

というものです。確かに、式を見た瞬間に気を失いそうになりますね。しかし、Aが行列で、λが定数であることに注目すれば、ベクトルを一次変換したものが、元のベクトルの定数倍になっている、つまり向きが変わらず長さだけが変わっているときに、等式が成り立つことが分かります。

　一次変換も、ベクトルの定数倍も図形的に表すことができるので、図形的に意味を考えてみましょう。まず、一次変換からです。

　番外編4でベクトルを移動させるお話をしました。番外編4とは少し違う例ですが、例えば、v₁＝(4,−1),v₂＝(2,1)を使えば、(3,4)を以下のように(20,1)に移すことができます。

　このような操作により、変換先が同じベクトル空間になるような変換を一次変換または線形変換と呼びます。v₁とv₂を縦に並べた行列にすれば、以下のように表すこともできます。この行列が一次変換を表す行列になります。

　一次変換は、基底を変えることによって座標を変換することと考えられます（図1）。これまで(1,0)と(0,1)を基に座標を決めていた（平面を構成していた）わけですが、(4,−1)と(2,1)を基に座標を決めることもできるというわけです。

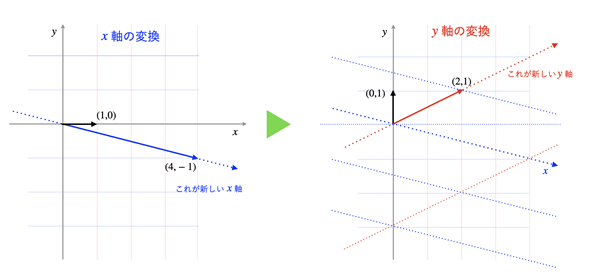図1　一次変換は座標を変換することとも考えられる
v₁＝(4,−1),v₂＝(2,1)による一次変換の場合。(4,−1)を新しいx軸とし、(2,1)を新しいy軸とした新しい座標を作成したものと考えられる。

　このとき、一次変換により、ベクトル(3,4)は(20,1)に移りました。これはあくまで元の座標での値です。これを新しい座標から見てみましょう（ここが大事です）。すると、元の座標の(20,1)は、新しい座標での(3,4)に当たることが分かります。平面（空間）をゆがめても、そのゆがんだ空間の中ではやはり(3,4)の位置であるというわけです。もし、自分の周りの空間そのものが（自分自身を含めて）突然ゆがんだとしても、その空間の中にいれば何の変化も感じられないはずです。しかし、外の世界から見ると、空間がゆがんでいることが分かります。それと同じようなことです。

　なお、元の座標の(3,4)は、新しい座標では(−0.83,3.17)に当たります。この計算は省略しますが、一次変換を表す行列の逆行列を(3,4)に掛ければ求められます。図2のように対応していることが分かります。

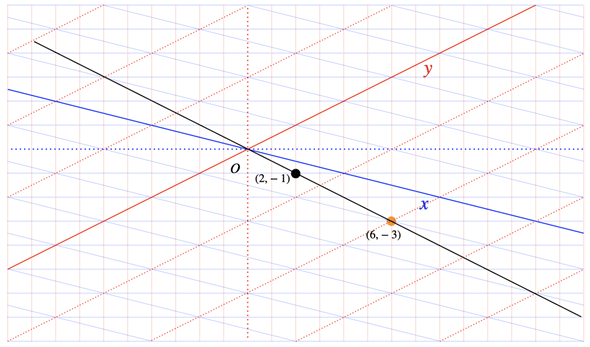
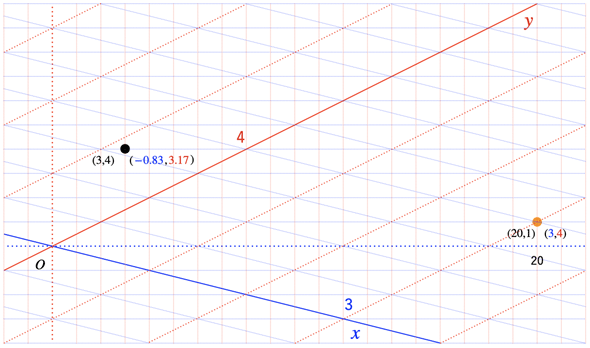図2　一次変換による座標の変換とベクトルの移動
一次変換により(3,4)は(20,1)に移動する。しかし、v₁＝(4,−1),v₂＝(2,1)を基底とした座標から見ると、やはり(3,4)の位置にあることが分かる。また、元の座標の(3,4)は、新しい座標での(−0.83,3.17)に当たる。ただし、ここでは細かな数値にこだわらなくても構わない。元の(3,4)が(20,1)という「原点Oから見て関係のない」位置に移動したということだけ確認しておくとよい。

　ところで、原点Oから見ると、元の(3,4)と移動先の(20,1)は全く関係のない位置にあるように見えます。しかし、ベクトルによっては、一次変換によって定数倍になるものもあります。例えば、(2,−1)を例に取ってみます。

となります。これは、元の(2,−1)を3倍したものです。元のベクトルを定数倍したものということは、同一直線上にあるということです。先ほどの(3,4)は、一次変換により（原点から引いた）異なる直線上に移りますが、(2,−1)は、一次変換により、元のベクトルと同一の直線上の点(6,−3)に移ります。

図3　一次変換によって同一直線上に移動するベクトルが固有ベクトル
一次変換によって、ベクトルが定数倍になった。図2と見比べて違いを確認しておこう。

　ここで、移動先のベクトルを求めるために掛けた値（3）が、一次変換

に対する固有値となり、(2,−1)というベクトルが固有ベクトルになります。なお、この例では、固有値と固有ベクトルの組はもう1つあり、固有値が2、それに対する固有ベクトルが(−1,1)となります*1。

*1　固有ベクトルは「向き」が同じであれば、長さはいくらであっても構いません。例として挙げた固有ベクトルを定数倍したものも固有ベクトルなので、同一直線上にあるベクトルは全て同じ固有ベクトルと見なせます。ここで「固有ベクトルはもう1つある」というのは向きが異なる固有ベクトルがもう1つあるという意味です（これについては後でまた触れます）。なお、一次変換のための配列によっては固有ベクトルが1つになる場合や、固有ベクトルが求められない場合もあります。

ポイント2　固有値の求め方（考え方を中心に）

　では、固有値の求め方を見ておきましょう。最初に示した以下の式から考えていきます。ポイント4で2×2行列の固有値を簡単に求める方法も紹介しますが、考え方を理解するために順を追って見ていきます。

　λがスカラーのままだと取り扱いにくいので、右辺も行列の積として表しましょう。右辺は以下のように表せます。Eは単位行列です。

　このことは、成分表示にするとよく分かります。2×2行列であれば以下のようになりますね。

　話を元に戻します。（1）式の右辺に（2）式の右辺を代入すれば、以下のようになります。

　右辺を左辺に移項しておきます。

xでくくれば以下のようになります。

　ここからは具体例で計算してみましょう。ポイント1で使った以下の2×2行列でやってみます。

　これを（3）式に代入してみましょう。

　()内を計算すると以下のようになります。

　この式をよーく見てください。今は固有ベクトルを探しているので、(x,y)は零（ゼロ）ベクトルでないものとします。従って、(x,y)に左から掛けている行列をBと表すと、

には逆行列が存在しません。もし、逆行列B⁻¹が存在するなら、B⁻¹B＝Eとなり、（4）式が

となってしまい、(x,y)は零ベクトルではないという前提と矛盾するからです。Bに逆行列が存在しないということは……そう、行列式の値が0になるということです！

　では、行列式を求めて、0と置いてみましょう。

という二次方程式になります。左辺を展開します。

　因数分解すると、

となるので、λ＝3とλ＝2であることが分かります。これで固有値が求められました。

　続いて固有ベクトル(x,y)を求めます。