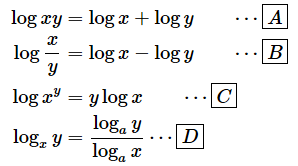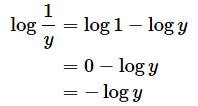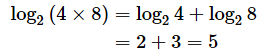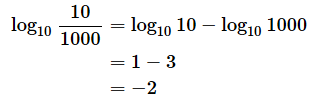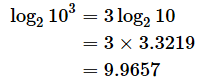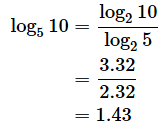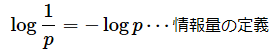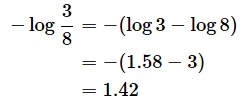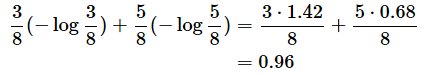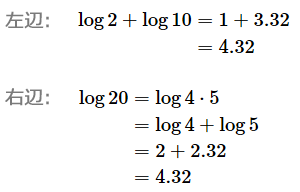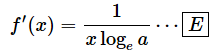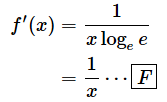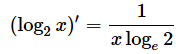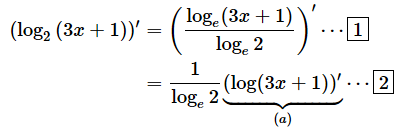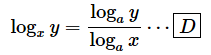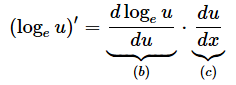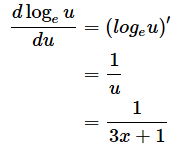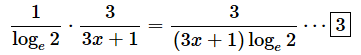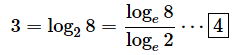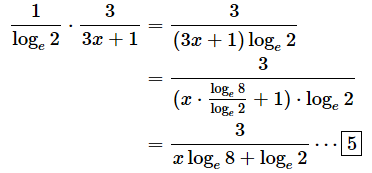[AI・機械学習の数学]指数と対数(対数編):AI・機械学習の数学入門
連載の通常の流れとは別の番外編。指数と切っても切れ離せない「対数」を解説。対数関数の性質や対数関数の微分法についても簡単に紹介する。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
この連載の本編では、微分やベクトル・行列などのいわば数学の「縦糸」にあたるテーマを取り上げていますが、番外編では、さまざまなテーマにまたがる、いわば「横糸」にあたるテーマを取り上げます。前回は「指数」を取り上げましたが、今回は指数と切っても切り離せない「対数」について見ていくこととします。
対数とは、端的にいえばある数の指数部分を取り出す計算です。対数を使えば、掛け算になっている式を足し算で表せるように変形できます。また、指数関数の値の対数を取れば、グラフが直線で表せます。まずは、対数の表し方から見ていきましょう。
ポイント1 対数の表し方
対数を理解するには、指数をきちんと理解しておく必要があります。おさらいをかねて、具体例で見てみましょう。23=8の意味をあらためて確認しておきます。図1の上半分を見てください。2は「底(てい)」でしたね。3はもちろん「指数」です。2の3乗が8になるというわけです。
では、図1の下半分に移ります。書き方を見ながら対数の意味を明らかにしていきましょう。対数を表すには、最初にlog(ログ)と書き、logの右下に小さく底を書きます。この場合であれば、底は2です。そして、その隣に「真数(しんすう)」と呼ばれる値を書きます。真数とは、底を何乗かした値のことです。この例だと、8が真数です。つまり、2を何乗かしたら8になるということです。
- log28 …… 2を何乗かしたら8になる、その「何乗か」を求める
答えはもちろん3ですが、これは、その「何乗か」という値のことですね。それが対数です。つまり、対数とは、底を決めたときに、真数を得るための指数はいくらであるかということです。図1を見れば、指数と対数は表裏一体の関係にあることが分かります。少し例を見ておきましょう。
(例1)
3を何乗したら81になるか……34=81なので、答えは4。
(例2)
2を何乗したら10になるか……2x=10を解けばx=3.3219...となります(この方程式は簡単には解けませんが23=8,24=16であることから、3と4の間の値であることは分かりますね)。
なお、底が10の対数(例えばlog1081など)のことを常用対数と呼び、底がeの対数(例えばloge81など)のことを自然対数と呼びます。特に底が指定されていない場合(例えばlog 81など)はeが底であるものと見なされます。ただし、底がeでない場合でも、文脈から底の値が明らかであるときには、底を省略して書くこともあります。
ポイント2 対数の性質や公式のまとめ
対数の意味が分かれば、以下の式の意味も簡単に分かると思います。
続いて、基本的な公式についてもまとめておきます。以下の公式は底が1以外の正の実数であれば成り立つので、底を省略しています。
[A] …… 掛け算は足し算になる(ただしx,yは正の実数)
[B] …… 割り算は引き算になる(ただしx,yは正の実数)
[C] …… べき乗はlogの外に出せる(ただしxは正の実数、yは実数)
[D] …… 底をaに変換する(x,y,aは正の数、x≠1,a≠1)
[B]式でxの値が1であれば、log x=0になるので、以下の式が成り立つことも分かります。
それぞれ、例を見ておきましょう。
(例3)
左辺は2を何乗したら32(=4×8)になるかということです。25=32なので答えは5です。右辺の計算と合っていますね。これは、指数に関する以下の公式に対応するものです。指数の部分だけを見ると同じ形になっていますね(a=2,m=2,n=3となります)。
(例4)
(例5)
例5では答えを小数点以下4桁まで求めています。既に例2でlog210=3.3219であることは見たので、その値を使いました。結果が整数にならない場合は手計算では難しいので、PythonやExcelなどの関数を使ってlog2103の値と3 log210を比べておきます。Pythonなら以下の通りです。
>>> import math
>>> math.log(10**3,2)
9.965784284662087
>>> 3*math.log(10,2)
9.965784284662089
最下位の値が異なるのは浮動小数点数の計算時に起こる誤差のため。数学的には等しい。
Excelなら、「=LOG(10^3,2)」と「=3*LOG(10,2)」を任意のセルに入力して結果を見比べるといいでしょう。
(例6)
ここでは、小数点以下第二位まで計算しました。log210=3.32...、log25=2.32...です。このように、底を変換すると、そのままでは計算しづらい場合でも、既知の値を使った計算にできることがあります。
対数の公式についてはこれぐらいにして、次に対数関数について見ていきます。が、その前にコラムを1つ挟んでおきましょう。以下のコラムは、これまでに見た公式を活用するので、対数の計算方法を確認するのにも役立ちます。
コラム 対数と情報量の表し方
情報量とは、平たくいうと「情報の価値」です。ある情報が得られたとき、それがまれにしか起こらないものだと、その情報の価値は高いと考えられます(いわば「スクープ」に当たりますね)。ということは、その事象が起こる確率pの小さい方が情報量は大きくなると考えられます。そこで、情報量の尺度として、以下のように確率pの逆数を取ることにします。pが小さくなると1/pは大きくなるからです。
この対数を取ると以下のようになります。なぜ対数を取るのかは後でお話することとして、これが情報量の定義です。底は2です。また、情報量の単位はビットです。
例えば、さまざまな身分のメンバー8人の中から学生を選びたいとき、学生が3人と分かった場合の情報量を求めてみましょう。無作為に選んだ人が学生である確率は3/8です。log23=1.58とすると、情報量は以下のように1.42ビットとなります。
なお、各々の情報量に確率を掛けた期待値のことを平均情報量(エントロピー)と呼びます。例えば、上の例で、学生である確率は3/8、学生でない確率は5/8なので、平均情報量は、log 3/8=1.42、log 5/8=0.68を利用して、
となります。全てが等確率であるときには平均情報量は最大(1)になり、情報に偏りがある場合には平均情報量は小さくなります。
さて、対数を取る理由ですが、それはズバリ、掛け算を足し算にして表したいからです。具体例で見てみます。例えば、1〜10までの数字が書かれた赤玉と白玉があるものとしましょう(全部で20個です)。この中で、どれが当たりであるか、ヒントを教えてもらえるものとしましょう。
- 情報A: 当たりは赤 → 確率は10/20=1/2、その逆数は2
- 情報B: 当たりは5番 → 確率は2/20=1/10、その逆数は10(こちらの価値が高い)
さらに以下のようにヒントが得られたものとします。
- 情報C: 当たりは赤の5番 → 確率は1/20、その逆数は20
これらの情報の価値には以下のような関係が成り立っていることが分かります(2×10=20ですね)。
情報量を取り扱うときには、「情報A+情報B=情報C」のように、掛け算ではなく足し算として表した方がスッキリするので、各項の対数を取ります。すると、
となります。このように、対数を使えば掛け算を足し算に変えられるというわけです。左辺と右辺をそれぞれ小数点以下第二位まで計算してみましょう。log 10=3.32、log 5=2.32です。
ちゃんと合っていますね。このことを情報量の加法性と呼びます。
ポイント3 対数関数の値とグラフ
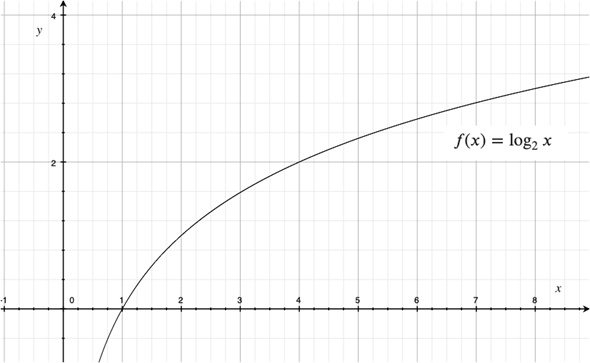
対数関数は、f(x)=logaxのように、対数を使って表された関数です。f(x)=log2xであれば、以下のような値を取ります。
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 対数関数 log2x | 0 | 1 | 1.58 | 2 | 2.32 | 2.58 | 2.81 | 3 | 3.17 | 3.32 |
| 表1 対数関数の値の変化 | ||||||||||
グラフも描いておきましょう。
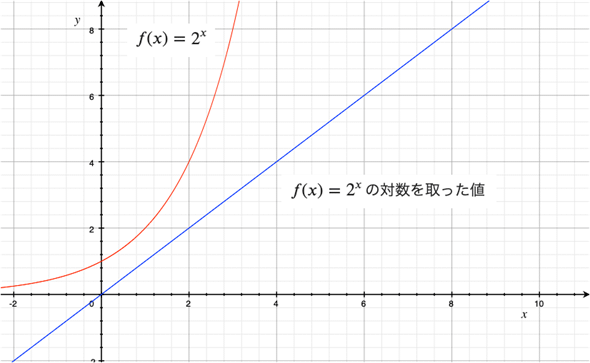
番外編2でも見たように、指数関数は急激に値が増えていきます。そのため、xが少し大きくなるだけですぐにグラフが上にはみ出してしまいます。そのような場合には対数を取ってグラフ化すると便利です。回帰式が指数関数になるようなデータの場合も、対数を取ると近似曲線が直線になるので、扱いやすくなります。以下に値の変化の様子と、グラフを示しておきます。
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 指数関数 2x | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
| 対数を取る | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
対数を取るということは、2xのxを求めるということなので、当然のことながら直線的な関係になる。
ポイント4 対数関数の微分
対数関数の微分法については、公式と計算例を記すにとどめます。計算例には、簡単な例と、公式をフル活用するちょっと難しめのものを含めておきます。
のとき、
となります。
f(x)の底がeのときは、
となります。
(例7)
これは、公式[E]を適用しただけで求められました。
最後に、多少複雑なものも紹介しておきましょう。本編の第8回で見た合成関数の微分を使います。ちょっと難しいので、すぐに理解できなくても問題はありませんが、少しずつでも慣れるようにするといいでしょう。
(例8)
[1]では、底をeにそろえました。これは公式[D]を使った変形です(下に再掲)。分母のloge2は定数なので、くくりだしたのが[2]の式です。
次に、[2]の(a)の部分で、3x+1=uと置き、連鎖律を使うと、
となります。(b)の部分は、公式[F]を使って微分できますね。
(c)の部分は、(3x+1)'=3となるので、結局、[2]式は、
となります。このままでも構わないのですが
であることを利用して、以下のように変形できます。
[5]では、分配法則を使って、loge2を x⋅loge8 / loge2 と 1 に掛けました。スッキリした形になりましたね。
今回は、対数の計算方法と対数関数、指数関数の微分法について整理しました。最後に、これまでに登場した公式の活用や本編で見た合成関数の微分などの計算方法を使いました。番外編としては、積分や線形代数のキーワードについても取り扱う予定なので、ご期待ください。
Copyright© Digital Advantage Corp. All Rights Reserved.

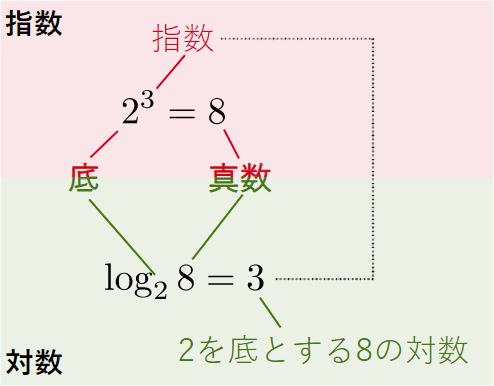 図1 指数と対数の関係
図1 指数と対数の関係