［評価指標］特異度（Specificity）とは？：AI・機械学習の用語辞典

用語「特異度」について説明。二値分類タスク（問題）に対する評価指標の一つで、実際の正解値が「陰性」で、かつ、予測値も「陰性」だった正解数（＝TN）を、実際の正解値が「陰性」である全てのデータ数（＝FP＋TN）で割った値を指す。

[一色政彦，デジタルアドバンテージ]

連載目次

用語解説

　統計学／機械学習における特異度（Specificity）とは、（基本的に）二値分類のタスク（問題）に対する評価指標の一つで、正解値（真の値）が「陰性（Negative、負例）」であるデータ全体のうち、機械学習モデルによる予測値も「陰性」で正解だった確率である。0.0（＝0％）〜1.0（＝100％）の範囲の値になり、1.0に近づくほどより良い。

　特異度の計算は、実際の正解値が「陰性」で、かつ、予測値も「陰性」だった正解数（＝TN）を、実際の正解値が「陰性」である全てのデータ数（＝FP＋TN）で割ることで計算できる（図1）。

図1　「特異度」のイメージ

　二値分類の混同行列を使ってあらためて計算式を書き出すと以下のようになる。

　特異度は、「陰性」の予測での取りこぼしをできるだけ少なくしたい場面で使いやすい評価指標である。

　感度（Sensitivity）と特異度はセットで理解しておくと分かりやすいので、両者の具体例を比較しておこう。

　例えば健康診断であれば、検査の感度（＝誤検出も含めた検出率）が高いほど好ましい。感度が高い状況では、病気である可能性のある人をできるだけ広く検出する。「少しでも問題がありそうであれば、精密検査を受けてもらう」という方が病気を見落とさない確率が高まるというメリットがある。

　一方、その精密検査であれば、今度は特異度が高いほど好ましい。特異度が高い状況では、病気ではない人（＝正解が陰性）が「病気だ（陽性）」と判定されることはめったにない、つまり「特異」なこととなる。もし、健康な人を誤って病気だと判定してしまう方が、医者としてリスクが大きいので、この方がよいのではないかと思われる。

　よって精密検査のケースでの評価指標としては、感度（「FN：偽陰性」の低さを重視した評価指標）よりも特異度（「FP：偽陽性」の低さを重視した評価指標）を採用する方が好ましいと考えられる。まとめると特異度は、実際の正解値が陰性のデータに対しては、機械学習モデルによる予測時に「陽性」と間違う不正解はできるだけ出したくない場合（＝陽性予測においては、できるだけ不正解を出したくない場合）に使えばよい。

　なお、「FP：偽陽性」の低さを重視した評価指標という特徴が適合率（Precision）と特異度で同じなので、両者は「別方向から見た同類の評価指標」と言えるだろう。

感度と特異度のトレードオフ

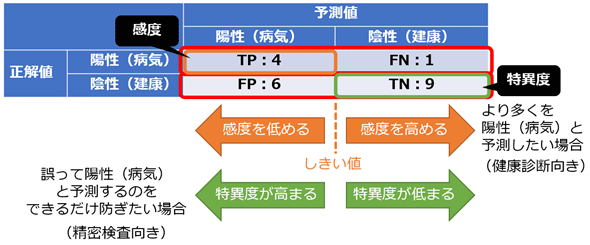
　ここまでの説明で分かると思うが、感度と特異度は基本的にトレードオフの関係にあり、通常、感度を高めると特異度が低くなり、特異度を高めると今度は感度が低くなる（図2）。

図2　感度と特異度のトレードオフ

　例えば感度を高くするために、より多くの予測値（範囲は0.0〜1.0とする）が陽性（1.0）になるよう、分類判定のしきい値を中央の0.5から0.3に変更したとする。これにより確かに「真陽性（TP）」が増えて感度は高まるが、「真陰性（TN）の数」は減って特異度が低まることになる。逆に感度を低くすると、特異度は高まる可能性が高い。

「AI・機械学習の用語辞典」