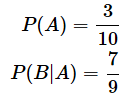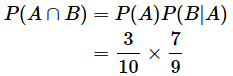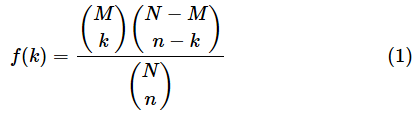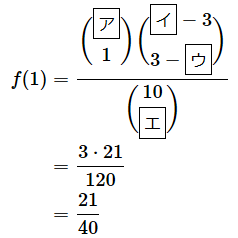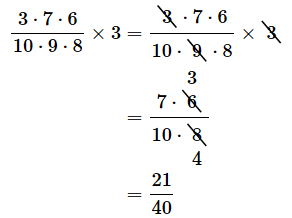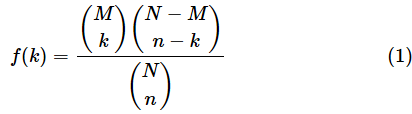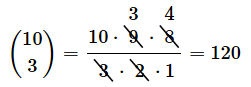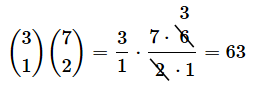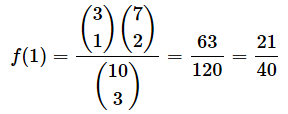［データ分析］超幾何分布 〜 くじ引き（非復元抽出）の確率を求める！：やさしい確率分布
データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載（確率分布編）の第3回。まず「非復元抽出（例：くじ引き）とは何か」を説明。その確率分布である超幾何分布を取り上げ、その意味や特徴などを解説します。
連載：
この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』連載（記述統計と回帰分析編）の続編で、確率分布に焦点を当てています。
この確率分布編では、推測統計の基礎となるさまざまな確率分布の特徴や応用例を説明します。身近に使える表計算ソフト（Microsoft ExcelやGoogleスプレッドシート）を使いながら具体的に事例を見ていきます。
必要に応じて、Pythonのプログラムや統計ソフト「R」などでの作成例にも触れることにします。
数学などの前提知識は特に問いません。中学・高校の教科書レベルの数式が登場するかもしれませんが、必要に応じて説明を付け加えるのでご心配なく。肩の力を抜いてぜひとも気楽に読み進めてください。
羽山博筆者紹介： IT系ライターの傍ら、非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。趣味の献血は心拍数が基準を超えてしまい99回で中断。心肺機能を高めるために水泳を始めるも、一向に上達せず。また、リターンライダーとして何十年ぶりかに大型バイクにまたがるも、やはり体力不足を痛感。足腰を鍛えるために最近は四股を踏む日々。超安全運転なので、原付やチャリに抜かされることもしばしば（すり抜けキケン、制限速度守ってね！）。
データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の確率分布編、第3回です。前回は離散分布の基礎としてベルヌーイ分布と二項分布を取り上げました。今回は「非復元抽出とは何か」をお話しした後、その確率分布である超幾何分布を取り上げ、その意味や特徴などを見ていきます。
温泉旅行が何本か当選する確率を求めるには？
商店街の福引（ふくびき）で、1等の温泉旅行にチャレンジする光景を思い浮かべてみてください。手元にある福引券3枚と交換に「ガラガラ」を3回、回したとき、1等を1本引く確率を求めてみたいと思います。
ガラガラは「ガラポン」とも呼びます。機種にもよりますが、2000〜3000個の玉が入るものが多いようです。なお、正式名称は「新井式回転抽出機」だそうです。
この例は、コイン投げやサイコロ、あるいは前回の記事で見たヒットが出る確率と決定的に異なる点があります。それはいったい何でしょうか。図1を見ながら、違いを考えてみてください。
ここでは、話を分かりやすくするため、1等の温泉旅行が10本中3本あるものとします。つまり、ガラガラには玉が10個入っていて、当たりが3個あるというわけです。実際にはそんなに当たりやすい福引はありませんが、ヒットが出る確率と比較しやすい値としました。その場合に、3回のチャレンジのうち、1等を1本引く確率を考えます。
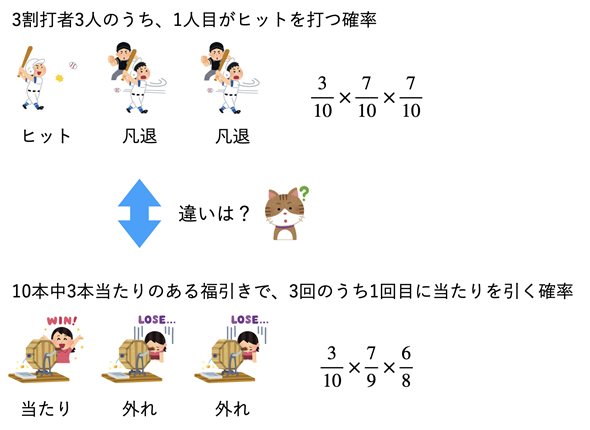図1 復元抽出と非復元抽出（3人の打者がヒットを1本打つ確率と、3回の福引で1等を1本引く確率の違い）違いを分かりやすくするため、それぞれの確率を分数で表してある。ヒットが出る確率は常に3/10（10分の3）。しかし、福引の場合は前の試行で当たりが出たかどうかによって次の確率が変わる。図には、1本目がヒット（当たり）の確率だけを示している。実際には、2本目がヒット（当たり）の場合と3本目がヒット（当たり）の場合もある。それらの場合も含めた確率については後述する。
野球の例では、それぞれの打者がヒットを打つかどうかは独立であるという前提でした。つまり、前の打者がヒットであっても、凡退であっても、次の打者がヒットを打つ確率は3/10＝0.3、凡退する確率は7/10＝0.7となります。
しかし、福引の場合は、ガラガラを回すたびに玉が1つずつ減っていきます。前回の試行で当たりが出たか、外れが出たかによって、次の試行で当たりが出る確率が変わります。例えば、最初が当たりである確率は3/10＝0.3ですが、次は玉が1つ減るので全体は9個となり、当たりも2個に減ります。外れは相変わらず7個のままです。その場合、2番目の玉が当たりである確率は2/9で、外れである確率は7/9です。このように、前の試行の結果が次の試行の確率に影響するような場合を従属と呼びます。
野球の例は、例えば赤玉が3個、白玉が7個の合計10個の玉が入っている壺（つぼ）から玉を取り出した後、取り出した玉を元に戻す場合と同じです。玉の総数も赤玉と白玉の個数も変わりません。このような取り出し方を復元抽出と呼びます。
一方、福引の例は、取り出した玉を元に戻さない場合と同じです。玉を取り出すたびに玉の個数は1つずつ減っていきます。また、赤玉を取り出せば赤玉の個数が減り、白玉を取り出せば白玉の個数が減ります。このような取り出し方を非復元抽出と呼びます。
コラム 条件付き確率とは
このコラムは、話の流れから少し外れるので、先に進みたい方は読み飛ばしていただいても構いません。
福引の例では、1回目で当たりを引いた後に外れを引く確率と、1回目で外れを引いた後にまた外れを引く確率は異なりますね。「1回目に当たりを引く」という事象をAと表し、「2回目に外れを引く」という事象をBと表すと、1回目に当たりを引いたという条件の下で、2回目に外れを引く確率はP(B|A)と表わされます。このP(B|A)は条件付き確率と呼ばれます。
条件付き確率については、以下の式（条件付き確率の乗法公式）が成り立ちます。
- P(A∩B) …… 1回目に当たりを引き、かつ2回目に外れを引く確率（1回目と2回目の両方を満たす確率のこと）
- P(B|A)…… 1回目に当たりを引いた場合に、2回目に外れを引く確率（2回目の確率のこと）
図1の1回目と2回目だけを取り上げると、以下のようになります。
なので、
となり、図1の福引きの例で見た最初の2回に当てはまります。
条件付き確率の乗法公式はベイズ統計学の出発点となる公式です。詳細については、［AI・機械学習の数学］機械学習でよく使われる「ベイズの定理」を理解するをご参照ください。
超幾何分布は非復元抽出の確率分布
では、福引の例で、3回のうち1回当たりを引く確率を求めてみます。図1では1本目が当たりの例を見ましたが、2本目が当たりの場合と、3本目が当たりの場合もあります。
非復元抽出で、総数がN個、総数のうちの成功数がM回、試行回数がn回、試行のうちの成功数がk回の場合の確率分布を超幾何分布（ちょうきかぶんぷ、Hypergeometric distribution）と呼びます。最初に超幾何分布の公式を示しておきます。確率変数が取る値をkとします。後で具体的な例を見ながら超幾何分布の意味を解きほぐしていくので、公式が理解できなくても気にせず先に進めてください（計算についても、後述するExcelのHYPGEOM.DIST関数を使えば簡単にできます）。
この式にある( )は、ベクトルや行列ではなく、組み合わせ数を表します。計算方法については、前回の記事で説明しましたので、忘れた場合はそちらを復習してください。
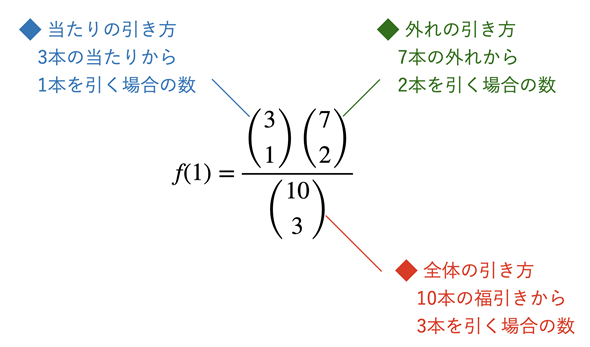
まずは、N、M、n、kが、福引の例でどの値に当たるかを確認しておきましょう。オレンジ色の部分をクリックまたはタップすると答えが表示されます。
| 値 | 意味 | 福引の例での値は？ |
|---|---|---|
| N | 総数 | 10 |
| M | 総数のうちの成功数 | 3 ← 1等の玉の個数 |
| n | 試行回数 | 3 ← 何回ガラガラを回せるか |
| k | 試行のうちの成功数 | 1 ← 1等の玉が出た個数 |
（1）式に値を当てはめると、当たりが1本出る確率が求められます（図1で見た1本目が当たりの場合だけでなく、2本目が当たりの場合、3本目が当たりの場合も含めた確率です）。( )で表す組み合わせ数の計算方法は後で説明します。ここでは計算結果だけを確かめてください。
答え： ア＝ 3 、イ＝ 10 、ウ＝ 1 、エ＝ 3
取りあえず確率は求められました。ここからは福引の例を具体的に見ながら、上の結果と一致することを確認します。また、上の公式の意味についても、あらためて説明します。
すでに述べたように、図1で見たのは3回の試行のうち、1回目に当たりを引く確率でした。3回の試行のうち、当たりを1本引くのは、2回目に当たりを引く場合と、3回目に当たりを引く場合があります。これらを全て図にしてみましょう（図2）。
図2 10本中3本の当たりがある福引に3回チャレンジして当たりを1本引く確率1回チャレンジするたびにガラガラの玉が1つずつ減っていくので、分母は10×9×8。当たりを引くと当たりの玉が減り、外れを引くと外れの玉が減るので、分子は3（当たりの場合の数）と7×6（外れの場合の数）を掛けたものになる。それらが3通りあるので、後述する式で確率が求められる。
いずれの場合も、分母は10×9×8で、分子は（掛け算の順序は異なりますが）3×7×6です。3通りの場合があるので、求める確率は以下のようになります。
公式で求めた結果と一致しましたね。ここであらためて公式を確認しておきましょう。
福引の例のN＝10, M＝3, n＝3, k＝1を当てはめて、意味を見てみます（図3）。N−M＝10−3＝7, n−k＝3−1＝2です。
図3の式を計算してみましょう。分母は以下のようになります。
分子は以下のようになります。
従って、f(1)の値は以下のようになり、図2での計算と一致しますね。
超幾何分布の確率質量関数と累積分布関数を可視化してみよう
ここまでは、当たりを1本引く確率しか見てきませんでした。つまり、確率変数の値k＝1の場合だけでした。福引の例であれば、全て外れ（k＝0）から、3本とも当たり（k＝3）の場合までがあるので、それらの確率を全て求め、確率質量関数と累積分布関数を可視化してみましょう。
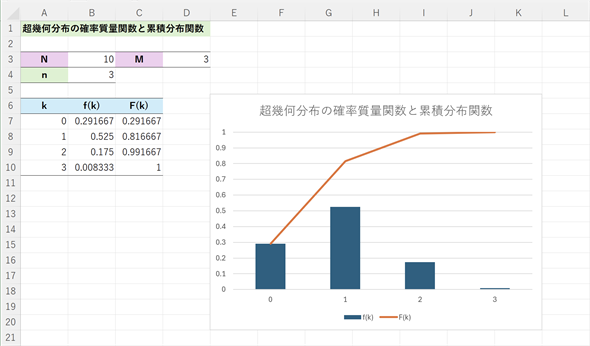
（1）式を使って計算することもできますが、ExcelのHYPGEOM.DIST関数を使えば簡単です。結果は図4のようになります。グラフ作成の手順は図4の後に記しておきます。
グラフ作成の手順は以下の通りです。サンプルファイルをこちらからダウンロードし、［超幾何分布］ワークシートを開いて試してみてください。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから［ファイル］−［コピーを作成］を選択し、Googleドライブにコピーしてお使いください。なお、GoogleスプレッドシートのHYPEGEOM.DIST関数には最後の引数がない（確率質量関数の値しか求められない）ことに注意が必要です。具体的な操作方法は、サンプルファイル内に記載しています。
◆ Excelでの操作方法
- セルB7に=HYPGEOM.DIST(A7:A10,B4,D3,B3,FALSE)と入力する
- 古いバージョンのExcelでスピル機能が使えない場合は、あらかじめ結果が求められるセル範囲（セルB7〜B10）を選択しておき、関数を入力した後、入力の終了時に［Ctrl］＋［Shift］＋［Enter］キーを押す
- セルC7に=HYPGEOM.DIST(A7:A10,B4,D3,B3,TRUE)と入力する
- 古いバージョンのExcelでスピル機能が使えない場合は、あらかじめ結果が求められるセル範囲（セルC7〜C10）を選択しておき、関数を入力した後、入力の終了時に［Ctrl］＋［Shift］＋［Enter］キーを押す
- セルB6〜C10を選択する
- ［挿入］タブを開き、［複合グラフの挿入］ボタンをクリックして［集合縦棒 - 折れ線］を選択する
- ［グラフのデザイン］タブを開き、［データの選択］ボタンをクリックする
- ［データソースの選択］ダイアログボックスで［横（項目）軸ラベル］の下の［編集］ボタンをクリックする
- ［軸ラベル］ダイアログボックスで［軸ラベルの範囲］ボックスをクリックし、セルA7〜A10を選択する
- ［OK］をクリックして［軸ラベル］ダイアログボックスを閉じる
- ［OK］をクリックして［データソースの選択］ダイアログボックスを閉じる
HYPEGEOM.DIST関数の引数は図5のように指定します。母集団とは集団全体のことで、福引の例で言えば、ガラガラの中に入っている玉全体のことです。標本とは母集団から取り出したもののことです。図5には、超幾何分布の確率質量関数の公式も併せて示してあるので、対応を確認しておいてください。
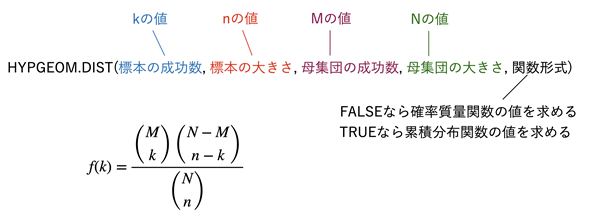図5 HYPGEOM.DIST関数に指定する引数図4の例では、標本の成功数（kに当たる値＝目的の事象が起こる回数）としてA7:A10というセル範囲を指定しているので、スピル機能によりセルA7〜A10の成功数に対する確率質量関数の値や累積分布関数の値が一度に求められる。Excelのヘルプには、2番目の引数が「標本数」と記されているが、標本数という用語は、標本の抽出を何回行ったかを表したり、標本が何種類あるか（グループの数）を表したりするのに使われるので、誤解のないように「標本の大きさ」とした。
なお、サンプルファイルには、（1）式に従って確率質量関数と累積分布関数の値を求めた例も含めてあります。興味のある方はご参照ください。
二項分布と超幾何分布
二項分布と超幾何分布の違いは、復元抽出であるか非復元抽出であるかということです。母集団が大きくなると二項分布と超幾何分布の値はほぼ等しくなります。例えば、100万本のくじから1本引いたとしても、残りの数はほとんど変わらないからです（残りは99万9999本ですね）。サンプルファイルには当たりが30本ある100本のくじを10回引いたときの、二項分布と超幾何分布のf(0)〜f(10)の値を求め、グラフを描いた例を含めてあります（図6）。N＝100でもかなり近い値になっていることが分かります。
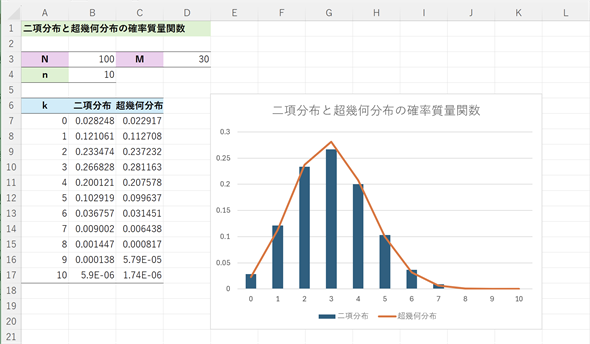図6 Nの値が大きいときの二項分布と超幾何分布二項分布の確率質量関数を棒グラフで、超幾何分布の確率質量関数を折れ線グラフで描いてみた。N＝100の場合でも、二項分布と超幾何分布がほぼ重なることが分かる。
今回は、非復元抽出の確率分布として超幾何分布を取り上げました。超幾何分布はここで見た例の確率を求めるだけでなく、データの件数が少ない場合の独立性の検定などにも使われます。これらのことについても、いずれ紹介したいと思います。
さて、次回は、離散型確率分布の別の例として、まれにしか起こらない事象の確率を求めるために使われるポアソン分布を取り上げます。次回もお楽しみに！
この記事で取り上げた関数の形式
関数の利用例については、この記事の中で紹介している通りです。ここでは、今回取り上げた関数の基本的な機能と引数の指定方法だけを示しておきます。
超幾何分布の確率質量関数や累積分布関数の値を求めるための関数
HYPGEOM.DIST関数： 超幾何分布の確率質量関数や累積分布関数の値を求める
形式
HYPGEOM.DIST(標本の成功数, 標本の大きさ, 母集団の成功数, 母集団の大きさ, 関数形式)
引数
- 標本の成功数： 標本の中で目的の事象が起こる数を指定する。
- 標本の大きさ： 母集団から取り出した標本の数（試行の総数）を指定する。
- 母集団の成功数： 母集団の中での目的の事象が起こる数を指定する。
- 母集団の大きさ： 母集団全体の数を指定する。
- 関数形式： 以下の値を指定する。
- FALSE …… 標本の成功数に対する確率質量関数の値を求める
- TRUE …… 標本の成功数までの累積分布関数の値を求める
「やさしい確率分布」
Copyright© Digital Advantage Corp. All Rights Reserved.
注目のテーマ
ITmediaはアイティメディア株式会社の登録商標です。