ジャッカード類似度（Jaccard Similarity）／ジャッカード係数（Jaccard Index）とは？：AI・機械学習の用語辞典

用語「ジャッカード類似度」について説明。集合間の類似性を評価する尺度で、「2つの集合がどれだけ重なり合っているか」（＝全体の要素数に対する共通部分の割合）を測定するために使用される。値が1に近いほど「似ている」を、0に近いほど「似ていない」を意味する。主にクラスタリングや文書比較などで利用されている。

» 2024年09月09日 05時00分公開

[一色政彦，デジタルアドバンテージ]

連載目次

用語解説

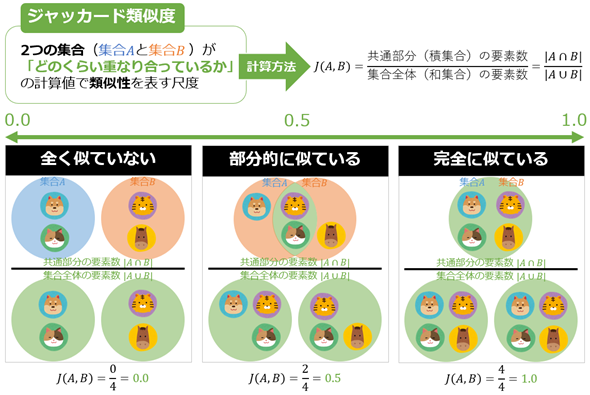
　数学／統計学／機械学習におけるジャッカード類似度（Jaccard Similarity）とは、2つの集合が「どのくらい重なり合っているか」の計算値で類似性を表す尺度である。具体的には、「2つの集合の共通部分（＝積集合：∩）」に含まれる要素数を、「2つの集合全体（＝和集合：∪）」に含まれる要素数で割ることで計算される（図1）。このジャッカード類似度の値は、0～1の範囲に正規化され、1なら「完全に同じ集合（＝似ている）」、0なら「全く共通点のない集合（＝似ていない）」を意味する。

図1　ジャッカード類似度のイメージ

　ジャッカード類似度は、ジャッカード係数（Jaccard Indexや、Jaccard similarity coefficient）とも呼ばれる。これらの用語は同じ概念を指しており、文脈によって使い分けられる。一般的に、Jaccard Similarityは類似度の強調や実際の応用で使われることが多く、Jaccard Indexは統計的な解析や数学的な文脈で使用されることが多い。また、「ジャッカード」ではなく「ジャカード」と表記される場合もある。

　また、1からジャッカード係数を引くことで非類似度（dissimilarity、言い換えると「距離」）を測定する指標にジャッカード距離（Jaccard distance）がある。ジャッカード距離は、ジャッカード類似度と同じような用途で逆の指標として使える、と考えるとよいだろう。

定義と数式

　すでに図1と冒頭の解説で計算方法に言及しているが、あらためて数式としてまとめ、計算例を示しておく。

　この2つの集合のジャッカード類似度、すなわち「この2つの集合がどれだけ重なり合っているか」を求める数式は、以下のように表される。なお、∩という数学記号は「集合の共通部分」（＝積集合：「かつ」と同じ意味）を、∪は「集合全体」（＝和集合：「または」と同じ意味）を表す。

　つまり、|A ∩ B|は「集合Aと集合Bの共通部分」に含まれる要素数を表し、|A ∪ B|は「集合Aと集合Bの両方（＝集合全体）」に含まれる要素数を表す。この数式によって計算されるジャッカード類似度の値は、先ほども説明した通りに0～1の範囲に収まるようになる。

　例えば、集合Aが{1, 2, 3}、集合Bが{2, 3, 4}である場合、A ∩ Bは{2, 3}であり、A ∪ Bは{1, 2, 3, 4}である。従って、この場合のジャッカード類似度は、以下の計算で0.5となる。

　この結果は、「集合Aと集合Bが半分程度、似ている」ことを意味する。つまり、2つの集合は「似ている」とも「似ていない」とも言えない中間的な状態にある。

　前述した通り、ジャッカード類似度は、値が1に近いほど類似しており、0に近いほど類似していないことを示す。ただし、中間的な値については、具体的な解釈が状況によって異なるため、目的に応じて柔軟に判断することが重要である。

　前掲の図1の例も同様に説明すると、以下のようになる。

集合Aが{犬, 猫}、集合Bが{虎, 馬}である場合、A∩Bは{ }であり、A∪Bは{犬, 虎, 猫, 馬}となり、ジャッカード類似度は0.0である。
集合Aが{犬, 虎, 猫}、集合Bが{虎, 猫, 馬}である場合、A∩Bは{虎, 猫}であり、A∪Bは{犬, 虎, 猫, 馬}となり、ジャッカード類似度は0.5である。
集合Aが{犬, 虎, 猫, 馬}、集合Bが{犬, 虎, 猫, 馬}である場合、A∩Bは{犬, 虎, 猫, 馬}であり、A∪Bは{犬, 虎, 猫, 馬}となり、ジャッカード類似度は1.0である。

用途

　ジャッカード類似度は、主にクラスタリング（例：図1のような「動物のグループ分け」）や、文書比較、レコメンデーション（推薦）システムなどで広く利用されている。

　例えば、文書比較では、各文書を単語の集合として捉え、その集合間のジャッカード類似度を計算することで、文書同士の類似度を評価できる。レコメンデーションシステムでは、ユーザーの行動を集合として表現し、その集合間の類似度を計算することで、似た行動を取るユーザーに対して、似たコンテンツを推薦することが可能となる。

　この他、ジャッカード類似度は画像や音声の分析、ゲノムデータの解析など、データが集合として表現されるさまざまな分野で利用されている。

API

　ジャッカード類似度は、主要ライブラリにおける以下のクラス／関数で定義されている。

scikit-learn： jaccard_score関数
PyTorch：基本ライブラリには含まれない。高レベルAPIのPyTorch LightningライブラリにはJaccardIndexクラスがあり、高レベルAPIのPyTorch IgniteライブラリにはJaccardIndexクラスがある

【応用】IoU（Intersection over Union）との関係

　ちなみに、画像セグメンテーションタスクの評価指標であるIoU（Intersection over Union）の計算には、ジャッカード係数と同じ計算式を用いる。具体的には、「予測された領域」と「実際の領域」の間で「どれだけ重なり合っているか」（＝「予測領域と正解領域で共通の面積」÷「2つの領域全体の面積」で算出する割合）を測定して評価する指標である。そのため、IoUは「ジャッカード係数（Jaccard Index）」と呼ばれることがある。

「AI・機械学習の用語辞典」