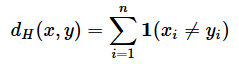ハミング距離（Hamming distance）とは？：AI・機械学習の用語辞典

用語「ハミング距離」について説明。同じ長さの2つの系列（文字列やビット列）を比較して、異なる位置の数をカウントすることで、2系列間の距離（または類似度）を計測する方法。エラーチェックやデータ比較、クラスタリングに利用され、データ間の違いや類似度を直感的に評価できる。

[一色政彦，デジタルアドバンテージ]

印刷

通知 連載「％」の新着をメールで通知

隕九ｋPost

Shareシェア

はてなブックマーク

SharePocket Button

連載目次

用語解説

　情報理論／機械学習／自然言語処理におけるハミング距離（Hamming distance）とは、同じ長さの2つの系列（文字列やビット列など）間の「異なる位置の数」をカウントすることで、「距離」を計算する方法である。例えば、

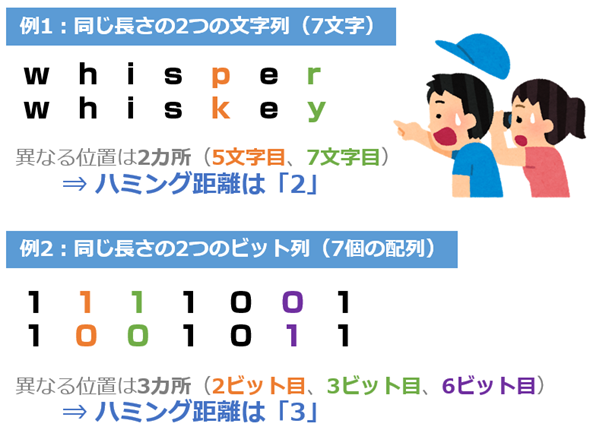
• whisper
• whiskey

という2つの文字列間のハミング距離は2である。また、例えば、

• 1111001
• 1001011

というビット列間のハミング距離は3だ。計算方法は、同じ長さの2つの文字列やビット列を比較して、異なる箇所を数えるだけである（図1）。

図1　ハミング距離のイメージ

　※ここでの長さn個のビット列は数学的な概念であり、通常は単純に0と1の配列として扱われる。このビット列には、コンピュータのハードウェアやプログラミングなどで見られる上位ビットや下位ビットといった概念は含まれないので注意してほしい。

定義と数式

　系列xと系列yのハミング距離を求める数式は、以下のように定義できる。nは「系列（文字列やビット列など）の長さ」とする。

　この数式における1(x_i ≠ y_i)は、条件（x_i ≠ y_i）が真の場合は1、偽の場合は0を返す関数（指示関数）である。つまり、系列xとyの各位置iにおいて、異なる場合に1をカウントし、合計することでハミング距離を求めている。

使い所と注意点

　ハミング距離は、以下のような場面で活用できる。

• エラーチェック： 例えば、データ転送時のエラーを検出して訂正する「ハミング符号」などに利用。
• データ比較： 例えば、同じ長さの2つの文字列やバイナリデータ、遺伝子のDNAシーケンスで類似度を測定するのに使用。
• クラスタリング： 例えば、ビット列データに対するクラスタリングで、距離を計算するのに使用。センサーデータの状態をビット列で表現することで、似た状態をグループ化（＝クラスタリング）する場合など。

　このようにハミング距離は、幅広い分野で利用されている。ただし、機械学習や自然言語処理、データサイエンスの分野では、必ず学ぶ基礎知識ではあるものの、ハミング距離を利用する機会は少ないかもしれない。現実には、より高度な「レーベンシュタイン距離（編集距離）」（後日解説予定）や「コサイン類似度」などを使うことが多いだろう。

【応用】レーベンシュタイン距離との関係

　ハミング距離と同様に、2つの系列（文字列）間の距離を測定する方法にレーベンシュタイン距離（別名：編集距離）がある。ハミング距離は「レーベンシュタイン距離の一種」とも言え、「レーベンシュタイン距離の特殊なケース」として捉えられている。

　大きな違いは適用範囲にある。レーベンシュタイン距離が長さの異なる系列（文字列）間にも適用できるのに対し、ハミング距離は同じ長さの系列（文字列）にしか適用できない。さらに、レーベンシュタイン距離は「挿入」「削除」「置換」の3つの操作を考慮して系列を変換するが、ハミング距離は「置換」のみを対象とする。このため、ハミング距離はより制限された状況下で使われるが、特定の用途では簡便に利用できる。

「AI・機械学習の用語辞典」

鬯ｩ謳ｾ�ｽ�ｵ�ｽ�ｽ�ｽ�ｺ鬯ｮ�ｦ�ｽ�ｮ髯ｷ�ｻ�ｽ�ｻ�ｽ�ｽ�ｽ�ｿ�ｽ�ｽ�ｽ�ｽ鬯ｯ�ｯ�ｽ�ｨ�ｽ�ｽ�ｽ�ｾ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�｣鬯ｯ�ｮ�ｽ�ｴ髣費ｿｽ�ｽ�･�ｽ�ｽ�ｽ�ｳ�ｽ�ｽ�ｽ�ｨ�ｽ�ｽ�ｽ�ｽ髯懶ｽ｣�ｽ�､�ｽ�ｽ�ｽ�ｸ�ｽ�ｽ�ｽ�ｲ鬯ｩ蠅捺��ｽ�ｿ�ｽ�ｽ�ｽ縺､ﾂ€�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�｣鬯ｯ�ｮ�ｽ�ｴ鬯ｩ蟶壽桶�ｽ�ｭ鬮ｮ�｣�ｽ�ｿ�ｽ�ｽ�ｽ�ｽ�ｽ�ｨ鬮ｯ蛹ｺ�ｻ繧托ｽｽ�ｿ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｺ鬮｣蛹�ｽｽ�ｵ髫ｴ謫ｾ�ｽ�ｴ�ｽ�ｽ隶難ｽ｣�守｢托ｽｭ雜｣�ｽ�｢�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｩ鬯ｩ蟷｢�ｽ�｢髫ｴ雜｣�ｽ�｢�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｼ鬯ｩ蟷｢�ｽ�｢髫ｴ荳ｻ�ｽ隶捺ｻゑｽｿ�ｽ邵ｺ�､�つ€鬯ｯ�ｮ�ｽ�ｦ�ｽ�ｽ�ｽ�ｪ鬩包ｽｶ闔ｨ�ｽ�ｽ�ｦ�ｽ�ｴ�ｽ縺､ﾂ€髯ｷ闌ｨ�ｽ�ｷ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｻ鬯ｯ�ｯ�ｽ�ｪ�ｽ�ｽ�ｽ�ｭ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｲ鬯ｩ謳ｾ�ｽ�ｵ�ｽ�ｽ�ｽ�ｺ鬮ｯ�ｷ�ｽ�ｷ�ｽ�ｽ�ｽ�ｶ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ New

ここを更新しました（2024年9月9日）

2024年9月9日：「【応用】レーベンシュタイン距離との関係」を追記しました。

AI・データサイエンスの学びをここから

初心者向け、データ分析・AI・機械学習・Pythonの勉強方法　＠ITのDeep Insiderで学ぼう