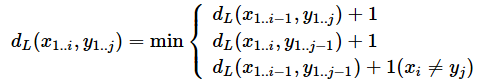レーベンシュタイン距離（Levenshtein distance）／編集距離とは？：AI・機械学習の用語辞典

用語「レーベンシュタイン距離」について説明。2つの系列（文字列やDNA配列など）を比較して、一方から他方へ変換するのに最も少ない編集操作（挿入／削除／置換）の回数をカウントすることで、2系列間の距離を計測する方法。文章の編集作業量の計測、スペルチェック、データクリーニング、DNA配列の比較などに利用され、データ間の違いや類似度を評価できる。

[一色政彦，デジタルアドバンテージ]

連載目次

用語解説

　情報理論／機械学習／自然言語処理におけるレーベンシュタイン距離（Levenshtein distance）とは、2つの系列（文字列やDNA配列など）間で片方からもう片方への「編集操作の最小回数」をカウントすることで、「距離」を計算する方法である。この編集操作には、

• 削除： 1文字を削除する
• 挿入： 1文字を追加する
• 置換： 1文字を別の文字に置き換える

の3つが含まれる。このため、レーベンシュタイン距離は編集距離（Edit distance）とも呼ばれる。

図1　レーベンシュタイン距離のイメージ

　例えば、

• 「おはようございます。」という文字列から
• 「おはやいですね。」という文字列へ

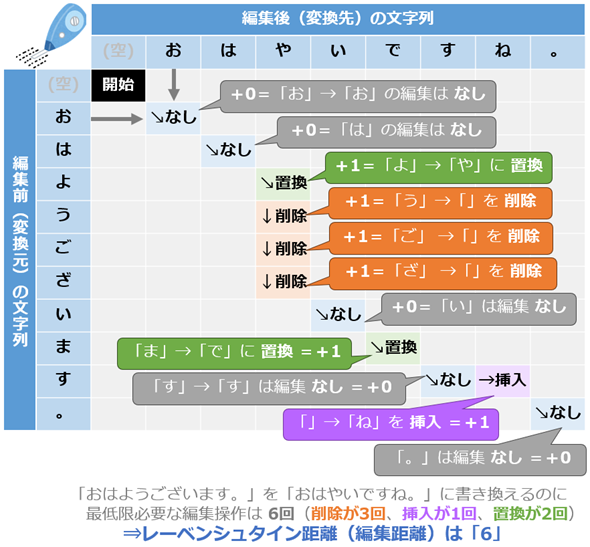
編集する場合のレーベンシュタイン距離は6となる。これは、下記の6回の編集操作によって「おはようございます。」を「おはやいですね。」に変換できるからだ（図1）。

1. 変更なし： お
2. 変更なし： は
3. 置換： よ → や
4. 削除： う
5. 削除： ご
6. 削除： ざ
7. 変更なし: い
8. 置換： ま → で
9. 変更なし： す
10. 挿入： ね
11. 変更なし： 。

　図1は、編集前の文字列を行に取り、編集後の文字列を列に取った表である。レーベンシュタイン距離の計算には、一般的に動的計画法によるアルゴリズムが用いられる。動的計画法（DP：Dynamic Programming）とは、大きな問題を小さな部分問題に分解し、それらの解を組み合わせて最終的な解を求める手法である。レーベンシュタイン距離の計算では、先頭に（空）文字列のセルを置くため、長さn文字と長さm文字の場合は、n＋1行m＋1列の二次元行列の表を作成し、その各セルで部分問題を解いていく。図1では「なし」「削除」「挿入」「置換」がセルに書かれているが、実際には各セルにおけるレーベンシュタイン距離が記入される（図2）。

　そして、この表の一番右下にあるセルの数値が、2つの文字列間での「最小回数の編集操作」を計算したレーベンシュタイン距離となる。ここだけ計算すればよさそうなものだが、これを計算するには、それまでに計算したセルの値を使う必要があるため、結局は一番左上のセルから計算を始めて、表内の全てのセルにおけるレーベンシュタイン距離を計算してくことになる。計算が大量になるので、通常は手計算ではなくプログラミングによって処理する方が効率が良い。

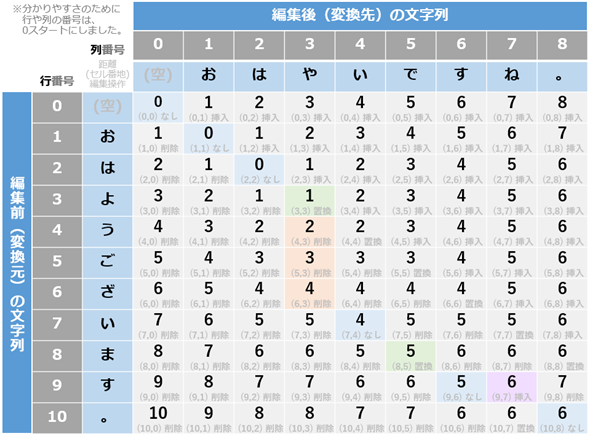
　図2は、実際に表内の全セルでレーベンシュタイン距離を計算した結果だ（ちなみに、これらの数値はPythonプログラムによって計算した。Pythonによるレーベンシュタイン距離の計算方法は後述する）。

図2　表内の全セルでレーベンシュタイン距離を計算した結果

　図2の表の作り方を説明する。

計算方法と数式

　まず数学やプログラミングで表現しやすいように、2つの文字列をxとyと表現することにしよう。

• 系列x： おはようございます。
• 系列y： おはやいですね。

　図2のように、n＋1行m＋1列の表を作成したら、表の0行目と0列目を初期化する（※行番号と列番号は0からスタートした方が計算結果と一致して分かりやすいので、最初の行と列を「0行目」と「0列目」と表現している）。

• 0行目： （空）文字列からyの部分文字列への距離
  • セル(0,0)： （空） → （空） ＝ 0【変更なし】
  • セル(0,1)： （空） → （空）お ＝ 1【挿入】（＝「お」が挿入された）
  • セル(0,2)： （空） → （空）おは ＝ 2【挿入】（＝「おは」が挿入された）
  • セル(0,3)： （空） → （空）おはや ＝ 3【挿入】
  • セル(0,4)： （空） → （空）おはやい ＝ 4【挿入】
  • セル(0,5)： （空） → （空）おはやいで ＝ 5【挿入】
  • セル(0,6)： （空） → （空）おはやいです ＝ 6【挿入】
  • セル(0,7)： （空） → （空）おはやいですね ＝ 7【挿入】
  • セル(0,8)： （空） → （空）おはやいですね。 ＝ 8【挿入】

　【挿入】とあるのは、左のセルよりも1文字挿入したということ。1セルで1操作なので1つずつカウントアップしている。

• 0列目： xの部分文字列から（空）文字列への距離
  • セル(0,0)： （空） → （空） ＝ 0【変更なし】
  • セル(1,0)： （空）お → （空） ＝ 1【削除】（＝「お」が削除された）
  • セル(2,0)： （空）おは → （空） ＝ 2【削除】（＝「おは」が削除された）
  • セル(3,0)： （空）おはよ → （空） ＝ 3【削除】
  • セル(4,0)： （空）おはよう → （空） ＝ 4【削除】
  • セル(5,0)： （空）おはようご → （空） ＝ 5【削除】
  • セル(6,0)： （空）おはようござ → （空） ＝ 6【削除】
  • セル(7,0)： （空）おはようござい → （空） ＝ 7【削除】
  • セル(8,0)： （空）おはようございま → （空） ＝ 8【削除】
  • セル(9,0)： （空）おはようございます → （空） ＝ 9【削除】
  • セル(10,0)： （空）おはようございます。 → （空） ＝ 10【削除】

　【削除】とあるのは、上のセルよりも1文字削除したということ。1セルで1操作なので1つずつカウントアップしている。

　以上で初期化が済んだので、次に各文字列で構成された行列の各セルで計算していく。計算方法は、以下のルールに従う。

• 文字が同じ場合：
  • 【変更なし】： 左上のセルの値を引き継ぐ（つまり同じ数値）。
• 文字が異なる場合： 以下の編集操作のうち、最小のコストになるものを選択する。
  • 【削除】： 上のセルの値に1を足す。
  • 【挿入】： 左のセルの値に1を足す。
  • 【置換】： 左上のセルの値に1を足す。

　実は、上記の0行目の【挿入】や0列目【削除】も同じルールで計算されている。

　例えば、以下のように計算できる。対象のセルまでの計算結果を踏まえた上で、対象セルの計算を加算（＋0か＋1か）していることに注意してほしい。

• セル(1,1)： お＝お …… 文字が同じ場合
  • 左上のセル(0,0)の値「0」＋0【変更なし：左上のセルの値を引き継ぐ】＝0
• セル(1,2)： お≠は …… 文字が異なる場合
  • 左のセル(1,1)の値「0」＋1【挿入：左のセルの値に1を足す】＝1
• セル(3,3)： よ≠や …… 文字が異なる場合
  • 左上のセル(2,2)の値「0」＋1【置換：左上のセルの値に1を足す】＝1
• セル(4,3)： う≠や …… 文字が異なる場合
  • 上のセル(3,3)の値「1」＋1【削除：上のセルの値に1を足す】＝2

　各セルの計算を確かめやすいように図2を再掲する。

図2（再掲）　表内の全セルでレーベンシュタイン距離を計算した結果

　念のため見方を丁寧に説明すると、例えばセル(4,3)は、以下の3つの編集コストが選択肢となる。

• 【削除】： 上のセル(3,3)の値「1」に1を足す＝2
• 【挿入】： 左のセル(4,2)の値「2」に1を足す＝3
• 【置換】： 左上のセル(3,2)の値「1」に1を足す＝2

　この場合、【削除】と【置換】が2で、【挿入】が3なので、最小コストは2である。【削除】か【置換】のいずれかで処理すればよい。距離は同じなので、どちらでも構わない。筆者が作成したプログラムでは、【削除】【挿入】【置換】の順で処理したので、【削除】が選択されている。

　以上で説明した「各セルにおける計算ルール」を数式で表現すると次のようになる。iは現在の行番号で、jは現在の列番号だ。

　これで以下の意味になる。

• 【削除】： 上のセル(i−1, j)の値に1を足す。
• 【挿入】： 左のセル(i, j−1)の値に1を足す。
• 【置換】： 左上のセル(i−1, j−1)の値に1を足す（文字が異なる場合）。
  • 【変更なし】： 左上のセル(i−1, j−1)の値を引き継ぐ（文字が同じ場合）。

　この数式における1(x_i ≠ y_j)は、条件（x_i ≠ y_j）が真の場合は1、偽の場合は0を返す関数（指示関数）である。つまり、比較している2つの文字が異なる（例えばセル(4,3)なら「う」と「や」で異なる）場合にのみ1を足すことを意味する。

使い所と注意点

　レーベンシュタイン距離は、以下のような場面で活用できる。

• 編集作業量の計測： 文章を加筆修正した際に、どれくらい編集したかを数値化するのに利用。
• データクリーニング： スペルミスやタイプミスにより微妙に異なる類似する文字列を発見して1つに統合するのに利用。
• スペルチェック： 単語のスペルが間違っているかを確認し、正しいスペルを提案するのに利用。
• DNA配列の比較： 遺伝子シーケンスの類似度を測定するのに利用。

　このようにレーベンシュタイン距離は、幅広い分野で利用されている。ただし、計算量が多いため、大規模データに対しては注意が必要である。

Pythonプログラムの実装例

　レーベンシュタイン距離を計算するには、先ほどのルールをプログラムに落とし込むだけである。とはいえ、手軽にコピー＆ペーストで試したいだろう。そこで、筆者が（ChatGPTを使って）書いたサンプルコードを最後に示しておく。コード内容は説明はしないので、必要があれば、本稿の説明と比べながら自分で読み解いてほしい。Google Colabのscratchpadにコードを入力すれば手軽に試せる。

import numpy as np
import pandas as pd

def levenshtein_distance_matrix(x, y):
    # 表を作成
    n, m = len(x), len(y)
    dp = np.zeros((n + 1, m + 1), dtype=int)

    # 初期化
    for j in range(m + 1):
        dp[0][j] = j
    for i in range(n + 1):
        dp[i][0] = i

    # 各セルで計算していく
    for i in range(1, n + 1):
        for j in range(1, m + 1):
            if x[i - 1] == y[j - 1]:
                dp[i][j] = dp[i - 1][j - 1]           # 【変更なし】
            else:
                dp[i][j] = min(dp[i - 1][j] + 1,      # 【削除】
                               dp[i][j - 1] + 1,      # 【挿入】
                               dp[i - 1][j - 1] + 1)  # 【置換】

    # 逆方向にたどって操作を記録（この部分は検証用で、実際には不要）
    steps = []
    i, j = n, m
    while i > 0 or j > 0:
        if i > 0 and j > 0 and x[i - 1] == y[j - 1]:
            steps.append(f"変更なし: {x[i - 1]}")
            i -= 1
            j -= 1
        elif i > 0 and (j == 0 or dp[i][j] == dp[i - 1][j] + 1):
            steps.append(f"削除: {x[i - 1]}")
            i -= 1
        elif j > 0 and (i == 0 or dp[i][j] == dp[i][j - 1] + 1):
            steps.append(f"挿入: {y[j - 1]}")
            j -= 1
        else:
            steps.append(f"置換: {x[i - 1]} → {y[j - 1]}")
            i -= 1
            j -= 1

    return dp[n][m], steps[::-1], dp

# 「おはようございます。」と「おはやいですね。」の編集距離と手順を計算
x = "おはようございます。"
y = "おはやいですね。"
distance, steps, matrix = levenshtein_distance_matrix(x, y)

print("レーベンシュタイン距離:")
print(distance)
print("\n操作手順:")
for step in steps:
    print(step)
print("\n距離の計算行列:")
matrix_df = pd.DataFrame(matrix, index=[""] + list(x), columns=[""] + list(y))
print(matrix_df)

# レーベンシュタイン距離:
# 6

# 操作手順:
# 変更なし: お
# 変更なし: は
# 置換: よ → や
# 削除: う
# 削除: ご
# 削除: ざ
# 変更なし: い
# 置換: ま → で
# 変更なし: す
# 挿入: ね
# 変更なし: 。

# 距離の計算行列:
#         お は や い で す ね 。
#      0  1  2  3  4  5  6  7  8
# お   1  0  1  2  3  4  5  6  7
# は   2  1  0  1  2  3  4  5  6
# よ   3  2  1  1  2  3  4  5  6
# う   4  3  2  2  2  3  4  5  6
# ご   5  4  3  3  3  3  4  5  6
# ざ   6  5  4  4  4  4  4  5  6
# い   7  6  5  5  4  5  5  5  6
# ま   8  7  6  6  5  5  6  6  6
# す   9  8  7  7  6  6  5  6  7
# 。  10  9  8  8  7  7  6  6  6

リスト1　レーベンシュタイン距離を計算するPythonサンプルコード

【応用】ハミング距離との関係

　レーベンシュタイン距離と同様に、2つの系列（文字列）間の距離を測定する方法にハミング距離がある。レーベンシュタイン距離は、「ハミング距離の一般化」と見なせる。

　具体的には、適用範囲が広がっているという点で一般化されている。ハミング距離が同じ長さの系列（文字列）にのみ適用可能なのに対し、レーベンシュタイン距離は長さの異なる系列（文字列）間にも適用できる。さらに、ハミング距離は「置換」のみを対象として系列を変換するが、レーベンシュタイン距離では「挿入」「削除」「置換」の3つの操作を考慮する。そのため、レーベンシュタイン距離はより柔軟で幅広い状況に対応できる。

「AI・機械学習の用語辞典」

ここを更新しました（2024年9月9日）

2024年9月9日：「【応用】ハミング距離との関係」を追記しました。

AI・データサイエンスの学びをここから

初心者向け、データ分析・AI・機械学習・Pythonの勉強方法　＠ITのDeep Insiderで学ぼう