「正則化」手法(ラッソ回帰、リッジ回帰)をPythonで学ぼう:機械学習入門
「知識ゼロから学べる」をモットーにした機械学習入門連載の第4回。過学習を抑えて予測精度を向上させるための「正則化」手法として、ラッソ回帰とリッジ回帰に注目。その概要と仕組みを図解で学び、Pythonとscikit-learnライブラリを使った実装と正則化の効果も体験します。初心者でも安心! 易しい内容です。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
前回(第3回)では、売上予測など「データの傾向を把握して、数値を予測する」際に役立つ、機械学習の代表的な手法である線形回帰について学びました。この予測精度を「もっと高めたい」とは思いませんか?
モデルを評価した結果、予測精度、つまり機械学習モデルの性能があまり良くなかったとします。原因として、過剰適合(過学習)の可能性が考えられる場合、過剰適合を減らすための手法である正則化(Regularization)を試してみる価値があります。そこで今回は、ラッソ回帰とリッジ回帰という正則化手法について学んでいきましょう。
具体的には、ラッソ回帰やリッジ回帰の概要から、その仕組み、そしてPythonプログラミングによる回帰モデルの実装と評価まで、正則化手法の基礎スキルを短時間で習得することを目指します(図1)。これにより、線形回帰モデルの性能を改善するテクニックの一つが身に付きます。
ただし、正則化によって必ずしも機械学習モデルの性能が向上するわけではありません。「性能が向上する可能性があるから、まずは試してみる」という姿勢が大切です。もし向上しなかった場合には、決定木回帰やニューラルネットワーク回帰といった他の機械学習手法に切り替えて、さまざまな手法を試してみることをお勧めします。
第2回では、Pythonを使った機械学習プログラミングの基本的な流れを、実際にコードを書きながら体験的に学びました。よって本稿では、共通する内容説明はできるだけ省略し、大事なエッセンスに集中することにします。線形回帰に特有の説明も基本的に省略するので、必要に応じて前回の再読をお勧めします。
今回で学べること
ラッソ回帰やリッジ回帰といった正則化手法は、線形回帰だけでなく、ニューラルネットワークなどでも役立つため、「実務で機械学習を使いたい人なら必ず習得しておきたいスキル」の一つです。「線形回帰の次に学ぶべき手法」と言えます。
図1の通り、正則化手法をプログラミングにより実現するには、第1回で紹介したPythonライブラリ「scikit-learn」が便利です。そこで本稿では、ラッソ回帰とリッジ回帰の概念を図解で説明した後、実際にscikit-learnを使ったプログラミングを体験します。実践で役立つ基本的な使用例に絞った内容です。
まとめると、今回は図2に示す内容を学ぶことができます。
それでは、まずはラッソ回帰とリッジ回帰の概要紹介から始めていきます。
連載:
「機械学習は難しそう」と思っていませんか? 心配は要りません。この連載では、「知識ゼロから学べる」をモットーに、機械学習の基礎と各手法を図解と簡潔な説明で分かりやすく解説します。Pythonを使った実践演習もありますので、自分の手を動かすことで実用的なスキルを身に付けられます。
本連載では、具体的な機械学習の手法(例:線形回帰、決定木、k-meansなど)を解説しています。次回以降の新着記事を見逃さないように、ぜひ以下のメール通知の登録をお願いします。
何の役に立つ手法?
あらためて説明すると、正則化(Regularization)とは、機械学習モデルが“訓練データ”に「過剰に適合してしまうこと」(=過学習)を防ぐためのテクニック(手法)です。過剰適合しているモデルでは、「“未知の新しいデータ”(例:テストセット)に対する予測精度」(=汎化性能)が悪化する問題が生じます。
正則化は、モデルの“複雑さ”を抑えることで、この問題を解決します。具体的には、モデルの各パラメーター値(例:線形回帰モデルの各係数)を制御し特徴量(説明変数)を抑制することで、モデルの“複雑さ”を抑えます(図3)。これにより過剰適合が抑制されて、汎化性能が改善することが期待できます。
正則化には幾つかの方法がありますが、線形回帰やニューラルネットワークなどで使える代表的なものにラッソ回帰とリッジ回帰があります。今回はこれらについてそれぞれ説明していきます。
ラッソ回帰やリッジ回帰の利用シーンは、線形回帰と同じです。例えば、不動産価格や売上などの数値予測に活用できます(冒頭の図1にも記載しています)。
ラッソ回帰(L1正則化)
ラッソ回帰(Lasso Regression)は、モデルの“複雑さ”を抑えるために、モデル内の各パラメーター値(例:回帰分析の場合は係数)を抑制し、一部を0にして不要な特徴量を取り除く手法です(前掲の図3)。重要な特徴量だけを残せるため、“ターゲット(目的変数)と関係性の薄い”特徴量が多いデータセットで特に効果を発揮します。
なお、ラッソ回帰で各パラメーター値を抑制する仕組みは、L1正則化とも呼ばれます。具体的には、パラメーターの「絶対値の合計」をペナルティーとして加え、これによって各パラメーター値を抑制します。この仕組みについては、後ほど詳しく説明します。
リッジ回帰(L2正則化)
リッジ回帰(Ridge Regression)は、モデルの“複雑さ”を抑えるために、モデル内の全てのパラメーター値(例:回帰分析の場合は係数)をバランス良く小さくする手法です(図4)。全ての特徴量を活用できるため、“ターゲットに寄与する”特徴量が多いデータセットで特に効果を発揮します。
リッジ回帰は、ラッソ回帰とは異なり不要な特徴量を排除せず、情報を失うことなくほぼ全ての特徴量を活用できるため、多くの特徴量をバランス良く生かしたい場合に適しています。また、特徴量同士で強い相関が見られる場合、つまり多重共線性が疑われる場合にも、それを抑制するのに有効です。
なお、リッジ回帰で各パラメーター値を抑制する仕組みは、L2正則化とも呼ばれます。具体的には、パラメーターの「2乗値の合計」(=二乗和)をペナルティーとして加え、これによって各パラメーター値を抑制します。この仕組みを、次に詳しく解説します。
どんな仕組み?
先ほども述べましたが、ラッソ回帰やリッジ回帰では、L1正則化やL2正則化と呼ばれる手法により、モデルの各パラメーターを調整して特徴量を抑制します。以下で、その仕組みをできるだけ数式ではなく図解を中心に説明していきます。
ただし前提として、線形回帰の仕組み、具体的には最小二乗法を理解しておく必要があります。覚えていない場合は、前回の解説を読み返すことをお勧めします。
【前提知識】残差の二乗和(RSS)とは?
線形回帰では、最小二乗法という仕組みにより、「残差の二乗和(RSS:Residual Sum of Squares)」が最小となる最適なパラメーターを決定します。RSSの数式は以下の通りです(前回からの再掲です)。数式内のnはデータ数です。
機械学習や統計学では、モデルの各パラメーター(例:係数や切片)を自動的に決定(=最適化)するために最小化を目指す対象/目的(Object)となる値(実際には数学的な関数)は、目的関数(Objective function)と呼ばれます。具体的には、通常の線形回帰では、RSSが目的関数として使用されます。
正則化項とは?
一方、ラッソ回帰やリッジ回帰では、このRSSに「モデルの“複雑さ”を抑えるためのペナルティー(制約)」となる正則化項(regularization term)を追加したものを目的関数とします(図5)。この目的関数を最小化することで、特徴量を抑制する正則化を実現します。
では、「どのような正則化項を追加するのか」を見ていきましょう。ラッソ回帰の場合とリッジ回帰の場合について、それぞれ説明します。
ラッソ回帰の正則化項
ラッソ回帰の正則化項の数式は以下の通りです。この数式の意味、つまり「この正則化項がどのような効果をもたらすか」は後述するので、数式が苦手でも気にせずに読み進めてください。
数式内のpは特徴量の数、αは正則化の強さ、βjはj番目の特徴量に対応する係数を表します。ただし、切片β0は正則化項に含まれない点に注意してください。
この数式では、モデルの各パラメーター値(特徴量にかかる係数)の絶対値を合計しています。この計算内容は、L1ノルムと呼ばれる距離計算と同じです。そのためラッソ回帰はL1正則化とも呼ばれます。
なお、正則化項では、αというハイパーパラメーターで「正則化の強さ」を制御します。α値が大きいほど、正則化が強まり、より多くの特徴量が抑制される可能性があります。α値の決め方は、後述のコラムを参照してください。
以上の「正則化項」の数式を「RSS+正則化項」という目的関数の数式に代入すると、図6のようになります。
ペナルティーを課す正則化項を追加することで、特にラッソ回帰では「不要な特徴量の係数が0になる」効果が得られます。この効果は絶対値の特性に由来しますが、リッジ回帰と比較すると「ラッソ回帰がどのような効果をもたらすか」が明確になるので、後ほど「効果の違い」としてまとめて説明します。次にリッジ回帰の正則化項を見てみましょう。
リッジ回帰の正則化項
リッジ回帰の正則化項の数式は以下の通りです。こちらも「この正則化項がどのような効果をもたらすか」は後述するので、数式が苦手でも気にせずに読み進めてください。
先ほどと同じ説明になりますが、数式内のpは特徴量の数、αは正則化の強さ、βjはj番目の特徴量に対応する係数を表します。ただし、切片β0は正則化項に含まれない点に注意してください。
この数式では、モデルの各パラメーター値の2乗値を合計しています。この計算内容は、L2ノルムと呼ばれる距離計算とほぼ同じです。そのためリッジ回帰はL2正則化とも呼ばれます。ただし、L2ノルムでは二乗和の平方根(√)を取るのに対し、L2正則化では取らない、という違いもあるので注意してください。
以上の「正則化項」の数式を「RSS+正則化項」という目的関数の数式に代入すると、図7のようになります。
ペナルティーを課す正則化項を追加することで、特にリッジ回帰では「全ての特徴量の係数をバランス良く小さくする」効果が得られます。この効果は2乗値の特性に由来しますが、ラッソ回帰と比較すると「リッジ回帰がどのような効果をもたらすか」が明確になるので、「効果の違い」として次に詳しく説明します。
ラッソ回帰とリッジ回帰がもたらす効果の違い
数式を比較すると、ラッソ回帰では|βj|(絶対値)がペナルティーとして使われる一方で、リッジ回帰ではβj2(2乗値)が用いられています。この違いが、それぞれの正則化の効果に違いを生み出します。
そこで、絶対値と2乗値の特性を比較するため、横軸に各パラメーター値(係数)βjを、縦軸にペナルティー値(|βj|またはβj2)を取ったグラフを描いてみます。図8の左側に描かれた青色の線が絶対値のグラフ、右側に描かれたオレンジ色の線が2乗値のグラフです。
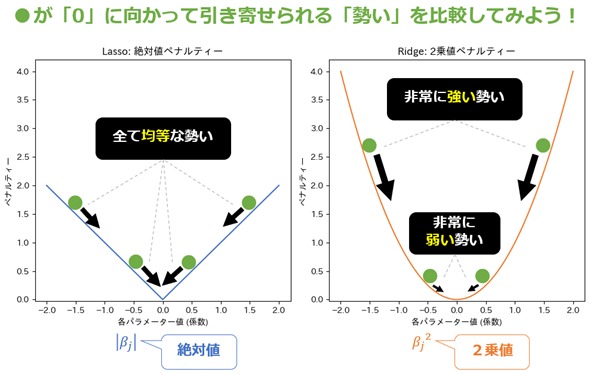 図8 仕組みの理解: 絶対値と2乗値の特性を比較
図8 仕組みの理解: 絶対値と2乗値の特性を比較各グラフの描画に当たり、βjの値を-2.0〜2.0の範囲で0.04間隔で設定しました(合計101点)。左側の絶対値のグラフは、これらの値を|βj|に入力した結果の各点を線で結んだものです。同様に、右側の2乗値のグラフは、βj2に入力した結果の各点を線で結んだものです。
ここで、丸いボールをイメージしてください(図8の●)。図8では、「目的関数を最小化する」処理を、ボール●が線グラフ上を転がりながら、最も低い0の地点を目指す動きで表現しています。
この動きの中で、ボール●が0に向かって引き寄せられる「勢い」は、曲線の傾斜(=線の傾き)によって決まります。傾斜が急な部分では勢いが強く、緩やかな部分では勢いが弱くなります。
絶対値の場合、βjの値がどのような値であっても傾斜の角度は一定です。つまり「全て均等な勢い」で0に向けて引き寄せられます(図8左)。このため、非常に簡単に0に収束します。これにより、ラッソ回帰では「不要な特徴量の係数が0になる」効果が得られます。
一方、2乗値の場合、βjの値が0から遠いほど傾斜が急で、近いほど緩やかになります。つまり0から遠いほど「非常に強い勢い」で、近いほど「非常に弱い勢い」で0に向けて引き寄せられます(図8右)。
これにより、リッジ回帰では「全ての特徴量の係数をバランス良く小さくする」効果が得られます。ただし、0に近づくほど勢いが弱くなり、係数が完全に0に収束することはほとんどありません。よって、ラッソ回帰のように不要な特徴量を排除することもなく、全ての特徴量を活用する形になります。
【コラム】正則化項の「α」値の決め方
正則化項のαについて詳しく説明します(αは前掲の図6や図7を参照)。既に説明した通り、αは、「正則化の強さ」を制御するためのハイパーパラメーター(=学習前に人間が指定する設定項目)です。
ここで、「αにどのような値を指定すればよいか?」という疑問を持つかもしれません。結論としては、データセットやモデルによって適切な値は異なるため、一概には言えません。ただし、一般的には0.0001〜10.0の範囲が候補になります。初期値としては0.1あたりから試すとよいでしょう。
α値を大きくすると、正則化項のペナルティーが強まります。図8の「曲線の傾斜」がより急になるイメージです。この結果、ラッソ回帰では、より多くの特徴量の係数が0となり、特徴量が排除されます。一方で、α値が大き過ぎると、必要な特徴量まで排除され、モデルの予測精度が低下する可能性があります。
また、α値が小さ過ぎる場合、正則化の効果がほとんど得られず、「過剰適合を防ぐ」という目的が達成できなくなる可能性があります。そのため、適切な範囲でα値を調整することが重要です。
実際には、モデルの予測精度を見ながらα値を調整(チューニング)します。手動調整の場合、値を少しずつ変更してラッソ回帰やリッジ回帰を何度も実行し、最適なα値を探ります。
ただし、この作業は手間がかかるため、scikit-learnのGridSearchCVクラスなどを使った自動調整が一般的です。GridSearchCVでは、あらかじめ設定した複数のα値をモデルに適用し、予測精度を比較して最適な値を自動的に見つけることができます。具体的な使用方法については後述の【発展】で説明します。
関連として、特徴量が大幅に削減されたモデルは、「スパース(sparse、疎)」と呼ばれます。スパースモデルは、不要な情報が少なく、コンパクトな構造が特徴です。これにより、モデルの解釈性が高まり、計算コストも削減できます。
ラッソ回帰やリッジ回帰では、特徴量の値のスケール(単位)がそろっていることが重要です。そろっていないと、例えば0.001と100.0などの係数が混在することになり、正則化が適切に機能しません。また、αの調整も難しくなります。
そのため、特にこれらの手法を使う際は、データセットを標準化(もしくは正規化)しておく必要があります。標準化は、各特徴量で平均を「0」に、標準偏差を「1」のスケールに変換する手法です。
以上でラッソ回帰モデルとリッジ回帰モデルが正則化を実現する仕組みを理解しました。続いて実践として、scikit-learnによるプログラミングを体験してみましょう。
体験してみよう
scikit-learnには、ラッソ回帰モデルを構築できるLassoクラスと、リッジ回帰モデルを構築できるRidgeクラス(いずれもsklearn.linear_modelモジュール)があります。使い方はほぼ同じなので、2つまとめて説明します。
LassoクラスとRidgeクラスの使い方
Lasso/Ridgeクラスをインスタンス化(例:modelオブジェクトを作成)したら、訓練セットで訓練をするfit()メソッドを呼び出すだけです(リスト1)。訓練された線形回帰モデルを使って予測(predict)するには、predict()メソッドを使います。
from sklearn.linear_model import Lasso, Ridge
lasso_model = Lasso()
ridge_model = Ridge()
lasso_model.fit(<特徴量:X>, <ターゲット:y>)
ridge_model.fit(<特徴量:X>, <ターゲット:y>)
lasso_model.predict(<新しいデータ>)
ridge_model.predict(<新しいデータ>)
もちろんLassoクラスやRidgeクラスには、これ以外の機能も備わっています。詳しくはLassoクラスの公式ページとRidgeの公式ページを参照してください。
それでは、これらのクラスを使って、実際にラッソ回帰モデルとリッジ回帰モデルを作成し、正則化の効果を確認してみましょう。
ノートブックの利用について
本連載は、第1回で説明したように、無料のクラウド環境「Google Colab」の利用を前提としています。基本的には、Colabで新規ノートブックを作って、以降で説明するコードを入力しながら実行結果を自分の目で確かめてください。既に入力済みのノートブックを使いたい場合は、こちらのサンプルノートブックをご利用ください。
実際に使ってみよう: データセットの作成
まずはデータセットを準備する必要があります。今回は、自作の独自データセットを使用します。scikit-learnには、回帰問題用の独自データセットを作成するためのmake_regression()関数があるので、これを用います。
前回は「California Housing(カリフォルニア住宅価格)データセット」を使ったのに、なぜ同じデータセットを使わないのかを疑問に思った人もいるかもしれません。
使わなかった理由は、California Housingデータセットでは正則化(L1およびL2)がモデルの性能に与える効果を十分に示せなかったためです。今回作成したデータセットは正則化の効果が明確に分かるよう工夫されています。
make_regression()関数(sklearn.datasetsモジュール)の詳細な使い方については、本稿のテーマとは直接関係がないため説明を割愛します。興味がある方は、公式ドキュメントをご参照ください。
独自のデータセットを作成してから、訓練セットとテストセットに分割するまでのコードを、以下のリスト2に示します。なお、データセットの前処理として標準化や正規化を忘れずに実施してほしいため、明確に標準化の実装コードも含めています。
from sklearn.datasets import make_regression
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
# 独自のデータセットを作成
data, target = make_regression(
n_samples=500, # データ数。この例では500個を生成
n_features=6, # 特徴量の数。この例では6つ作成
n_informative=4, # ターゲット値に影響を与える特徴量の数
noise=1.0, # ターゲット値に追加するノイズの標準偏差
effective_rank=1, # 値が小さいほど特徴量間の多重共線性が強くなる
random_state=0 # 乱数のシード値。再現性のために指定
)
# 特徴量とターゲットの取得
X = data
y = target
# データの標準化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 訓練セットとテストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.1, random_state=0)
print(f'訓練セットのサイズ: {X_train.shape}') # 訓練セットのサイズ: (450, 6)
print(f'テストセットのサイズ: {X_test.shape}') # テストセットのサイズ: (50, 6)
リスト2のmake_regression()関数では、6つの特徴量(説明変数、列)を持つ500個のサンプル(行)からなるデータセット(表形式データ)を生成しています。
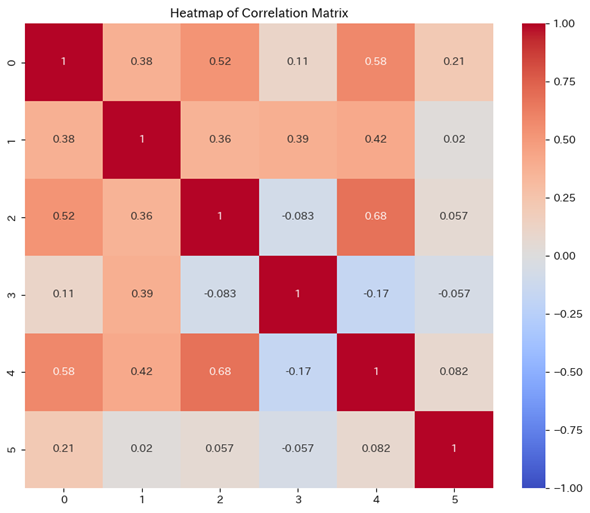
ラッソ回帰を想定して、4つの特徴量はターゲット(目的変数)に影響があり、2つが不要な特徴量となります。また、リッジ回帰を想定して、多重共線性の疑いが強まるよう特徴量間の相関(図9)は強めに設定されています。
本来であれば、さらに丁寧な前処理や、特徴量エンジニアリング、探索的データ分析などが必要ですが、本稿では、ラッソ回帰/リッジ回帰モデルの実装にフォーカスするので、そのプロセスは割愛します。
実際に使ってみよう: 機械学習モデルの訓練
次に、いよいよLasso/Ridgeクラス(sklearn.linear_modelモジュール)を使ってラッソ回帰/リッジ回帰モデルを作成し、訓練します。リスト3はそのコード例です。正則化の効果を比較するため、正則化を用いない線形回帰モデルも同時に作成しています。
from sklearn.linear_model import LinearRegression, Lasso, Ridge
# 線形回帰モデルの訓練
model = LinearRegression()
model.fit(X_train, y_train)
# ラッソ回帰モデルの訓練
lasso_model = Lasso(alpha=0.1)
lasso_model.fit(X_train, y_train)
# リッジ回帰モデルの訓練
ridge_model = Ridge(alpha=0.1)
ridge_model.fit(X_train, y_train)
# 各回帰モデルの訓練結果
print('線形回帰 の係数:', model.coef_)
print('ラッソ回帰の係数:', lasso_model.coef_)
print('リッジ回帰の係数:', ridge_model.coef_)
# 線形回帰 の係数: [0.90503157 0.00602306 0.02570293 1.38949469 0.77165554 0.51595936]
# ラッソ回帰の係数: [0.91500866 0.00436347 0. 1.26407406 0.66960111 0.41370818]
# リッジ回帰の係数: [0.90495996 0.00638464 0.02590128 1.38898153 0.7711575 0.51584978]
LassoクラスやRidgeクラスでモデル作成時に指定しているalpha=0.1は、前掲のコラムで説明したα値を表してます。ここでは初期値として0.1を指定しました。
前回も説明しましたが、係数(coefficient)はmodel.coef_属性で取得できます。訓練結果を見ると、ラッソ回帰では3つ目の特徴量の係数が完全に0.(また2つ目の0.00436347もほぼゼロ)となっており、不要な特徴量が排除される効果が分かりやすく現れています。
一方、リッジ回帰では、全体的に係数が抑制される傾向があります。例えば、1つ目の特徴量の係数は0.90503157から0.90495996へと少し小さくなっています。alpha=0.1の場合、一部の係数は小さくなっていませんが、全体として特徴量がバランス良く抑制されていることが分かります。
モデルの性能を評価してから、alpha値を調整し、再度訓練を行うことで最適なモデルを見つけるのが一般的な手順です。alpha値の調整方法については【発展】として後述します。
以上で訓練済みモデルが作成できたので、それを使って予測と評価を行ってみましょう。
実際に使ってみよう: 訓練済みモデルによる予測
リスト4は、訓練済みの各モデルを使ってテストセットからターゲットを予測するコード例です。
# テストセットを用いて予測
y_pred = model.predict(X_test) # 線形回帰
lasso_y_pred = lasso_model.predict(X_test) # ラッソ回帰
ridge_y_pred = ridge_model.predict(X_test) # リッジ回帰
# 先頭の5行を出力してみる
print(f'実際 のターゲット(先頭5行):{y_test[:5]}')
print(f'線形回帰 の予測値(先頭5行):{y_pred[:5]}')
print(f'ラッソ回帰の予測値(先頭5行):{lasso_y_pred[:5]}')
print(f'リッジ回帰の予測値(先頭5行):{ridge_y_pred[:5]}')
# 実際 のターゲット(先頭5行):[ 1.11476512 0.45862537 0.21266336 2.47469281 -2.61062525]
# 線形回帰 の予測値(先頭5行):[-0.84625175 0.41405646 -0.01181898 3.07317956 -0.99385849]
# ラッソ回帰の予測値(先頭5行):[-0.84676734 0.37430817 0.06661403 2.68987944 -0.9196915 ]
# リッジ回帰の予測値(先頭5行):[-0.84617638 0.41454519 -0.01158544 3.07259086 -0.99293168]
予測された値(=predictメソッドで取得した予測値)と実際のターゲット値(=テストセットの正解値)を比較してみると、ある程度近いものもあれば、外れているものも見受けられます。一見しただけではよく分からないので、次に「どれくらい正確に予測できているのか」を評価してみましょう。
モデルの評価と考察
リスト5は、各モデルの性能(=予測精度)を評価するコード例です。前回は決定係数(R2スコア)の他、平均二乗誤差(MSE)や平均絶対誤差(MAE)などを用いましたが、今回は話をシンプルにするため「R2スコア」のみに絞ります。
from sklearn.metrics import r2_score
# R^2スコア(決定係数)の計算
r2 = r2_score(y_test, y_pred) # 線形回帰
lasso_r2 = r2_score(y_test, lasso_y_pred) # ラッソ回帰
ridge_r2 = r2_score(y_test, ridge_y_pred) # リッジ回帰
# モデルの評価
print(f'線形回帰 のR^2スコア: {r2:.5f}')
print(f'ラッソ回帰のR^2スコア: {lasso_r2:.5f}')
print(f'リッジ回帰のR^2スコア: {ridge_r2:.5f}')
# 線形回帰 のR^2スコア: 0.78063
# ラッソ回帰のR^2スコア: 0.78298
# リッジ回帰のR^2スコア: 0.78065
リスト5を実行した結果、線形回帰のR2スコアは0.78063でした。R2スコアは1.0に近いほど良好とされるので、この結果はそこそこ良い性能を示しています。一方、ラッソ回帰ではR2スコアが0.78298に向上し、リッジ回帰も0.78065と少し改善されています。わずかながらですが、正則化の効果が確認できますね。
正則化による性能向上は、今回のように劇的でないケースも多々あります。その場合、冒頭でもコメントしましたが、決定木回帰やニューラルネットワーク回帰といった高度な手法に切り替えて、他の手法も試すことがお勧めです。引き続き、より高度な機械学習を、この連載で学んでいきましょう!
【発展】ハイパーパラメーターのチューニング(初級編)
最後に、α値などのハイパーパラメーターをチューニングする方法について説明しておきます。これは少し発展的な内容ですが、知っておくと機械学習の実践が楽になるので、ぜひ頭の片隅に入れておいてください。
前掲のリスト3では、alphaに初期値として0.1を指定しました。ですが、他の値、例えば0.01や1.0を試してみることで、さらに性能が改善するかもしれません。このような探索を手作業で行うのは非常に手間がかかるため、効率的に最適な値を見つけるためのツールを利用するのが一般的です。
具体的には、以下のツールがよく用いられます。
- GridSearchCV: scikit-learn標準搭載のクラス。候補値を指定して網羅的に検索。
- Optuna: 外部のPythonライブラリ。範囲指定で柔軟な探索が可能。
今回は、手軽に使えるGridSearchCVを使った方法を紹介します。
GridSearchCVクラスを用いる方法
リスト6は、リッジ回帰モデルを対象に、最適なα値(=Ridgeクラスでモデル作成時に指定するalphaの値)を探索するためのコード例です。0.0001、0.001、0.01、0.1、1、10という6個の候補値を指定して、これらの中で一番良い性能になるものを確定させます。
from sklearn.model_selection import GridSearchCV
# チューニングするハイパーパラメーター「α」の候補値
param_grid = {'alpha': [0.0001, 0.001, 0.01, 0.1, 1, 10]}
# GridSearchCVの動作内容を設定
grid_search = GridSearchCV(
estimator=ridge_model, # リッジ回帰モデル
param_grid=param_grid, # 候補値
scoring='r2') # R^2スコアを評価指標に指定
# 最適なハイパーパラメーター値を確定させる
grid_search.fit(X_train, y_train)
# 最適なハイパーパラメーター値を出力
print("リッジ回帰の最適なalpha値:", grid_search.best_params_['alpha'])
# リッジ回帰の最適なalpha値: 1
コード内容はコードコメントを参考にしてください。重要ポイントのみ説明します。今回は、R2スコアをモデル性能の評価指標としているためscoring='r2'と指定しています。これ以外で例えば、平均二乗誤差(MSE)を評価指標とする場合は、scoring='neg_mean_squared_error'と指定します。
ちなみに、neg_とは「負(negative)」を意味します。MSEは値が小さいほど性能が良いので、GridSearchCVではその正負を反転させることで、値が大きいほど良い指標として扱います。R2スコアは、値が大きいほど性能が良い指標なので、正負を反転させる必要がありません。
「scoringに何が指定できるか」などGridSearchCVクラスの詳細は、公式ドキュメントをご参照ください。
リスト6の結果を受けて、実際にリッジ回帰モデルの作成時にalpha=1.0を指定すると、R2スコアが0.78080となり、alpha=0.1指定時の0.78065よりもわずかに改善しました(参考:サンプルノートブック)。
今回は、ラッソ回帰とリッジ回帰の概要と仕組み、Pythonによる基本的なプログラミングを説明しました。知識を定着させるために、余裕があれば、末尾の実力試しもやってみてください。
次回は、ロジスティック回帰を取り上げます。分類問題における線形回帰の応用例を解説しますので、お楽しみに。
実力試しクイズ
オレンジ色の部分をクリックまたはタップすると答えが表示されます。ヒントが欲しい場合は、緑色の部分をクリックしてください。穴埋め問題に使える選択肢が表示されます。
問題
正則化とは、機械学習モデルの過学習(=過剰適合)を防ぐための手法であり、モデルの複雑さを抑える効果があります。
ラッソ回帰は、特徴量の係数を抑制し、一部を0(ゼロ)にすることで不要な特徴量を排除します。一方、リッジ回帰は、モデル内の全ての係数をバランス良く小さくする手法で、多重共線性を抑制する効果があります。
ラッソ回帰の正則化は、パラメーターの絶対値の合計をペナルティーとして追加します。一方、リッジ回帰ではパラメーターの二乗値の合計をペナルティーとします。
ラッソ回帰やリッジ回帰でデータセットを使用する際、特徴量間のスケールをそろえるために標準化や正規化が必要です。
scikit-learnでラッソ回帰とリッジ回帰を実装するには、それぞれLassoクラスとRidgeクラスを使用します。ハイパーパラメーターの調整には、scikit-learn標準搭載のGridSearchCVや外部ライブラリのOptunaが便利です。
ヒント: RidgeRegression 過学習(=過剰適合) SearchHyperParams 標本化 絶対値 1(ワン) LassoRegression 標準化 二乗値 GridSearchCV 極端に 多重共線性 平均値 平方根 Ridge 相関関係 Lasso 0(ゼロ) 学習不足(=過少適合) バランス良く
「機械学習入門」
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ




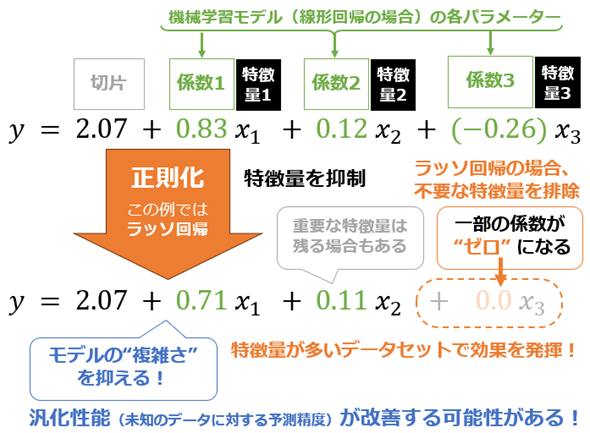

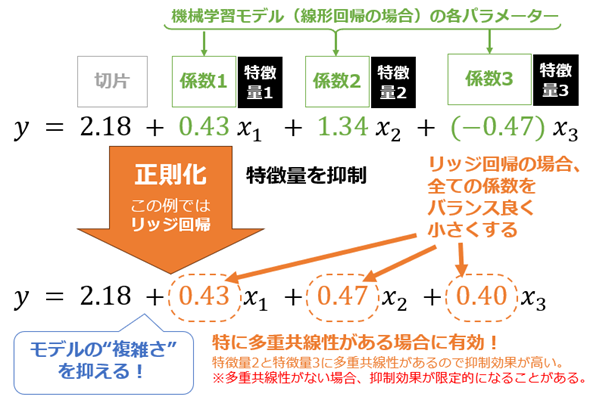

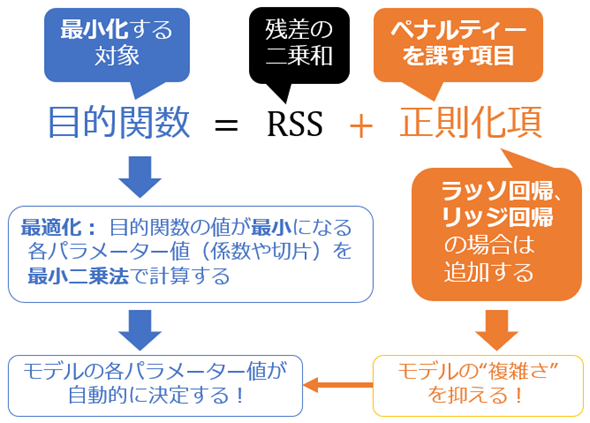
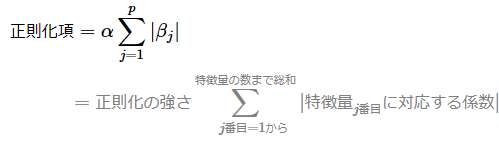
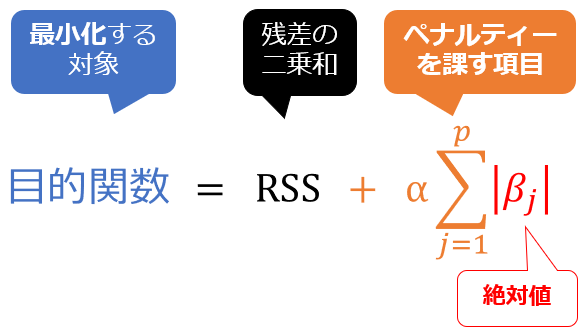 図6 仕組みの理解: ラッソ回帰の目的関数
図6 仕組みの理解: ラッソ回帰の目的関数
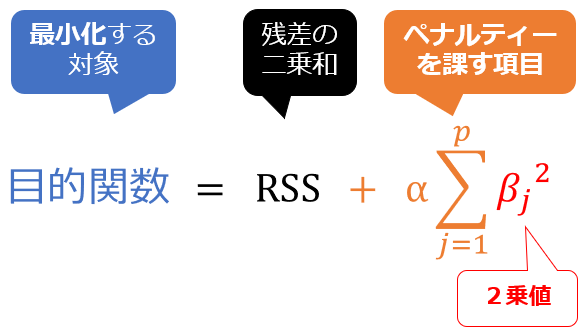 図7 仕組みの理解: リッジ回帰の目的関数
図7 仕組みの理解: リッジ回帰の目的関数