「線形回帰」(数値予測)をPythonで学ぼう:機械学習入門
「知識ゼロから学べる」をモットーにした機械学習入門連載の第3回。数値予測に使われる「線形回帰」は、最も基本的な機械学習のアルゴリズムです。その概要と仕組みを図解で学び、Pythonとscikit-learnライブラリを使った実装と実践も体験します。初心者でも安心して取り組める易しい内容です。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
ここを更新しました(公開日:2024年8月22日、更新日:2025年4月7日)
2024年12月2日最新のColab環境で、記事内の全てのコードが正常に動作することを検証しました。それに合わせて一部のコードを書き直しています。scikit-learnのバージョンは1.4以降を使う必要があります。
2025年4月7日、多項式回帰を非線形回帰の例として紹介していましたが、係数(パラメーター)に対して線形であることから、一般には線形回帰に分類されます。そのため、説明をこの観点に沿って修正しました。
販売数の予測や売上の予測など、「データの傾向を把握して、将来の予測をしたい」と思ったことはありませんか? 今回は、このような際に役立つ、機械学習の代表的な手法である線形回帰について学んでいきましょう。
具体的には、線形回帰の概要から、その仕組み、そしてPythonプログラミングによる線形回帰モデルの実装と評価まで、線形回帰の基礎スキルを短時間で習得することを目指します(図1)。線形回帰をマスターすると、ビジネスデータの分析や予測に大いに役立ちます。
第2回では、Pythonを使った機械学習プログラミングの基本的な流れを、実際にコードを書きながら体験的に学びました。よって本稿では、その内容と共通する部分はできるだけ説明を省略し、大事なエッセンスにフォーカスすることにします。
今回で学べること
線形回帰(単回帰分析や重回帰分析とも呼ばれます)は非常に有名なので、聞いたことがある人も少なくないでしょう。それぐらいに線形回帰は、データの傾向を把握して将来のデータを予測するために幅広く使われる、基本的かつ強力な手法なのです。機械学習では「最初に習得すべき必修スキル」と言えます。
図1の通り、線形回帰をプログラミングにより実現するには、第1回で紹介したPythonライブラリ「scikit-learn」が便利です。そこで本稿では、線形回帰の概念を図解で説明した後、実際にscikit-learnを使ったプログラミングを体験します。実践で役立つ基本的な使用例に絞った内容です。
もっと深く掘り下げて学びたい人は、Excelを使って学べる「やさしいデータ分析:単回帰分析」と「やさしいデータ分析:重回帰分析」や、Pythonを使って学べる「単回帰分析:手作業で計算」を併読することをお勧めします。
まとめると、今回は図2に示す内容を学ぶことができます。
それでは、まずは線形回帰の概要紹介から始めていきます。
連載:
「機械学習は難しそう」と思っていませんか? 心配は要りません。この連載では、「知識ゼロから学べる」をモットーに、機械学習の基礎と各手法を図解と簡潔な説明で分かりやすく解説します。Pythonを使った実践演習もありますので、自分の手を動かすことで実用的なスキルを身に付けられます。
本連載では、具体的な機械学習の手法(例:線形回帰、決定木、k-meansなど)を解説しています。次回以降の新着記事を見逃さないように、ぜひ以下のメール通知の登録をお願いします。
何の役に立つ手法?
線形回帰(Linear Regression)は、入力データと出力結果の関係を線形(=直線/平面/超平面、詳細は後述)でモデル化する手法です。
例えば図3は、入力データ(別名:説明変数、独立変数、特徴量)として「気温」を、出力結果(別名:目的変数、従属変数、ターゲット、ラベル)として「商品売上」を持つ架空のデータから散布図を作成し、その上に線形回帰モデルの直線(「回帰直線:regression line」とも呼ばれます)を引いた図です。
散布図の全ての点に“最も当てはまりのよい直線”(=データに“最もフィットする直線”)を引いています。これが線形回帰の本質です。この直線から、例えば気温が25℃の時は売り上げが48.81万円ということ(=予測値)が読み取れますね(図3で青色で示した部分)。
このように散布図の上に線が引ければ、例えば以下のような場面で役立ちそうです。実際に幅広い応用が可能です(冒頭の図1にも記載しています)。
- 不動産価格の予測
- 売上予測
- 生産量の予測
全て、線形で表現された回帰モデルから「何らかの数値(例:新しい不動産の価格、未来の売上、将来の生産量)を予測している」と表現できます。機械学習の線形回帰では、このようにして数値予測が行えます。
単回帰モデル
図3の直線は、中学数学で出てくる1次式のy=0.73212+1.92318xという数式で表されます(図4、各数値の取得方法は後述します)。1.92318が直線の傾きで、xは変数、ここでは「気温(℃)」で、0.73212が切片です。xにデータの「気温」を入力すると、yに計算結果の「売上(万円)」が求まります。
このように、特徴量が1つのみの線形回帰を単回帰と呼びます。まとめると単回帰(Simple Regression)は、1つの特徴量(説明変数)と1つのターゲット(目的変数)の関係を「直線」でモデル化する手法です。
線形回帰の傾きや切片は、変数に「係(かか)る数(=かけ算する数)」であるため、回帰係数(かいきけいすう:regression coefficient)とも呼ばれます。切片(intercept)も1に対する係数と考えることができます。係数の大きさが、係る変数の影響の大きさを表します。
重回帰モデル
しかし、特徴量が1つしかないケースはあまりないでしょう。例えば賃貸物件の価格であれば、部屋数や築年数、駅からの距離など、さまざまな条件があります。多数の条件を特徴量として入力するはずです。
このように、特徴量が複数ある線形回帰を重回帰(Multiple Regression)と呼びます。重回帰は、複数の特徴量と1つのターゲットの関係を「平面」や「超平面」でモデル化する手法です。
例えば特徴量が2つあると、図5のように3次元座標空間にプロットした散布図に平面(回帰平面:regression plane)を描くことになります。
図5の平面も、直線と同じく1次式でy=1.40805+4.62026x1+0.00536x2という数式で表されます。4.62026が変数x1(=部屋数)に対する係数(平面の傾き)で、0.00536が変数x2(=築年数)に対する係数(平面の傾き)、1.40805が切片です。x1とx2にデータの「部屋数」と「築年数」を入力すると、yに計算結果の「賃貸価格(万円)」が求まります。
ちなみに、特徴量に「駅からの距離(km)」を含めたい場合は、「逆数」、つまり1/距離(=距離分の1)という形で表現することをお勧めします。これにより、距離が近いほど賃貸価格に大きな影響を与えるようになります。
なお、特徴量が3つ以上ある場合、線形回帰モデルは直線や平面ではなく、より高次元の空間での超平面(回帰超平面:regression hyperplane)になります。ただし、4次元以上の空間にプロットすることになるため、図5のようなグラフを描くのは難しくなります。
【コラム】回帰分析とは
ここまで「線形回帰」という用語で説明してきましたが、似た用語に「回帰分析」があります。一般的に「回帰分析」と言えば、「線形回帰」が想定されることが多いですが、実際には以下のように多くの手法が含まれます(今回は名前だけ紹介します。多数あることを確認してください)。
- 線形回帰
- リッジ回帰
- ラッソ回帰
- 多項式回帰
- サポートベクター回帰
- 決定木回帰
- ランダムフォレスト回帰
- 勾配ブースティング回帰
- ニューラルネットワーク回帰
このように、広義の回帰分析(Regression Analysis)は、特徴量(説明変数)とターゲット(目的変数)の関係をモデル化し、主に「数値を予測する」(=回帰の)ために使われます。
一般的に、「回帰分析」と表現する場合、統計学的な分析を重視することが多いです。例えば、先ほどの重回帰モデルでは、「部屋数」にかけ算する係数が4.18873でした。この数値から、「賃貸価格」に対する「部屋数」の影響度が説明できます。統計学ではこのような説明や分析が重要です。一方で、機械学習では予測を重視することが多いです。
【コラム】線形回帰と非線形回帰の違い
「線形」な回帰があるからには、当然「非線形」な回帰も存在します。非線形回帰(Nonlinear Regression)は、線形モデルでは表現できない「複雑な特徴量(説明変数)とターゲット(目的変数)の関係」をモデル化するために使用されます。
例えば以下のような手法が非線形回帰に含まれます。
これらの回帰モデルでは、本稿で紹介したような一次式に加え、ax(aのx乗)のような指数関数型の式など、非線形な数式が用いられます。非線形回帰は、例えば「生物の成長曲線」など、直線では表現できない非線形な特性を扱う際に、“当てはまりのよいモデル”にするために有用です。
ちなみに、多項式回帰(参考記事)は、x2(xの2乗)のような非線形な特徴量(入力変数)を使って曲線をモデル化しますが、各パラメーター(係数)が線形(=定数倍など直線的)であるため、一般には線形回帰の一種と見なされます。
【注意】モデルが適用できる範囲
線形回帰モデルは、機械学習モデルの訓練に使う入力データ(特徴量)の範囲内でのみ正確な予測ができます。これを内挿(ないそう、Interpolation)と呼びます。
一方、その範囲外の入力データ、つまり今まで訓練に使用したことがない範囲のデータによる予測は、外挿(がいそう、Extrapolation)と呼ばれます(図6)。
図6では、背景がピンク色のエリアが外挿となります。このエリアでの予測は、信頼性が低いことに注意が必要です。モデルが学習していないエリアでは、実際の関係性が大きく異なる可能性があるためです。
従って、外挿の範囲での予測は避けることが推奨されます。可能であれば、範囲外のデータを新たに取得して訓練をし直しましょう。
以上で「線形回帰がどのようなものか」が分かったと思います。先ほどの単回帰モデルとしてはy=0.73212+1.92318xといった数式を示しましたが、0.73212という切片や1.92318という係数は、機械学習の訓練によって自動的に決定(=最適化)されます。その仕組みを次に説明します。
どんな仕組み?
係数となるパラメーター(parameters)は、数学的な計算によって決まります。線形回帰では、一般的に最小二乗法(Ordinary Least Squares:OLS)と呼ばれる計算方法が使われます。以下で、その仕組みをできるだけ数式ではなく図解を中心に説明していきます。
ステップ1: 訓練セットを準備
データに最も当てはまりのよい線形回帰モデル(回帰直線/平面/超平面)の各パラメーターを見つけるためには、まずは訓練用のデータセットを準備する必要があります。以下の説明では、先ほどの単回帰モデルと同じデータを使うとしましょう(図7)。このデータには、特徴量(x)として「気温」が、ターゲット(y)として「売上」があります。
ステップ2: 仮の回帰直線を設定
切片をパラメーターβ0、気温(x)に対する係数(直線の傾き)をパラメーターβ1と置くと、数式は以下のようになります。
今回は図解で説明するために、各パラメーターに対する仮の初期値を設定します。この初期値はあくまで「仮」なので、好きに決めて構いません。ここではβ0の初期値は30.0、β1の初期値を0.5としましょう。
これにより、y=30.0+0.5xという数式の回帰直線になります。図8に、この直線を描いてみました。
デタラメな初期値だったので、データと直線がフィットしていませんね。これを最適な直線(=データに“最も当てはまりのよい直線”)に調整します。
ステップ3: 残差を計算
ここで「仮の回帰直線が、実際のデータからどれくらいズレているか」を計算します。
この場合のズレとは、「各データポイント」と「仮の回帰直線(=線形回帰モデル)」の間の距離です。具体的には、各データポイントのターゲット(ここでは「売上」)から、回帰直線の出力値(=線形回帰モデルによる予測値)を引くことで、距離が計算できます。この計算方法による距離は、厳密には残差(residuals)と呼ばれます。
図9は、残差を視覚化した例です。y軸の売上に対するズレを計測しているので、縦に垂直な距離計算となります。
しかし、この残差には+(プラス)や−(マイナス)があるので、全ての残差を足し合わせていくと、例えば+2と−2で打ち消されてしまい、ズレがないことになってしまう問題があります。そうならないよう、「残差の2乗値(=残差×残差の値)」を求めることで全ての残差を+(プラス)にします。
ステップ4: 残差の二乗和(RSS)の計算
そして、「残差の2乗値」を全て足し合わせることで、全てのデータに対するズレ(を2乗した値)の合計値が算出できます。このズレの合計値が最も小さくなるような切片と傾きが見つかれば、それが「データに“最も当てはまりのよい直線”が得られた」ということです。
このズレの合計値は、統計学寄りの回帰分析では残差平方和(RSS:Residual Sum of Squares)と呼ばれ、機械学習寄りの線形回帰では他の機械学習モデルの用語に合わせて二乗和誤差(SSE:Sum of Squared Error)と呼ばれることが多いです。本稿では、伝統的な統計学の用語に従って残差の二乗和(略語はRSS)と表記することにします。
「残差」と「誤差」という用語には違いがあります。少し混乱しやすい概念なので、とにかく「違いがある」ということを知っておくだけでも構いません。
特に統計学では、誤差は「観測値(=目的変数/ラベルの値)」と「真の値」の差を指します。ただし通常、この「真の値」は分かりません。一方、残差は「観測値」と「(モデルによる)予測値」の差です。つまり、残差は実際のデータとモデルのズレを示すため、統計学寄りでは「誤差」よりも「残差」という用語が適切です。
対して、ニューラルネットワークなどの機械学習では、二乗和誤差(SSE)という表記がよく使われます。この場合の誤差は、「(モデルによる)予測値」と「正解値(=教師データとなる観測値/目的変数/ラベル)」の差を指します。機械学習では、「正解値」が「真の値」と仮定されるので、予測値と真の値の差を「誤差」と呼びます。
まとめると残差の二乗和(RSS)の数式は、以下のようになります。
観測値i番目−予測値i番目が残差です。残差の計算は、逆順で予測値i番目−観測値i番目としても構いません(2乗するので、計算結果は同じです)。
残差を図解するためにステップ2で仮のパラメーター初期値を設定しましたが、この初期値をなくして、予測値i番目の部分を元の回帰直線の数式に戻しましょう。以下のようになります。
この数式から、数学計算により最適なパラメーターを求めます。数学計算の内容は、本稿では割愛するので、詳しく学びたい方は記事「機械学習の数学:回帰分析」を参照してください。
本稿では、パラメーターβ0(切片)やパラメーターβ1(気温に対する係数)を求める方法を、より直感的な図を使って解説します。なお、データに最適なモデルのパラメーターを求めることをパラメーター推定(parameter estimation)と呼びます。最小二乗法はその一例です。
一般的な最小二乗法の数学計算は、少し難しい用語になりますが、偏微分して傾きが0になるように計算する「解析的に解く方法」です。それに対し、以下で説明する内容は、さまざまなパラメーター値を試して最適な値を見つける「数値的に解く方法」となります。
ステップ5: 残差の二乗和(RSS)の最小化
数値的に解く方法は、分かりやすく言うと「手当たり次第に試す方法」です。数学の公式を使わないので直感的に理解できるメリットがありますが、ムダが多くて時間がかかるデメリットもあります。ここではパラメーターβ0とβ1に、手当たり次第に値を入れてみましょう。
具体的には、β0(切片)に-100〜100の範囲で0.01刻みに数値(=合計20000個)を入れ、β1(係数)に0〜4の範囲で0.01刻みに数値(=合計400個)を入れます。2つのパラメーターの組み合わせ数は20000×400=800万と大量なので、RSS(残差の二乗和)の計算処理に時間がかかりますね。
大量の組み合わせの中で、RSSの計算値が最も小さいものが「最適なパラメーター」です(=RSSの最小化)。ここでの最適なパラメーターは、β0(切片)が0.8、ーβ1(気温に対する係数)が1.92と求まりました(詳細はサンプルノートブックを参照してください)。
上記の計算結果を図で視覚的に確認してみましょう。「RSSの計算結果が、どのように最適なパラメーターを導き出しているのか」が目で見て理解できるようになります。なお、2つのパラメーターを同時に図示すると3次元グラフになりますが(参考:サンプルノートブック)、ここではβ0とβ1を個別に2次元グラフでより分かりやすく図解します。
まずはβ0が決定する部分を可視化します。図10は、線形回帰モデルのパラメーターβ1(気温に対する係数)を先ほど得られた1.92で固定して、パラメーターβ0(切片)にさまざまな値を入力してみた場合の、RSS(残差の二乗和)の値をグラフ化したものです。
このグラフを見ると、RSSの値が一番小さいのは曲線の最下部にあるオレンジ色の点ですね。このグラフから、β0は0.8と求まりました。
次にβ1が決定する部分を可視化します。図11は、線形回帰モデルのパラメーターβ0(切片)を先ほど得られた0.8で固定して、パラメーターβ1(気温に対する係数)にさまざまな値を入力してみた場合の、RSS(残差の二乗和)の値をグラフ化したものです。
このグラフを見ると、RSSの値が一番小さいのは曲線の最下部にあるオレンジ色の点なので、β1は1.92と求まりました。
数値的に解く方法では、このようにして各パラメーターを見つけられます。線形回帰で一番難しい部分ですが、図解でできるだけ分かりやすく説明してみました。
なお、scikit-learnなどの内部では、最適なパラメーターの値が解析的に計算されます。数学の公式を使うので計算精度が高く、しかも高速です。
ステップ6: 最適な回帰直線の決定
以上で、RSSが最小となる最適なパラメーターβ0とβ1が計算できたので、これらを用いて最終的な線形回帰モデル(ここでは回帰直線)を決定します。数式は以下のようになります。
この数式の回帰直線を散布図上に描画すると図12のようになります。
以上のように最小二乗法は、訓練セットに最も適した線形回帰モデル(回帰直線/平面/超平面)を見つけるための計算方法というわけです。
ちなみに、数値的に解く方法は、探索範囲や刻み幅によって解の精度が左右されることがあり、数学計算により解析的に解く方法よりも精度が低くなる可能性があります。実際に、ここで説明した最小二乗法の計算を解析的に解くと、以下のようになります(図13、参考:サンプルノートブック)。切片β0の値が少し異なる結果となりました。
- 解析的な方法で求めたβ0: 0.73(数値的な方法では0.8)
- 解析的な方法で求めたβ1: 1.92(数値的な方法でも1.92)
- 回帰直線の方程式: y=0.73+1.92x(数値的な方法ではy=0.8+1.92x)
以上で、線形回帰モデルの各パラメーターがどのように決定されるかの仕組みを理解しました。続いて実践として、scikit-learnを使ってプログラムを作成してみましょう。
仕組みの説明では、図解による分かりやすさを重視して単回帰の例を用いましたが、ここからは、より実践的な複数の特徴量を使った重回帰を試してみましょう。特徴量を1つにするだけで、簡単に単回帰に切り替えられるので、単回帰も同時にマスターできます!
体験してみよう
scikit-learnには、単回帰/重回帰モデルを構築できるLinearRegressionクラス(sklearn.linear_modelモジュール)があります。
LinearRegressionクラスの使い方
LinearRegressionクラスをインスタンス化(例:modelオブジェクトを作成)したら、訓練セットで訓練をするfit()メソッドを呼び出すだけです(リスト1)。訓練された線形回帰モデルを使って予測(predict)するには、predict()メソッドを使います。
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(<特徴量:X>, <ターゲット:y>)
model.predict(<新しいデータ>)
scikit-learnでの機械学習は、基本的にこのパターンで使います。「fit」は、「適合(フィット)する」という意味で、訓練セットに適合する(=訓練する)ことです。
もちろんLinearRegressionクラスには、これ以外の機能も備わっています。詳しくは公式ページを参照してください(※英語ですので、日本語で読みたい場合は、Webブラウザ「Google Chrome」の[日本語に翻訳]機能などを使ってください)。
それでは、このクラスを使って、実際に線形回帰モデルを作成し、重回帰を行ってみましょう。
ノートブックの利用について
本連載は、第1回で説明したように、無料のクラウド環境「Google Colab」の利用を前提としています。基本的には、Colabで新規ノートブックを作って、以降で説明するコードを入力しながら実行結果を自分の目で確かめてください。既に入力済みのノートブックを使いたい場合は、こちらのサンプルノートブックをご利用ください。
実際に使ってみよう: データセットの読み込み
まずはデータセットを準備する必要があります。今回はscikit-learnから読み込める「California Housing(カリフォルニア住宅価格)データセット」を使います。入力データとなる特徴量には、下記の8項目があります。
- MedInc(median income): 所得(中央値)
- HouseAge(median house age): 築年数(中央値)
- AveRooms(avarage number of rooms): 部屋数(平均値)
- AveBedrms(avarage number of bedrooms): 寝室数(平均値)
- Population: 人口
- AveOccup(average occupancy rate): 世帯人数(平均値)
- Latitude: 緯度
- Longitude: 経度
出力結果となるターゲットは以下の通りです。
- MedHouseVal(median house value): 住宅価格(中央値)
線形回帰の説明では、身近な例として理解しやすい「住宅価格」のデータセットがよく用いられます。California Housingデータセットは、機械学習の初心者が初めて扱うデータとして最適です。
線形回帰に向いていないデータもあります。例えば時系列で、単純な線形関係で捉えられない複雑な動きをする株価データなどです。他のデータセットを試す際にはご注意ください。
California Housingデータセットについてより詳しく知りたい場合は、こちらの記事を参照してください。
このデータセットを読み込むには、sklearn.datasets.fetch_california_housing()関数を呼び出すだけです。訓練セットとテストセットに分割するまでのコードを以下のリスト2に示します。
from sklearn.datasets import fetch_california_housing
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
# データセットの読み込み
housing = fetch_california_housing()
# 特徴量とターゲットの取得
X = housing.data
y = housing.target
# データの標準化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 訓練セットとテストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.1, random_state=0)
print(f'訓練セットのサイズ: {X_train.shape}') # 訓練セットのサイズ: (18576, 8)
print(f'テストセットのサイズ: {X_test.shape}') # テストセットのサイズ: (2064, 8)
リスト2では、前処理としてデータを標準化(参考:前回のコラム)しています。標準化は、各特徴量で平均を「0」に、標準偏差を「1」のスケールに変換する手法です。
本来であれば、データを分割する前にデータ内容をよく調べて、丁寧な前処理や、特徴量エンジニアリング、探索的データ分析をする必要があります。詳しくは第2回の記事を参照してください。California Housingデータセットの前処理については、『Pythonデータ処理入門:NumPy超入門』の第9回〜第12回をご一読ください。本稿では、線形回帰の実装にフォーカスするので割愛します。
実際に使ってみよう: 機械学習モデルの訓練
次に、いよいよLinearRegressionクラス(sklearn.linear_modelモジュール)を使って線形回帰モデルを作成し、訓練します。リスト3はそのコード例です。
from sklearn.linear_model import LinearRegression
# 線形回帰モデルの訓練
model = LinearRegression()
model.fit(X_train, y_train)
print('係数:', model.coef_)
print('切片:', model.intercept_)
# 係数: [ 0.82585077 0.1184866 -0.25575322 0.29521609 -0.00616386 -0.05498614
# -0.89616681 -0.86657695]
# 切片: 2.0683578901986106
線形回帰の概要や仕組みを理解するのにはやや骨が折れますが、scikit-learnで機械学習モデルを作るのは拍子抜けするぐらいに簡単ですね。
リスト3に示したように、係数(coefficient)はmodel.coef_属性で、切片(intercept)はmodel.intercept_属性で取得できます。これらを使えば、「図3 線形回帰モデルの回帰直線の例」のようなグラフも作成できますね(※この例ではパラメーター数が多いため、高次元の空間となりグラフにできません)。
実際に使ってみよう: 訓練済みモデルによる予測
次に、リスト4はそのモデルを使ってテストセットから住宅価格を予測するコード例です。リスト3とリスト4は、最初に示したリスト1とほぼ同じですね。
# テストセットを用いて予測
y_pred = model.predict(X_test)
# 先頭の5行を出力してみる
print(f'予測の住宅価格(先頭5行):{y_pred[:5]}')
print(f'実際の住宅価格(先頭5行):{y_test[:5]}')
# 予測の住宅価格(先頭5行): [2.27471227 2.78176818 1.89960405 1.0228928 2.94939876]
# 実際の住宅価格(先頭5行): [1.36900000 2.41300000 2.00700000 0.7250000 4.60000000]
※比較しやすいように「実際の住宅価格」の出力例には「0」を書き足して桁をそろえました。
予測された住宅価格(=predictメソッドで取得した予測値)と、実際の住宅価格(=テストセットの正解値)は、パッと見で近いような、外れているような感じがしますね。よく分からないので、どれくらい正確に予測できているかを評価してみましょう。
モデルの評価と考察
リスト5が、線形回帰のモデルを性能(=予測精度)を評価するコード例です。
from sklearn.metrics import r2_score, mean_squared_error, root_mean_squared_error, mean_absolute_error
# R^2スコア(決定係数)の計算
r2 = r2_score(y_test, y_pred)
# MSE(平均二乗誤差)の計算
mse = mean_squared_error(y_test, y_pred)
# RMSE(平均二乗誤差の平方根)の計算
rmse = root_mean_squared_error(y_test, y_pred)
# MAE(平均絶対誤差)の計算
mae = mean_absolute_error(y_test, y_pred)
# モデルの評価
print(f'決定係数(R^2スコア): {r2:.2f}') # 決定係数(R^2スコア): 0.61
print(f'平均二乗誤差(MSE): {mse:.2f}') # 平均二乗誤差(MSE): 0.54
print(f'平均二乗誤差の平方根(RMSE): {rmse:.2f}') # 平均二乗誤差の平方根(RMSE): 0.73
print(f'平均絶対誤差(MAE): {mae:.2f}') # 平均絶対誤差(MAE): 0.53
リスト5では、さまざまな評価指標で評価しています。以下に箇条書きで、それぞれの評価指標についてまとめます。計算方法や数式については省略するので、各項目のリンク先を参照してください。
- 決定係数(R2スコア):
- 線形回帰モデルによる予測が「観測データ(正解データ)にどれくらい当てはまるか」の割合を示す評価指標。
- 評価値: 範囲は通常、0(=0%)〜1.0(=100%、※マイナスになることもある)で、値が大きい(=1.0に近い)ほど良好。
- コード: sklearn.metricsモジュールのr2_score関数で計算できる。
- 注意点: 特徴量(説明変数)の数が増えるほど1.0に近づく性質があり、過剰適合(=過学習:Over-fitting)や過少適合(=学習不足:Under-fitting)を見逃す可能性がある。そのため、モデルの複雑さを考慮した自由度調整済み決定係数(Adjusted R2)を使うこともある。
- 平均二乗誤差(MSE:Mean Squared Error):
- 予測値と正解値(=実際の観測値)の誤差の大きさを示す評価指標。誤差を2乗するため、誤差の単位が大きくなる。
- 評価値: 範囲は0以上で、値が小さい(=0に近い)ほど良好。
- コード: sklearn.metricsモジュールのmean_squared_error関数で計算できる。
- 注意点: 誤差の2乗を取るため、異常値(外れ値)の影響を受けやすい。外れ値が多い場合には、他の指標と併用することが望ましい。
- 平均二乗誤差の平方根(RMSE:Root Mean Squared Error):
- 予測値と正解値(=実際の観測値)の誤差の大きさを示す評価指標。2乗した誤差の平方根を取ることで、元のデータと同じ単位に戻す。同じ単位で評価できるため、解釈がしやすい。
- 評価値: 範囲は0以上で、値が小さい(=0に近い)ほど良好。
- コード: sklearn.metricsモジュールのmean_squared_error関数で引数にsquared=Falseを指定することで、scikit-learnのバージョンが1.4以降の場合はsklearn.metricsモジュールのroot_mean_squared_error関数で計算できる。
- 注意点: MSEと同じく異常値(外れ値)の影響を受けやすいので、他の指標との併用が望ましい。
- 平均絶対誤差(MAE:Mean Absolute Error):
- 予測値と正解値(=実際の観測値)の誤差の大きさを示す評価指標。誤差の絶対値を取るため、データと同じ単位のままになる。同じ単位で評価できるため、解釈もしやすい。
- 評価値: 範囲は0以上で、値が小さい(=0に近い)ほど良好。
- コード: sklearn.metricsモジュールのmean_absolute_error関数で計算できる。
- 注意点: MSEやRMSEよりも異常値(外れ値)の影響を受けにくい利点があるが、その分、誤差が大きくても過大には評価されないため、評価が難しくなることもある。
これらの複数の評価指標を使うことで、特定の評価指標による偏りや不正確な評価を避けることができます。例えば、R2スコアが高くても、RMSEやMAEが大きい場合、「モデルの性能に問題(例えば過剰適合や外れ値の影響など)があるかもしれない」と判断できるようになります。
どの評価指標を使うかはケース・バイ・ケースで、他の指標(例えばMAPE《平均絶対パーセント誤差》やMSLE《平均二乗対数誤差》など)を使うこともあります。一般的には、R2スコア(決定係数)とRMSE(平均二乗誤差の平方根)の2つを併用するのがお勧めです。以下に「評価指標の使い分け指針」をまとめます。
- モデルの全体的な性能を評価したい場合: R2が適している。
- モデルの複雑さを考慮して性能を評価したい場合: Adjusted R2が適している。特徴量の数が増えるとペナルティーが加わり、過剰適合を避けられる。
- モデルの訓練方法(最小二乗法)と同じように評価したい場合: MSEが適している。RSS(残差の二乗和)をデータ数で割って平均すると、MSEと同じ計算式になるから。
- 解釈性を重視する場合: RMSEが適している。
- 異常値(外れ値)の影響を避けたい場合: MAEが適している。
前置きが長くなりましたが、リスト5を実行した結果、R2スコアは0.61(=モデルがデータの約61%に当てはまる)となりました。1.0に近い方が良好なので、一般的なケースで見ると、このモデルの性能はそれほど良くありませんね。また、RMSEは0.73となり、0.0に近い方が良好なので、こちらの評価指標でも性能はそれほど良くありません。このモデルには改良の余地がありそうです。
実際に筆者が他の機械学習手法、具体的にはランダムフォレスト回帰(今後解説予定)を試したところ、R2スコアは0.59から0.81に、RMSEは0.73から0.51に大きく改善されました。リスト3のLinearRegressionクラス(sklearn.linear_modelモジュール)をRandomForestRegressorクラス(sklearn.ensembleモジュール)に書き換えると試せます(詳しくはサンプルノートブックを参照してください)。
線形回帰は機械学習の基本ですが、その性能向上には限界があります。よって、より高度な機械学習を、この連載で引き続き学んでいきましょう!
【発展】知っておくべき多重共線性の検出方法
最後に、線形回帰に特有の問題について説明しておきます。これは少し発展的な内容ですが、線形回帰を実践するなら、ぜひ頭の片隅に入れておいてください。
多重共線性(Multicollinearity)は、特徴量(説明変数)同士が強い相関を持つことを指します。この問題があると、モデルのパラメーター推定が不安定になり、結果として予測精度(=モデルの性能)が低下する可能性があります。
今回は、初めて線形回帰をプログラミングする人に向けて、仕組みの理解と最もシンプルなコーディングを重要視して説明してきました。しかし、より実践的には、モデルを作り始める前にデータセットに深く向き合い、「多重共線性がないかどうか」も確かめておくべきです。
多重共線性を検出するには、以下の方法が取れます。
- 相関行列を用いる方法: 各特徴量間の相関係数を計算する。高い相関がある特徴量間には多重共線性が疑われる。
- 分散膨張係数(VIF:Variance Inflation Factor)を用いる方法: VIFが高い(一般的には10を超える)特徴量は、多重共線性が疑われる。
それでは、先ほどと同じCalifornia Housingデータセットを使って、多重共線性が存在するかどうかを確認してみましょう。
相関行列を用いる方法
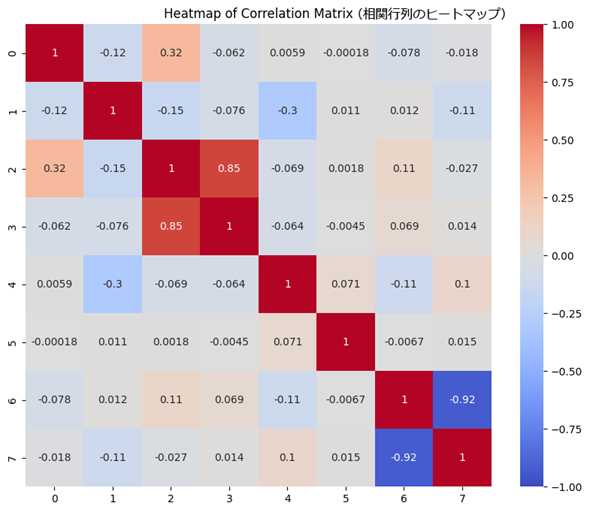
リスト6は、データセットの各特徴量同士の相関行列を計算し、そのヒートマップ図を表示するコード例です。図14が、その図です。
# リスト2のコードの後に以下を記述する
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# 訓練セットをpandas DataFrame化
X = pd.DataFrame(X_train)
# 相関行列の計算
corr_matrix = X.corr()
# 相関行列のヒートマップ図の表示
plt.figure(figsize=(10, 8))
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm', vmin=-1, vmax=1)
plt.title('Heatmap of Correlation Matrix')
plt.show()
seabornモジュールのheatmap関数を使っています。コード内容の説明は割愛しますので、コードコメントを参考にしてください。
図14より、AveRooms(部屋数)とAveBedrms(寝室数)の相関係数が0.85とプラス方向に強いことが分かります。これは「強い正の相関」を示しています(相関係数の見方は、こちらの用語解説を参考にしてください)。
つまり、「これらの特徴量の両方を使うと、多重共線性が発生する可能性がある」ということです。従って、AveRoomsだけを使うなどの対策が一般的に推奨されます。
また、Latitude(緯度)とLongitude(経度)の相関係数が-0.92とマイナス方向に強いことが分かります。これは「強い負の相関」を示しています。よって、どちらか一方を採用するか、あるいは両方とも特徴量から外すことを検討するのが一般的です。
しかし、今回はAveBedrms、Latitude、Longitudeの3つの特徴量を外しても、(筆者が試した限りでは)モデルの性能は向上しませんでした。このように多重共線性への対処は必ずしも性能改善につながるわけではありませんが、「モデルの解釈のしやすさ」という観点では重要です。また今回の例では、欠損値などの前処理をしていないなど多重共線性以外の要因や、除去した特徴量に重要な情報が含まれていた可能性が考えられます。特徴量選択の際には、他の手法(例えば次回解説するリッジ回帰やラッソ回帰)も併用するとよりよいでしょう。
分散膨張係数(VIF)を用いる方法
次に、各特徴量のVIFを計算して表示します(リスト7)。
# リスト2のコードの後に以下を記述する
import pandas as pd
from statsmodels.stats.outliers_influence import variance_inflation_factor
# 訓練セットをpandas DataFrame化
X = pd.DataFrame(X_train)
# VIFの計算
vif_data = pd.DataFrame()
vif_data['Feature'] = housing.feature_names
vif_data['VIF'] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
# VIFの結果を評価
print(vif_data)
# Feature VIF
# 0 MedInc 2.506234
# 1 HouseAge 1.247925
# 2 AveRooms 8.468261
# 3 AveBedrms 7.117997
# 4 Population 1.141382
# 5 AveOccup 1.007791
# 6 Latitude 9.325308
# 7 Longitude 8.999270
統計モデルに関する機能を提供するPythonライブラリ「statsmodels」にあるstatsmodels.stats.outliers_influenceモジュールのvariance_inflation_factor関数を使っています。コード内容の詳細説明は割愛しますので、コードコメントを参考にしてください。
VIF(分散膨張係数)は、多重共線性の程度を測る指標で、「各特徴量が他の特徴量とどのくらい相関しているか」を示します。一般的には以下の基準で判断するとよいでしょう。
- VIF = 1: 各特徴間に相関がない。
- 1 < VIF ≤ 10: 各特徴間に中程度の相関があるが、許容範囲内。
- 一般的には1 < VIF ≤ 5が望ましい。
- VIF > 10: 各特徴間に高い相関があり、多重共線性が疑われる。
リスト7の出力結果を見ると、AveRooms、AveBedrms、Latitude、Longitudeという4つの特徴量は、VIFの値が高めです(※データを標準化しない場合には、これらのVIFは10を超えました)。つまり、これらは多重共線性の問題を引き起こす可能性があります。
特にLatitudeとLongitudeのVIFはそれぞれ9.3と8.9と高く、これらの特徴量には多重共線性が疑われます。また、AveRoomsとAveBedrmsのVIFもそれぞれ8.4と7.1とやや高く、これらの特徴量にも多重共線性が疑われます。これらの結果は、前掲(図14)の相関行列のヒートマップ図とほぼ同じですね。
このVIFの計算結果を基に「多重共線性が存在する特徴量」を検出し、必要に応じて適切な対策を講じることで、モデルの性能を向上させられる可能性があります。今回は、多重共線性が疑われる特徴量を除外しても、(筆者が試した限りでは)モデルの性能は向上しませんでしたが、これは前述の相関行列の結果と同様です。
今回は、Pythonによる線形回帰の概要と仕組み、基本的なプログラミングを説明しました。知識を定着させるために、余裕があれば、末尾の実力試しもやってみてください。
次回は、線形回帰の続編としてリッジ回帰やラッソ回帰を解説します。お楽しみに。
実力試しクイズ
オレンジ色の部分をクリックまたはタップすると答えが表示されます。ヒントが欲しい場合は、緑色の部分をクリックしてください。穴埋め問題に使える選択肢が表示されます。
問題
線形回帰は、入力データ(特徴量、説明変数)と出力結果(ターゲット、目的変数)の関係を線形(=直線/平面/超平面)でモデル化する手法です。scikit-learnでは、線形回帰はLinearRegressionクラスを使って実装できます。
線形回帰のうち、単回帰は1つの特徴量と1つのターゲットの関係をモデル化し、重回帰は複数の特徴量と1つのターゲットの関係をモデル化します。
単回帰モデルを表す回帰直線の数式は、回帰係数と切片を用いて表現されます。これらのパラメーターは、データセットに最も適した直線を引くために最小二乗法により計算されます。
線形回帰モデルの性能を評価するためには、決定係数(R2スコア)やRMSE(平均二乗誤差の平方根)などの評価指標が使われます。
多重共線性は、特徴量同士が強い相関を持つ場合に発生する問題です。これを検出するためには、相関行列やVIF(分散膨張係数)を用いる方法があります。
ヒント: 相関行列 R2 係数 LinearModel 傾き 多項式回帰 VIF 関係 LinearRegression 平均二乗誤差 K2 RMSE 重回帰 相関 VIP 切片 MAPE 共分散行列 最小二乗法 定数
「機械学習入門」
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ

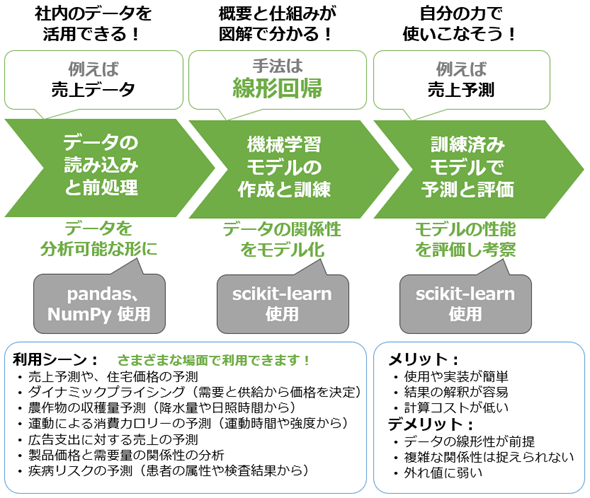


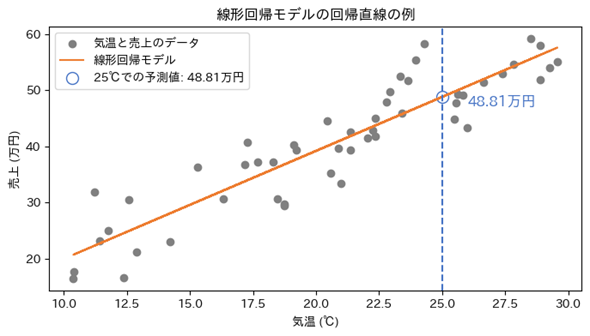
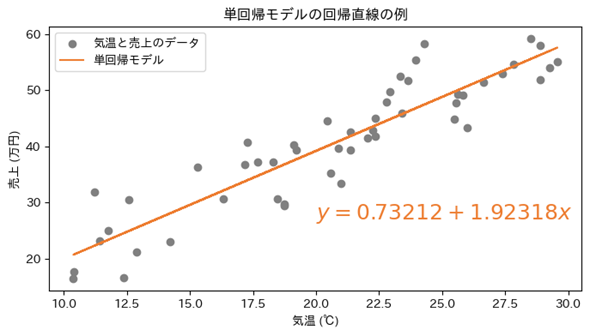

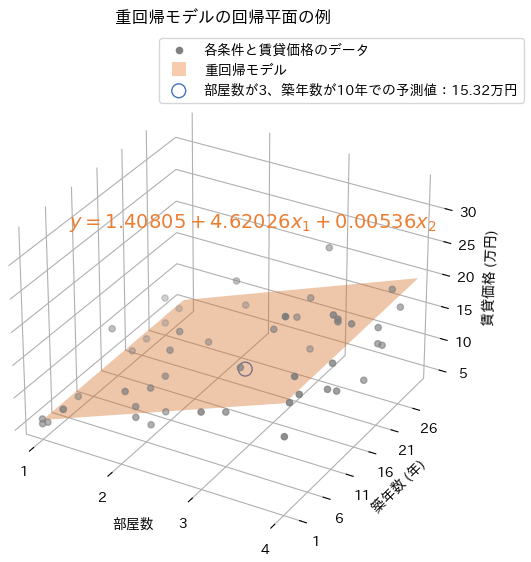 図5 重回帰モデルでの回帰平面の数式
図5 重回帰モデルでの回帰平面の数式
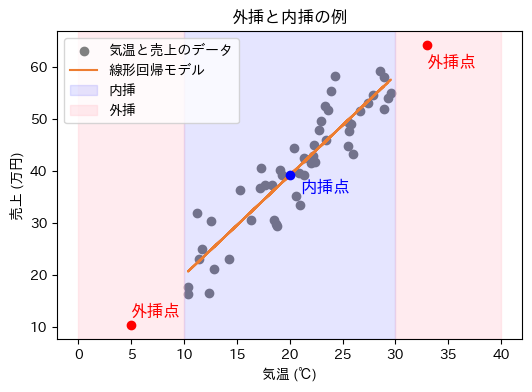 図6 回帰モデルでの内挿と外挿
図6 回帰モデルでの内挿と外挿
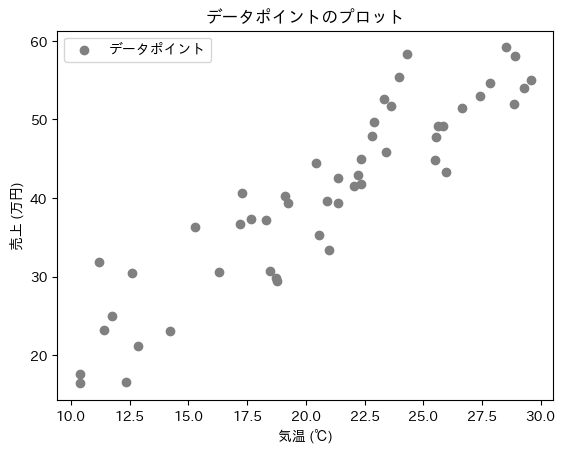 図7 仕組みの理解: 訓練セットをプロットした散布図
図7 仕組みの理解: 訓練セットをプロットした散布図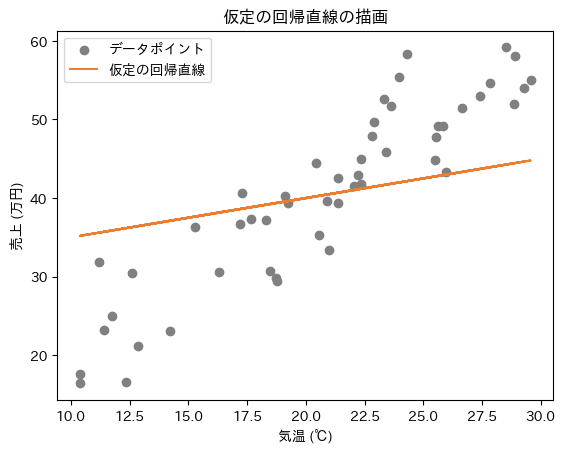 図8 仕組みの理解: 散布図上に描画した仮定の回帰直線
図8 仕組みの理解: 散布図上に描画した仮定の回帰直線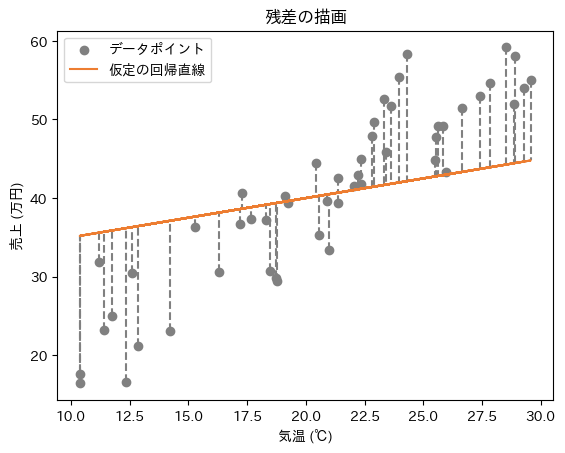 図9 仕組みの理解: 各テータポイントと仮の回帰直線の残差
図9 仕組みの理解: 各テータポイントと仮の回帰直線の残差


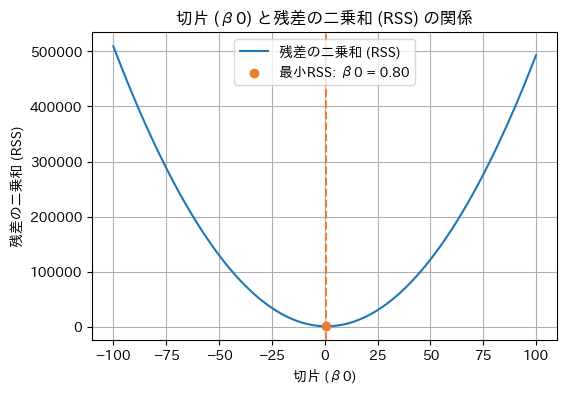 図10 仕組みの理解: RSSが最小化する「切片」の値
図10 仕組みの理解: RSSが最小化する「切片」の値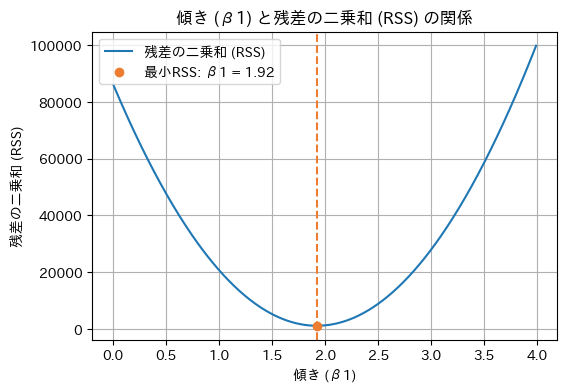 図11 仕組みの理解: RSSが最小化する「気温に対する係数」の値
図11 仕組みの理解: RSSが最小化する「気温に対する係数」の値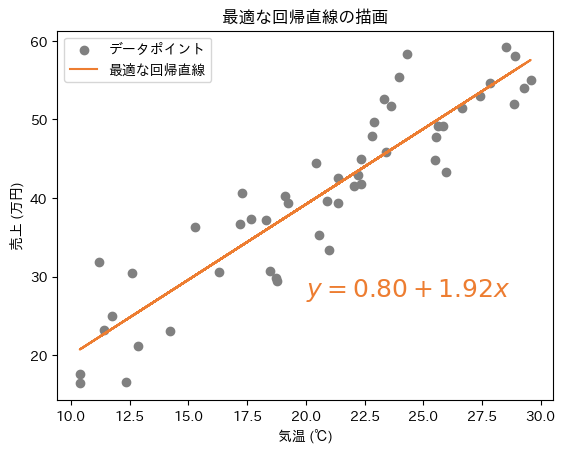 図12 仕組みの理解: 散布図上に描画した最適な回帰直線
図12 仕組みの理解: 散布図上に描画した最適な回帰直線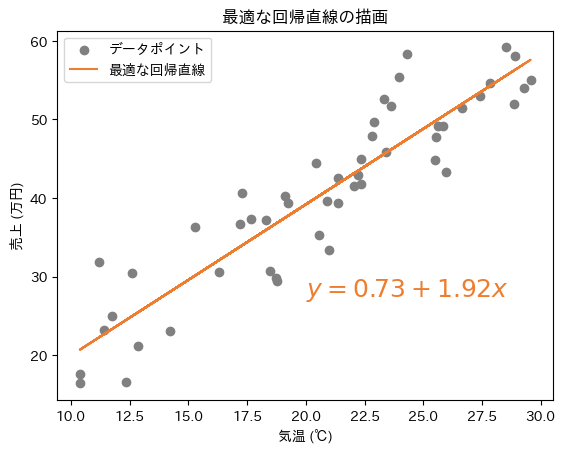 図13 仕組みの理解: 解析的に解いた場合の回帰直線
図13 仕組みの理解: 解析的に解いた場合の回帰直線