画像/動画データのディープラーニングの本質が視覚的に分かる「スカラ」「ベクトル」「行列」「テンソル」の基礎知識:「AI」エンジニアになるための「基礎数学」再入門(11)
AIに欠かせない数学を、プログラミング言語Pythonを使って高校生の学習範囲から学び直す連載。今回は「スカラ」「ベクトル」「行列」「テンソル」について、数式を使わずに図版とPythonコードで解説します。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
AIに欠かせない数学を、プログラミング言語Pythonを使って高校生の学習範囲から学び直す本連載『「AI」エンジニアになるための「基礎数学」再入門』。前回は「ベイズの定理」を学びました。今回のテーマ「スカラ」「ベクトル」「行列」「テンソル」は、数学でよく出てくる用語であり、AI(人工知能)が行う計算でもたびたび使われます。「ベクトルやテンソルとは何か」を数式を使わずに説明します。
スカラ、ベクトル、行列
まずは、スカラやベクトル、行列が何を意味しているのかを説明します。特に難しいことはありません。これらは単にデータの集まりの呼称です。構造によって、データの集まりがベクトル、行列といった呼び方に変わるだけです。これらの呼称でデータのまとまりを簡潔に表すことで、複数の値や変数でも、AIが計算で使わずに数式を簡潔に表現できます。またAIでも使われている数学では、データの集まりをこのように呼ぶことが多いので、ぜひ慣れてください。データの集まりの呼称がどのようなルールに従って変わるのか、順を追って説明します。
スカラ
スカラ(scalar)は、「1」「-3」「5.7」といった、データが1つの値であるときの呼称です。単なる数値をスカラと呼ぶときは、複数の数値で構成されるベクトルや行列と区別するのに使われ、「気温27℃」や「質量36kg」などの単一の数値で表されるものは全てスカラです。
下記はPythonでスカラを表したコードです。
a = 1 b = -3 c = 5.7 temperature = 27 mass = 36
ベクトル
ベクトル(vector)と聞くと、「高校で学習した平面上の矢印」をイメージする方が多いと思います。矢印のベクトルは、主に物理学で使われており、「大きさと向き」といった2つの要素を持つ「物理量」として定義されています。一方、AIでも使われている、数学におけるベクトルは「ひとまとまりの数字を縦か横に並べたものの呼称」と理解して問題ありません。スカラとの違いは「複数の数値で構成できること」です。スカラは単一の数値なので、ベクトルは「スカラを一方向に並べたもの」といえます。
例えば「田中」「佐藤」「山田」の3人の年齢をそれぞれ個別に表すと、それらはスカラですが、各年齢を1つの集まりとして表現する場合、その年齢データという共有の要素の集まりはベクトルになります。
Pythonでベクトルを表すには多くの場合、「NumPy」を使います。下記は、そのコードです。
import numpy as np # それぞれの年齢はスカラ Tanaka = 27 Satou = 33 Yamada = 42 # 年齢をまとめたベクトル Age_vector = np.array([27,33,42])
ベクトルの利点は「複数のデータに対する計算処理が可能」なことです。スカラで3人の年齢の平均値を計算する場合、下記のように記述する必要があります。
# スカラでの計算 (Tanaka + Satou + Yamada ) / 3
ベクトルを使うと、Pythonでは下記のように簡単に計算できます。
# ベクトルでの計算 np.mean(Age_vector)
例として3人の場合を考えましたが、これが100人、1000人となった場合でも上記のコードで簡単に算出できるのが、ベクトルのメリットです。Pythonでは、ベクトルを「1次元の配列」と呼びます。「1次元」とは、スカラが一方向に並べられていることに起因します。この名付け方に倣うと、スカラは「0次元の配列」です。
また、スカラを一方向に並べたものがベクトルですが、並べる方向が横の場合は「行ベクトル」、縦の場合は「列ベクトル」と呼びます。先ほど例示したベクトルは明示的に両者を区別しませんでしたが、Pythonでは下記のように記述することで両ベクトルを表せます。
# 行ベクトル row_vector = np.array([[1, 2, 3]]) # 列ベクトル col_vector = np.array([[1, 2, 3]]).T # 行ベクトルを表示 print(row_vector) [[1 2 3]] # 列ベクトルを表示 print(col_vector) [[1] [2] [3]]
行列
スカラを一方向に並べたものがベクトルなら、スカラを縦横2方向に並べたものが行列です。また縦ベクトルを横方向に、または横ベクトルを縦方向に並べたものなので、行列はある共有の成分でそろえた一覧表です。
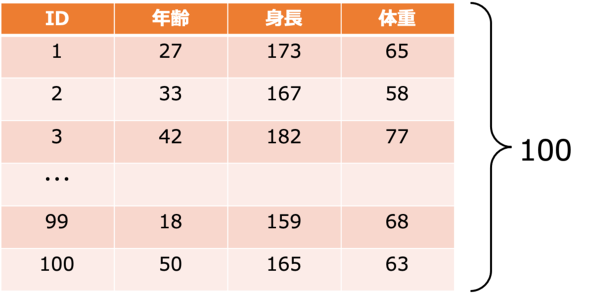
例として下図を見てください。
この行列は身体測定の結果を、IDはそれぞれ個別の人を表しています。この行列を列で見ると、「ID」「年齢」「身長」「体重」といった共有の要素ごと、つまり列ベクトルに分解できます。このIDや年齢、身長、体重の列ベクトルを横につなげたものが行列といえます。このとき、「100次元のベクトルが4つである」ことから「100×4の行列」と呼びます。行列を呼ぶ際は、行→列の順にその要素数を数えると覚えておいてください。
また行方向に別の見方をすると、別の要因で分解できます。IDごとに行で分解すると、測定した人ごとのデータのまとまりになります。これは個人ごとの測定結果ベクトルであり、この行ベクトルを縦につなげたものが行列ともいえます。この場合でも、行数は100で列数が4なので「100×4の行列」となります。
Pythonで行列を定義するときは下記のように記述します。
matrix = np.array([[1, 2, 3], [4, 5, 6] ,[7, 8, 9]]) # matrixを表示 print(matrix) [[1 2 3] [4 5 6] [7 8 9]]
上記コードでは行数3、列数3の「3×3の行列」を定義しています。Pythonで行列は「2次元の配列」のことです。「2次元」とはスカラが縦横の2方向に並べて定義されることに起因しています。
テンソル
ここまでで、スカラやベクトル、行列は「特定のルールに従って定義されているデータの集まりの呼称」と理解できたと思います。ベクトルが1次元(1方向)、行列が2次元(2方向)に並べられたデータのまとまりとするなら、3次元、4次元などに拡張できることが考えられるでしょう。このような高次元データの集まりがテンソルです。厳密には、テンソルには「データの集まり」以上の定義がありますが、AIで使う数学の知識に限定するなら、ここで説明する範囲の理解で問題ありません。
またテンソルは、3次元以上の配列に限定するものではありません。スカラやベクトル、行列などもテンソル表記で表せます。テンソルの理解で重要なことは次元が増えるごとにデータが持つ特徴量(情報量)が増えている点です。AIで複雑な計算をするには、インプットとしてAIに与えるデータもより多くの情報を必要とします。つまり、AIの種類によってインプットとするテンソルデータが異なり、目的に応じてデータの構造を変える必要があるのです。
| 次元数 | 名称 | テンソル表記 |
|---|---|---|
| 0 | スカラ(0次元の配列) | 0階のテンソル |
| 1 | ベクトル(1次元の配列) | 1階のテンソル |
| 2 | 行列(2次元の配列) | 2階のテンソル |
| 3 | 3次元の配列 | 3階のテンソル |
| 4 | 4次元の配列 | 4階のテンソル |
| …… | …… | …… |
| n | n次元の配列 | n階のテンソル |
ベクトルや行列などは直感的に理解できると思いますが、3次元配列や4次元配列であるテンソルがどのようなものか理解するのは難しいかもしれません。もっと具体的に説明します。
9〜20時で営業している果物屋の5日分の販売データを例にします。1日当たり9〜20時の計12時間分の列数で3つの果物ごとに販売数が存在するとしましょう。ある特定の日に限定すると、その日の販売データの集まりは「12×4の行列」になります。この行列データを5日分集めることで、3階のテンソルとして表せます。このときのデータ形状は「(5,12,4)」といった順で表します。
「テンソルデータでは次元が大きいと特徴量(情報量)が多い」と先述しました。テンソルデータの次元を下げることで、特徴量を減らしたデータ構造に変換できます。
例として、先ほどの3階のテンソルを行列に変換することを考えます。「日ごとの変化」を考えずに「営業時間での販売データ」が欲しい場合、5日分の販売データで平均を計算することで営業時間と各果物の行列データを取得できます。また「営業時間での変化」を考えずに「日ごとのデータ」が欲しいときは、「営業時間での累計販売データ」を計算することで、「日ごとの行列データ」と「各果物の行列データ」を取得できます。
AIはアウトプットの目的に応じてさまざまな種類があり、それぞれのAIに対して要求されるインプットのデータ構造もさまざまです。そのため、扱うAIに適したデータ構造のテンソルデータに変換する必要があります。
Pythonではテンソル(3階のテンソル)を下記のように記述します。このテンソルの形状は「(2,3,4)」です。
tensor = np.array([
[
[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]
],
[
[13, 14, 15, 16],
[17, 18, 19, 20],
[21, 22, 23, 24]
],
])
# データの形状を表示
print(tensor.shape)
# (2, 3, 4)
「高階のテンソルデータ」を扱うモデルが「ディープラーニング」
最後に、高次元で特徴量を多く含んだテンソルデータ「高階のテンソルデータ」について触れていきます。一般的に高階のテンソルデータを扱うのは難しいことですが、このデータ構造に特化したAIは、より表現力の高いアウトプットを出すことができます。インプットとして高階のテンソルデータを使うAIには「ディープラーニング」というモデルが存在します。以降では、ディープラーニングに使われる高階のテンソルデータの一例を紹介します。
画像データ(4階のテンソル)
高階のテンソルデータの例として「画像データ」があります。白黒画像1枚には縦横の2方向にピクセル(pixels)が存在し、各ピクセルに光量の大きさが数値として記録されています。解像度が256×256ピクセルの場合、画像1枚は「256×256の行列」データです。画像が複数存在する場合、このデータの集まりは3階のテンソルです。128枚あるとすると、そのデータ形状は「(128,256,256)」です。さらに白黒ではなく赤、緑、青の色を持つRGB(Red、Green、Blueの頭文字)カラー画像の場合、そのデータは4階のテンソルであり、そのデータ形状は「(128,256,256,3)」です。
動画データ(5階のテンソル)
複数の動画データだと、さらに次元が増えます。解像度が256×144ピクセルの60秒のカラー動画を例として考えてみましょう。動画が30フレーム(1秒当たりで処理するコマ数)だった場合、1つの動画データで必要な画像データは1800(30×60)枚です。つまり、1つの動画で4階のテンソルです。動画が2つある場合は、さらに次元が増えて5階のテンソルであり、そのデータ形状は「(2,1800,256,144,3)」です。
まとめ
下記は今回のまとめです。
- データの持つ次元数に応じてそのデータ構造に対する呼称があり、ベクトルや行列は、その一部
- AIのタイプに応じて要求するデータ構造が異なり、それぞれに適応した次元数のテンソルデータに変換する必要がある
- 画像や動画といった高階のテンソルデータを扱うAIとしてディープラーニングがある
筆者紹介
原 拓自(はら たくじ)
1988年、岐阜県生まれ。大学院では宇宙物理を専攻し、卒業後はデータサイエンティストとしてキャリアをスタートする。
さまざまな会社で分析コンサルを経験した後、世界最大の外資系ECサイト会社でデータサイエンスの知識を深める。
現在は東京ITスクールの講師として、実務レベルのデータサイエンティスト輩出を目的としたAI研修に努める傍ら、分析や機械学習を用いたマーケティング支援を行う。
西村圭介
1991年、富山県生まれ。大学院を卒業し、企画コンサルタントとしてキャリアをスタートする。その後、統計学とプログラミングスキルの知見を基にデータサイエンティストとしてのキャリアを進める。現在は東京ITスクールの講師として、実務レベルのデータサイエンティスト輩出を目的としたAI研修に努める傍ら、分析や機械学習を用いたマーケティング支援を行う。
関連記事
 Lesson 1 機械学習を始めるための、Pythonデータ構造「多次元リスト」入門
Lesson 1 機械学習を始めるための、Pythonデータ構造「多次元リスト」入門
Pythonの基本的な言語仕様では、データはどう表現できるのか? 単一の数値データから始め、1次元、2次元、……多次元と複数の数値データを表現できるリスト型のデータ構造まで、ステップ・バイ・ステップで見ていく。 第3回 TensorFlowの基本構成要素:「テンソル」と「セッション」
第3回 TensorFlowの基本構成要素:「テンソル」と「セッション」
TensorFlowによる深層学習を始める前に、TensorFlowの基本的な構成要素であるテンソルとセッションを理解しておこう。TensorFlowのコード例を示しながら、できるだけコンパクトにまとめる。 機械学習の基礎の基礎、行列計算に欠かせないNumPyの基本的な使い方
機械学習の基礎の基礎、行列計算に欠かせないNumPyの基本的な使い方
最近流行の機械学習/Deep Learningを試してみたいという人のために、Pythonを使った機械学習について主要なライブラリ/ツールの使い方を中心に解説する連載。今回は、科学的計算の基本的パッケージNumPyを使って、配列の基本操作、スライシングとインデクシング、配列を使った簡単な計算の仕方などを紹介。
Copyright © ITmedia, Inc. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ