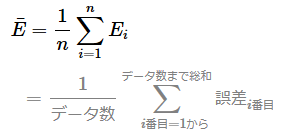［評価関数］分散説明率（Explained variance score）とは？：AI・機械学習の用語辞典

用語「分散説明率」について説明。線形回帰モデルなどの評価関数の一つで、回帰式のモデルが「観測データの分散」のうちどれくらいの割合を説明するかを表す。決定係数R2の代わりに用いられることがある。

» 2021年10月21日 05時00分公開

[一色政彦，デジタルアドバンテージ]

用語解説

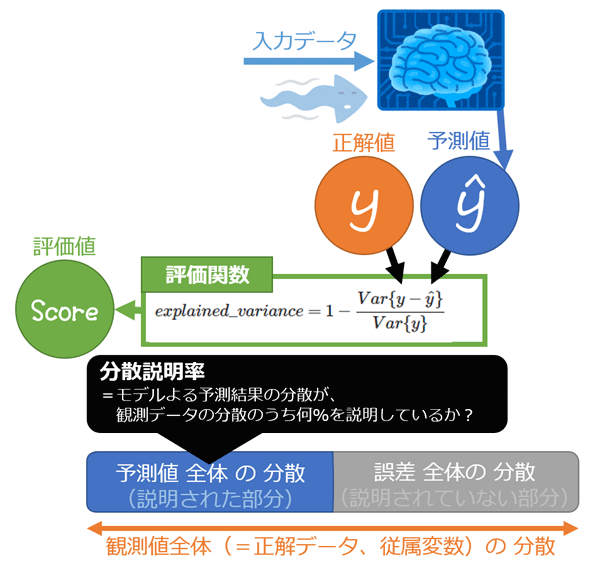
　統計学／機械学習における分散説明率（explained variance score：説明された分散のスコア、explained variation）とは、主に単回帰分析／重回帰分析といった線形回帰（Linear Regression）*1における回帰式のモデルなどが、「観測データ（正解データ、従属変数、目的変数）*2の分散（＝データの広がり具合）のうちどれくらいを説明するか」という割合（通常は0～1.0＝100％、マイナスになることもある）を出力する関数である（図1）。決定係数R²の代わりに用いられることがある。

*1　統計学に基づく線形回帰モデルに入力する各種データは「説明変数」や「独立変数」と呼ばれ、これが機械学習での「入力データ」となる「特徴量」に相当する。また線形回帰モデルでは、モデルから出力される「予測値」は「目的変数」や「従属変数」と呼ばれる。本稿の趣旨から逸脱するのでごく簡略的に示すと、線形回帰のモデルは、説明変数（例えばx₁とx₂）と目的変数（例えばy）を用いてy＝ax₁＋bx₂＋cのような式で表現でき、最適化によってパラメーターa／b／cを決定する。

*2　機械学習で「（教師）ラベル」や「正解値」などと呼ぶものは、統計学においては「観測値（observed value）」や「実測値」「実際の測定値」などと呼ばれることが一般的である。

図1　「分散説明率」のイメージ

定義と数式

　前提条件としてまず、「観測値（＝正解値、従属変数、目的変数）」と「モデルによる予測値」の誤差（もしくは残差）を計算する式は次の通りだ。

　また前提条件として、全データに対する全ての誤差の平均値は次のような計算式になる。

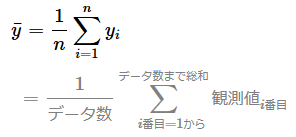
　同様に、全観測データの平均値を計算する式は次のようになる。

　以上の前提条件を踏まえると、分散説明率（explained variance score）を計算する式は次のように表現できる。データ数で割る1/nの計算は打ち消し合って全て消せるので、よりシンプルな式で表現できる。

　1（＝100％）から「誤差全体の分散」の割合（＝「観測値全体の分散」で割った値）を引くことで、「予測値全体の分散」の割合が求まる。前掲の図1にも示したように、「予測値全体の分散」は、「観測値全体の分散」のうちモデルによって説明された部分を意味する。

用途と、決定係数R2との違い

　分散説明率は、既に述べた通り、主に線形回帰の評価関数として用いられる。関数から出力される値は、1に近いほどより良い。

　決定係数R²と分散説明率の数式を見比べてみよう。

　基本的に同じような式になっているが、一部異なる箇所がある。具体的には、決定係数R²で「観測値_i番目－予測値_i番目」となっている箇所が、分散説明率では「誤差_i番目－誤差全体の平均値」となっている点が異なる。前述の「定義と数式」の最初に示したように「誤差_i番目」＝「観測値_i番目－予測値_i番目」なので、厳密には分散説明率では「－誤差全体の平均値」という計算が追加されているという点が異なるわけだ。ちなみに、試しに「誤差（＝正解値と予測値の差、残差）全体の平均値」が0になるデータで計算してみると、決定係数R²と分散説明率は全く同じ値となることが確認できるはずだ。

　要するに基本的には、決定係数R²と分散説明率は同じように使える。ただし分散説明率では、「誤差全体の平均値を減算する計算」が追加されることによって、誤差が中心化されてより良い評価値が出やすいという特徴がある。特にモデルによる予測値と正解値の誤差に偏り（バイアス）がある場合には、決定係数R²だけでなく分散説明率もチェックする、といった使い方が考えられるだろう。