分散(Variance)/標準偏差(SD:Standard Deviation)とは?:AI・機械学習の用語辞典
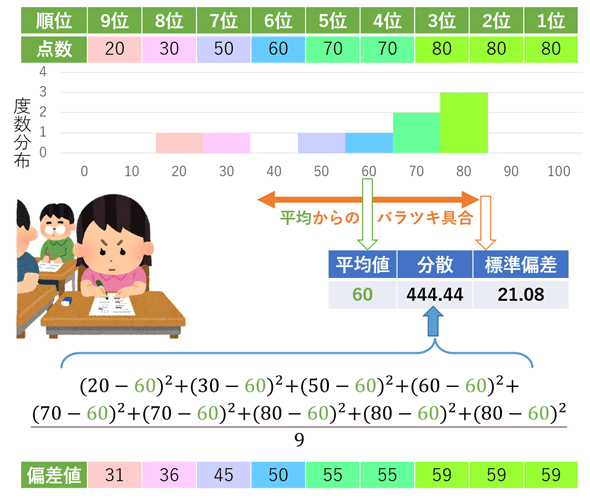
用語「分散」「標準偏差」について説明。いずれもデータの広がり具合を表す統計量。分散は、各データに対して「平均値との差」(=偏差)の二乗値を計算し、その総和をデータ数で割った値(=平均値)を表す。標準偏差は、分散に対する平方根の値を表す。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
用語解説
数学/統計学/機械学習における分散(variance)とは、データ(観測値)がどれくらい広がっているか、より厳密には「データが平均値からどれくらい離れているか」(=バラツキ具合)を表す統計量である。分散は、各データに対して「(全データから計算した)平均値との差」(=「偏差:deviation」と呼ぶ)の二乗値を計算し、その二乗値の総和をデータ数で割ること(つまり全二乗値の平均値)で求まる(数式は後述)。
標準偏差(SD:Standard Deviation)とは、分散に対する正の平方根(√)の値のことで、単位を二乗値から元に戻している。つまり、分散と標準偏差は単位が異なるだけで、同じものを表す統計量となる。
使い分け指針
数学や統計学で扱う分には、分散の方が、二乗値のまま計算を続けられるので扱いやすい。一方で、人間が理解したり人に説明したりする場合には、標準偏差の方が、単位が元に戻っているので分かりやすい。そこが両者の使い分けポイントとなる。
ちなみに標準偏差を応用した身近な評価指標に「偏差値」がある。テストを受けた集団の中で、各受験者の立ち位置がどれくらいかを把握するために使われている。偏差値とは、平均点からの偏差(=中心化した値)を標準偏差で割って標準化した値(=〜±1.0〜±2.0〜といった小さな値になる)を、人間がより扱いやすいように10倍し、さらに(例えば−10のようなマイナスの値を避けるために)50を足すことで値の中心を0から50に動かした値である。
「分散」の定義と数式
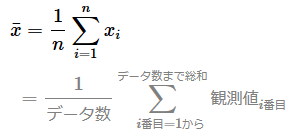
前提条件として、全データから平均値を計算する式は次のようになる。統計学に寄せて「観測値(observed value)」と表記したが、「実測値」「実際の測定値」の他、さまざまな方法で収集したデータがこの対象となる。
分散(σ2)の数式は、上記の平均値の式を使って以下のように定義できる。
「標準偏差」の定義と数式
標準偏差(σ)の数式は、分散の式に平方根(√)を付けるだけである。
MSE/RMSEとの違い
分散/標準偏差の数式を見て、平均二乗誤差(MSE:Mean Squared Error)/RMSE(MSEの平方根)とほぼ同じ数式であることに気づいたかもしれない。確かに、分散とMSE、標準偏差とRMSEの数式は酷似している。しかしこれらは同じではないので注意してほしい。どこが違うかというと、まず用法も違うが、使われる変数が異なる。
- 分散/標準偏差: 単一の変数(例えば数学テストの点数)において、データが平均からどれくらい広がっているかを調べるために用いられる
- MSE/RMSE: モデルからの予測値(例えば予測した家賃)と正解値(例えば実際の家賃)という2つの変数の間でどれくらい差異(「損失:loss」と呼ばれる)があるかを調べるために用いられる
なお、分散/標準偏差で計算する「各データと平均値の差」は前述の通り「偏差(deviation)」と呼ばれるのに対し、MSE/RMSEで計算する「予測値と正解値の差」は「誤差(error)」と呼ばれる、といった用語の違いもある。ちなみに、統計学の残差平方和(RSS:Residual Sum of Squares)で計算する「観測値と予測値の差」は「残差(residual)」と呼ばれる。
ここを更新しました(2023年9月11日)
冒頭の説明をより分かりやすい言葉で書き直しました。
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ