［評価関数］中央絶対誤差（MedAE：Median Absolute Error）とは？：AI・機械学習の用語辞典

用語「中央絶対誤差」について説明。評価関数の一つで、各データに対して「予測値と正解値の差（＝誤差）」の絶対値を計算していき、それら全ての計算結果における中央値を表す。

» 2021年08月18日 05時00分公開

[一色政彦，デジタルアドバンテージ]

用語解説

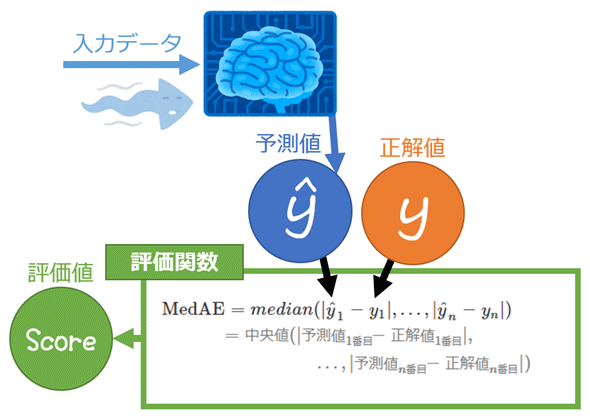
　機械学習における中央絶対誤差（MedAE：Median Absolute Error）とは、各データに対して「予測値と正解値の差（＝誤差）」の絶対値を計算していき、それら全ての計算結果を小さい順に並べた中で順位がちょうど中央に位置する値（＝中央値）を出力する関数である（図1）。なお誤差は、「予測値－正解値」ではなく「正解値－予測値」でもよい。

図1　「中央絶対誤差」のイメージ

　MAE（平均絶対誤差）と名前が紛らわしいため、本稿では「MedAE」と記載した。なお、略語で「MAE」と記載されている場合は、中央絶対誤差ではなく、平均絶対誤差を指すことが一般的である。

定義と数式

用途と特徴

　MedAEは、主に回帰問題における出力層の評価関数として用いられる。関数から出力される値は、0に近いほどより良い。

　MedAEの特徴は、中央値を使うので、外れ値に対してロバストな（＝頑健な、強い）ことである。そもそも中央値は、統計学において主に平均値が有効ではない場面、具体的にはデータの一部に大きな外れ値があるような場面で、平均値の代わりに用いられる（※大きな外れ値を含むデータを平均すると、どうしても大きな値の方向に引きずられてしまうため）。同様にして、機械学習モデルによる予測値（あるいは正解値）の一部に大きな外れ値が含まれるような場面で、MAE（平均絶対誤差）の代わりに、MedAE（中央絶対誤差）を使うことが考えられる。

　とはいえ機械学習でMedAEを使うことはあまりない。筆者の経験では、Azure Machine Learningの自動ML（Automated ML、AutoML）の評価指標として自動計算されたことがあるくらいだ（参考：「AutoML 実験結果の評価 - Azure Machine Learning | Microsoft Docs」）。ちなみに統計学では、（詳細は割愛するが）MedAEに類似の中央絶対偏差（Median Absolute Deviation：MAD）という評価指標があり、主にロバスト統計学／ロバスト回帰で用いられている。