平均絶対偏差（Mean Absolute Deviation）／中央絶対偏差（Median Absolute Deviation）とは？：AI・機械学習の用語辞典

用語「平均絶対偏差」「中央絶対偏差」について説明。いずれもデータの広がり具合を表す統計量。平均絶対偏差は、各データに対して「平均値との差」（＝偏差）の絶対値を計算し、その総和をデータ数で割った値（＝平均値）を表す。中央絶対偏差は、各データに対して「中央値との差」（＝偏差）の絶対値を計算し、その全ての絶対値から求めた中央値を表す。

[一色政彦，デジタルアドバンテージ]

連載目次

用語解説

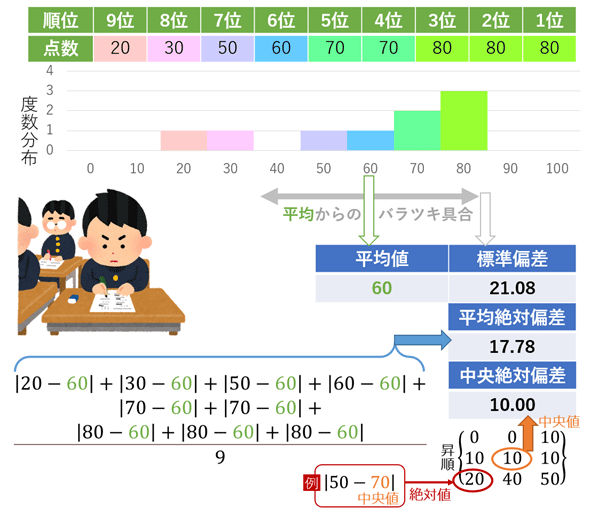
　数学／統計学／機械学習における平均絶対偏差（MAD：Mean Absolute Deviation）とは、データ（観測値）の広がり具合、より厳密には「平均値」からのバラツキ具合を表す統計量で、各データに対して「（全データから計算した）平均値との差」（＝「偏差：deviation」と呼ぶ）の絶対値を計算し、その絶対値の総和をデータ数で割った値（つまり全絶対値の平均値）のことである。平均偏差や絶対偏差という略名で呼ばれることもある。

　中央絶対偏差（MedAD：Median Absolute Deviation）とは、「中央値」からのバラツキ具合を表す統計量で、各データに対して「（全データから計算した）中央値との差」（＝偏差：deviation）の絶対値を計算し、その全ての絶対値から求めた中央値のことだ。

図1　平均絶対偏差／中央絶対偏差のイメージ

使い分け指針：平均絶対偏差／中央絶対偏差の違い

　「平均」絶対偏差と「中央」絶対偏差の違いは、平均値と中央値の違いに等しい。つまり、通常は「平均」を使えばよいが、外れ値の影響を排除したい場合には「中央」を使えばよい。詳しくは「平均値（Mean）／中央値（Median）／最頻値（Mode）とは？」を参照してほしい。

　平均絶対偏差／中央絶対偏差の欠点として、絶対値は微分などの数学計算がしづらいという問題がある。このため通常は、平均絶対偏差／中央絶対偏差ではなく、同じく「データの広がり具合を表す統計量」である分散（Variance）／標準偏差（SD：Standard Deviation）が用いられる。これに関連して、分散／標準偏差との使い分け指針も示しておく。

使い分け指針：分散／標準偏差との違い

　前提として分散／標準偏差では偏差の「二乗値」を計算するが、平均絶対偏差／中央絶対偏差では偏差の「絶対値」を計算するという違いがある。分散は、二乗するため元の数値と単位が変わってしまうので（例えば元の数値「1」を2乗すると→出力結果は「1」、10の2乗→100、100の2乗→10,000と大きく単位が変化するので）、人間にとってシンプルに理解するのが難しいという問題がある。一方、平均絶対偏差／中央絶対偏差は、絶対値しか計算しないので元の数値から単位が変化せず、人間にとってシンプルで理解しやすいという利点がある。人間にとって解釈しやすいことを重要視するならば、分散ではなく単位を元に戻した標準偏差か、この平均絶対偏差／中央絶対偏差を使えばよいだろう。

　さらに平均絶対偏差／中央絶対偏差には、標準偏差よりも外れ値の影響を受けにくい（＝ロバストである）という利点もある（これも一度も二乗しておらず単位が変わっていないことの恩恵）。外れ値へのロバスト性（頑健性）は次のような順位になる。

ロバスト性： （低い）　標準偏差　＜　平均絶対偏差　＜　中央絶対偏差　（高い）

　この順位を実際の数値で確認するために筆者が手元で、平均0.0、分散1.0の正規分布でランダムな数値を50個生成したデータセットと、同じデータに10という外れ値を追加したデータセットのそれぞれで、標準偏差／平均絶対偏差／中央絶対偏差の数値を求め、両データセット間の比率を計算してみた。その結果、標準偏差＝1.84倍、平均絶対偏差＝1.28倍、中央絶対偏差＝0.99倍となった。これらの数値を見ると、標準偏差は外れ値に大きく引っ張られており、平均絶対偏差はそこそこ引っ張られており、中央絶対偏差は引っ張られていない（※乱数生成なので多少の誤差はある）ことが分かる。

　以上の特徴から、中央絶対偏差は、主にロバスト統計学／ロバスト回帰で用いられている。

「平均絶対偏差」の定義と数式

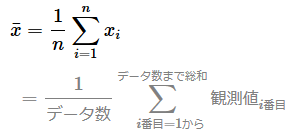
　前提条件として、全データから平均値を計算する式は次のようになる。統計学に寄せて「観測値（observed value）」と表記したが、「実測値」「実際の測定値」の他、さまざまな方法で収集したデータがこの対象となる。

　平均絶対偏差（MAD）の数式は、上記の平均値の式を使って以下のように定義できる。

「中央絶対偏差」の定義と数式

　前提条件として、全データから中央値を計算する式は次のようになる。

　中央絶対偏差（MedAD）の数式は、上記の中央値の式を使って以下のように定義できる。

平均絶対誤差／中央絶対誤差との違い

　平均絶対偏差／中央絶対偏差の数式を見て、平均絶対誤差（MAE：Mean Absolute Error）／L1損失や中央絶対誤差（MedAE：Median Absolute Error）とほぼ同じ数式であることに気づいたかもしれない。確かに、平均絶対偏差と平均絶対誤差、中央絶対偏差と中央絶対誤差の数式は酷似している。しかしこれらは同じではないので注意してほしい。どこが違うかというと、まず用法も違うが、使われる変数が異なる。

• 平均絶対偏差／中央絶対偏差： 単一の変数（例えば数学テストの点数）において、データが平均／中央からどれくらい広がっているかを調べるために用いられる
• 平均絶対誤差／中央絶対誤差： モデルからの予測値（例えば予測した家賃）と正解値（例えば実際の家賃）という2つの変数の間でどれくらい差異（「損失：loss」と呼ばれる）があるかを調べるために用いられる

　なお、平均絶対偏差／中央絶対偏差で計算する「各データと平均値／中央値の差」は前述の通り「偏差（deviation）」と呼ばれるのに対し、平均絶対誤差／中央絶対誤差で計算する「予測値と正解値の差」は「誤差（error）」と呼ばれる、といった用語の違いもある。ちなみに、統計学の残差平方和（RSS：Residual Sum of Squares）で計算する「観測値と予測値の差」は「残差（residual）」と呼ばれる。

「AI・機械学習の用語辞典」