積分法の数値計算をプログラミングしてみよう:数学×Pythonプログラミング入門(1/5 ページ)
積分法に関する数値計算のプログラミングの方法を見ていく。最初に台形公式やシンプソンの公式を使った方法を紹介し、次に乱数を使ったモンテカルロ法による近似方法を見る。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
前回は、微分法の数値計算を行いました。今回は、積分の数値計算法を見ていきます。まず、高校で学んだ台形公式を使った積分の数値計算を行い、次により精度のよいシンプソンの公式を使った数値計算を行います。また、乱数を使ってデータのサンプリングを行うモンテカルロ法も紹介します。Pythonの文法やライブラリに関してはNumPyのlinspace関数の利用と、乱数の利用を取り上げます。
今回の練習問題としては、正規分布の−2σ〜2σ までの累積確率を求めるプログラム、曲線の長さを求めるプログラム、マルコフ連鎖モンテカルロ法(メトロポリス法)による正規分布のサンプリングを行うプログラムを取り上げます。
上に記した各種の方法は、中学・高校の数学で全て理解できるものです。聞き慣れない用語が幾つか登場しているかもしれませんが、実際のところ面積や割合を求めるために総和の計算をしているだけです。気軽に読み進めてください。
連載:
『数学×Pythonプログラミング入門 ― 中学・高校数学で学ぶ』
この連載では、中学や高校で学んだ数学を題材にして、Pythonによるプログラミングを学びます。といっても、数学の教科書に載っている定理や公式だけに限らず、興味深い数式の例やAI/機械学習の基本となる例を取り上げながら、数学的な考え方を背景としてプログラミングを学ぶお話にしていこうと思います。
筆者紹介: IT系ライター、大学教員(非常勤)。書道、絵画を経て、ピアノとバイオリンを独学で始めるも学習曲線は常に平坦。趣味の献血は、最近脈拍が多く98回で一旦中断。
目標1: 台形公式を使って積分を行う
積分(定積分)は、微小な値の総和を求めることと考えられます。それにより、面積が求められるということは高校の数学で学んだ通りです。積分は、確率密度関数を基に、累積確率を求める場合などにも使われます。まずは、ごく簡単な例を使って積分の数値計算を行ってみましょう。
例えば、以下のような定積分を考えてみます。
これは、図1に示したy=x2のグラフとx軸の0〜1で囲まれるアミカケの部分の面積を求める計算にほかなりません。
解析的に積分の計算を行うと、
となります。しかし、このような式の変形ができなくても面積を求めることはできます。
というわけで、この積分の近似計算を行ってみましょう。まずは台形公式を使ってやってみます。なお、今回のサンプルプログラムについても、紹介動画を用意してあります。ただし、コードを1行1行解説しているわけではなく、作成から実行までの流れを紹介したものなので、全体像と実行結果を確認するのにご利用ください。
動画1 積分の近似計算
コラム 定積分の計算方法
積分のための式の変形ができなくても数値計算はできますが、ここで簡単に解説しておきます。読み飛ばしていただいても構いませんが、高校で学んだ数式の意味や書き方を思い出したい方は確認しておいてください。
をxで積分することを以下のように書きます。∫は「インテグラル」と読みます。積分した結果もxの関数になるので、それをF(x)と表しておきます。
積分は微分の逆の計算です。微分の場合は、指数を係数に掛け、指数の値を1減らしました。その逆なので、指数を1増やして、「1/指数」を係数に掛ければ、簡単に計算ができます。上の例であれば、xの指数が2なので、3乗にして、1/3を掛けます。Cは定数項です。Cの値はどんな値であっても構いません(右辺を微分すると定数項のCは消えてしまいます)。
この式ではCの値が決まらないので「不定積分」と呼ばれます。また、F(x)は原始関数と呼ばれます。
積分を行うxの範囲が決まっている場合は「定積分」と呼ばれ、
のように、∫の下に下限値(数学用語では「下端」と呼ばれます)を書き、上に上限値(数学用語では「上端」と呼ばれます)を書きます。この場合、原始関数のxに上限値を代入した式からxに下限値を代入した式を引くと、定積分の値が求められます。
なお、F(b)−F(a)のことを、
と書きます。
1. 台形公式による積分をプログラミングする
台形公式による積分とは、求めたい面積を、グラフを図2のような細かい「短冊」に分け、それらを全て足すという方法です。短冊の形はほぼ台形になっているので、小学校のときに学んだ台形の面積の公式「(上底+下底)×高さ÷2」が使えます。
図2を見れば、アミカケの部分は台形を90°回転させたような形になっており、f(x)が上底、f(x+h)が下底、hが高さに当たることが分かります。xを0から1まで変えながら、hを0.001として、台形の面積を全て足し、全体の面積を求めてみましょう。
刻み値を指定する方法
まず、y=x2のグラフを関数parabolicとして定義しておきます。これは簡単ですね(リスト1)。
def parabolic(x):
return x**2
y=x2のグラフは放物線(parabolic)を描く。x2の値を返すだけなので関数の定義は簡単。
続いて、指定した関数のxminからxmaxまで、h刻みで台形の面積を求め、それらの総和を求める関数integralを定義します(リスト2)。
import numpy as np
def integral(func, xmin, xmax, h):
result = 0
for x in np.arange(xmin, xmax, h):
result += (func(x) + func(x+h)) * h / 2
return result
funcには面積を求めたい関数の参照を指定する。xminは下限値、xmaxは上限値、hは刻み値となる。関数の内容は「(上底+下底)×高さ÷2」という台形の公式をそのままコードとして表し、xの値をhずつ動かしながら合計していくだけ。
これまでの連載で学んだ知識だけで全てできますね。では、実行してみましょう。
integral(parabolic, 0, 1, 0.001)
# 出力例:0.33333349999999984
解析的に求めた答えは1/3なので、0.333...に近い値になれば正解。
範囲を幾つに分けるかを指定する方法
台形公式による積分は簡単でした。上の例では、刻み値hを指定しましたが、全体を幾つに分けるかを指定するなら、リスト4のようになります。
import numpy as np
def integral2(func, xmin, xmax, count):
result = 0
xdata, h = np.linspace(xmin, xmax, count, endpoint=False, retstep=True)
for x in xdata:
result += (func(x) + func(x+h)) * h / 2
return result
関数integral2では、最後の引数を「刻み値」ではなく、範囲を幾つに分割するかという値に変更した。NumPyのlinspace関数を使って等差数列を作る。
この例では、NumPyのlinspace関数を使って、等差数列を作成しています。linspaceは「リンスペース」と読むことが多いようですが、その説明は後回しにして、先に実行しておきましょう。0から1までの範囲を1000個に分けて計算してみます(リスト5)。
Integral2(parabolic, 0, 1, 1000)
# 出力例:0.33333349999999984
リスト2と同じ計算になるので、結果も当然同じ。
NumPyのlinspace関数の使い方
では、NumPyのlinspace関数の使い方を見ておきましょう。
linspace関数(引数にstart/stop/num/endpoint/retstepなどがある)は、下限値(start)から上限値(stop)までを、num個に分けた数列を作ってくれます。具体例で見てみます(リスト6〜8)。以下のどの例も、すでにimport numpy as npが書かれているものとします。
np.linspace(0, 1, 10)
# 出力例:
# array([0. , 0.11111111, 0.22222222, 0.33333333, 0.44444444,
# 0.55555556, 0.66666667, 0.77777778, 0.88888889, 1. ])
0以上1以下を10個に分けた場合の実行例。刻み値は0.1ではなく、0.111...となることに注意。
注意すべき点は、上限値が含まれるということです。上限値を含めたくない場合は、引数にendpoint=Falseを指定します。
np.linspace(0, 1, 10, endpoint=False)
# 出力例:
# array([0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9])
0以上1未満を10個に分けた場合の実行例。刻み値は0.1となる。
さらに、刻み値が幾つになるかを知りたいときには、引数にretstep=Trueを指定します。
np.linspace(0, 1, 10, endpoint=False, retstep=True)
# 出力例:
# (array([0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9]), 0.1)
0以上1未満を10個に分けた場合の実行例。刻み値は0.1となる。数列と刻み値のタプルが返される。
数列と刻み値はタプルとして返されるので、数列をxdataに、刻み値をhに代入したければ、
xdata, h = np.linspace(0, 1, 10, endpoint=False, retstep=True)
とします。タプルは、これまでにもさりげなく登場はしていましたが、きちんと説明していなかったので、簡単に見ておきます。タプルはリストに似ていますが、その要素の値を変更できないもので、[]ではなく()で要素を囲みます。
例えば、
a = (1, 2, 3)
のようなものがタプルです。要素を取り出すにはリストと同じ表記が使えます。
a[1]
とすると2が返されます。しかし、値は変更できないので、
a[1] = 10
とすると、エラーが表示されます。タプルは内容を変更したくない決まった値の並びを表すのに便利です。
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ


 羽山博
羽山博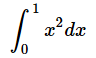
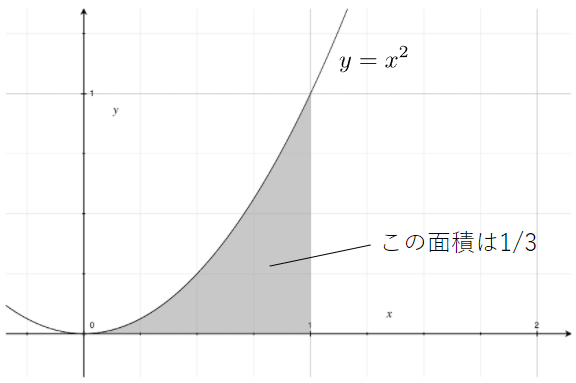 図1
図1 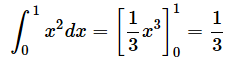
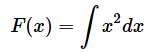
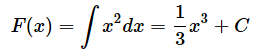
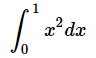
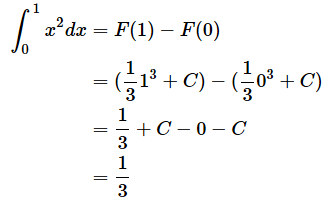
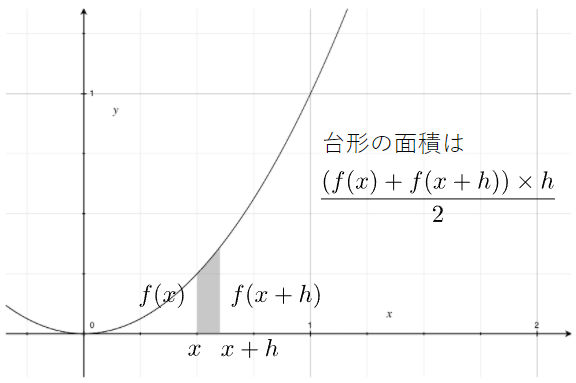 図2 求めたい面積を小さな台形に分ける
図2 求めたい面積を小さな台形に分ける



