言語モデルのスケーリング則（Scaling Laws for Neural Language Models）とは？：AI・機械学習の用語辞典

用語「スケーリング則」について説明。自然言語処理モデルのサイズ（＝パラメーター数）や、データセットのサイズ、トレーニングに使用される計算量が増えるほど、より高い性能を発揮できる、という法則を指す。

» 2023年05月24日 05時00分公開

[一色政彦，デジタルアドバンテージ]

用語解説

　物理学や生物学など幾つかの分野に「スケーリング則」（Scaling Laws）という用語があるが、本稿では人工知能／機械学習分野の自然言語処理におけるスケーリング則について紹介する。

　ニューラル言語モデル（＝ニューラルネットワークの自然言語処理モデル）における「スケーリング則（Scaling Laws for Neural Language Models）」とは、自然言語処理モデルのパラメーター数（＝モデルのサイズ）や、データセットのサイズ、トレーニングに使用される計算（Compute）量が増えるにつれて、損失（Loss、誤差）が「べき乗則」*1に従って減少する、という法則のことである（図1）。つまり、時間と費用を掛けた巨大なモデルほど、より高い性能を発揮できる、ということだ。

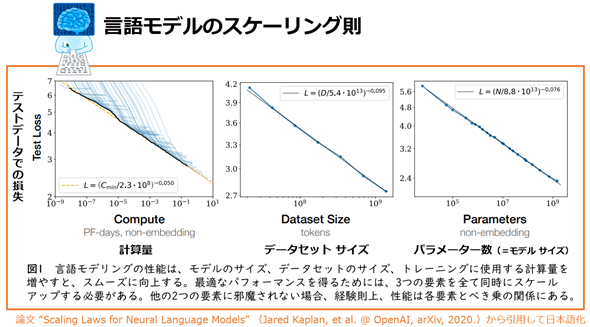図1　スケーリング則（Scaling Laws for Neural Language Models）のイメージ
引用論文“Scaling Laws for Neural Language Models”（Jared Kaplan, et al. @ OpenAI, arXiv, 2020.）

*1　「べき乗」とは、数学でxⁿ（＝xのn乗）のような式で表現でき、変数xをn回掛け合わせることだ（nが正の整数に限定できる場合は「累乗」とも呼ぶ）。べき乗は、大きすぎたり小さすぎたりする数値を人間が理解しやすく表現する際に便利で、例えば「10の1乗＝10」「10の4乗＝10,000（＝1万）」「10の8乗＝100,000,000（＝1億）」のように「○乗」の数字を少し上げ下げするだけで非常に小さな数値から非常に大きな数値までが表現できる。
　数学における「べき乗則」とは、上記のべき乗のルールにのっとっていることである。統計学などの科学分野では、ある項目が変化すると他の項目が「べき乗則」に従って変化する法則を「スケーリング則」と呼ぶことがある。例えば正方形の面積は、長さを2倍にすると4倍（＝2の2乗）に、長さを4倍にすると16倍（＝2の4乗）になるので、べき乗のルールにのっとってスケーリングしている。この面積については単純化した場合の一例だが、科学的な文脈ではより大きな数値のスケールで「べき乗則」や「スケーリング則」という用語が使われる。

　本稿で説明しているスケーリング則は、OpenAIが2020年1月に公開した論文『Scaling Laws for Neural Language Models』に基づいた内容となっている。この論文は、AIや自然言語処理の業界で話題となり、業界全体でAIモデルの巨大化が進む一因となった。

　OpenAIは、この論文の内容に従って、GPT-2よりも大規模なGPT-3やGPT-4などの言語モデルを作ってきた。しかし2023年4月、OpenAIのCEOであるサム・アルトマン（Sam Altman）氏が「巨大なAIモデルの時代はすでに終わった」と主張し、今後はスケーリング則に頼らない手法（その有望な手法の一つが「RLHF：人間のフィードバックを使った強化学習」）の採用を考えていることが報じられた（参考：「OpenAI’s CEO Says the Age of Giant AI Models Is Already Over | WIRED」）。スケーリング則のように際限なく巨大化する手法は、データセンターの構築やコストなど物理的な限界があるためだ。

　なおスケーリング則については、OpenAIの、この論文だけではなく、幾つかの他の論文からも提示されている。筆者が検索により調査した限りでは、例えば以下のようなものがヒットした。「スケーリング則」と呼ぶ場合、人や記事などによっては違う論文に基づく法則を指している可能性があることに注意してほしい。