[NumPy超入門]Pythonでのデータ処理をNumPyから始めよう!:Pythonデータ処理入門
NumPyってどんなもの? どんな機能があるの? ここからデータ処理の第一歩を踏み出そう。Python入門に続く入門シリーズが開始!
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
本シリーズと本連載について
Pythonは現在とてもよく使われるプログラミング言語の一つです。特に人工知能、機械学習、データ処理やデータ分析といった分野においてはPythonとそのライブラリはとてももてはやされています。ですが、Pythonの基礎を学んだだけで今述べたような分野に乗り出していくのは少し大変なことでもあります。
プログラミング言語だけを覚えても、その言語で何かを行うには十分ではないことはよくあります。特に複雑なことをやろうと思ったら。何かを行うためには、さまざまなライブラリやフレームワークの使い方も学ぶ必要があります。あるいは、自分でそうしたライブラリやフレームワークを構築する方法もありますが、そのためにはかなりの労力が必要となるでしょう。
何かを実現するためにその道具(ライブラリやフレームワーク)から作り始めるのは理想的です。が、例えば数値計算やデータの処理、可視化、機械学習、人工知能といった分野には既に先人たちの知恵と技術の成果があり、多くの人がそれらを使って何かを成し遂げています(もちろん他の分野でもPython向けのライブラリやフレームは充実しています。そして、そうした成果が多いことが現在のPythonの人気にもつながっているのでしょう)。
使っている人が多ければ、自分が分からないことについて調べるときにも安心です。Webを検索すれば、同じように困ったことがある人がそのことについて記録を残してくれているかもしれません(今となってはWeb検索よりもチャットボットを使った勉強の方が便利という方もいるでしょうけれど)。
本シリーズ「Pythonデータ処理入門」では「Python入門」に続くPython学習シリーズとしてPythonに関する基礎知識を備えた方々に向け、「Pythonは覚えたけど、次は何を学んで、どうやって膨大な量のデータを処理したらいいの?」というお話をしていければと思っています。
具体的には以下のようなトピックごとに数回から十数回程度の連載を通して、Pythonでデータ処理を行うために必要な知識や実際のデータ処理の方法を読者の皆さんと勉強していく予定です。
- NumPy:Pythonで数値計算や科学計算を効率的に行うためのライブラリ(本連載)
- pandas:Pythonで大量のデータの解析や処理を行うためのライブラリ
- matplotlib:Pythonで大量のデータをグラフ化/可視化するためのツール
- Pythonによるデータ処理:以上のツールを使って、実際にデータ処理を行う方法を紹介
本連載では、その第一弾として「NumPy」と呼ばれる科学計算ライブラリを取り上げます。
Pythonについては学んだけれどまだ勉強が必要なの?
Pythonにも標準で数値計算ライブラリはありますし、多くの数値データを格納するために使えるデータ構造(リストなど)もあります。では、なぜ別にツールが必要になるのでしょうか。
簡潔なコードが書ける
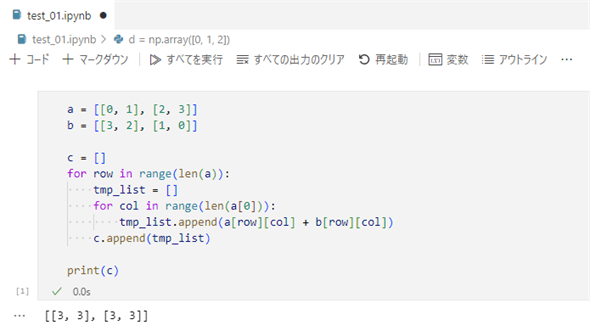
一つ例を出してみましょう。ここに以下のような2行2列(2×2)の行列が2つあり、それらの足し算をしたいとします。
上の画像を見れば分かる通り、その答えは全要素の値が3となります。では、これらの行列の和を求めるコードをPythonで書くとしたらどうなるでしょう。以下は一例です。
a = [[0, 1], [2, 3]]
b = [[3, 2], [1, 0]]
c = []
for row in range(len(a)):
tmp_list = []
for col in range(len(a[0])):
tmp_list.append(a[row][col] + b[row][col])
c.append(tmp_list)
print(c)
このコードでは、Pythonのリストを使って多次元配列に相当するデータを作ってから、二重ループを形成し、インデックスを用いて行列の各要素の足し算をしています。ハッキリいってメンドクサイですよね。念のため、実行結果を以下に示します(以下はVisual Studio Codeで実行したものです。以下、同様)。
「インデックスを使うなんてPythonぽくないよねー」という方なら次のように書くかもしれません。
a = [[0, 1], [2, 3]]
b = [[3, 2], [1, 0]]
c = []
for a_items, b_items in zip(a, b):
tmp_list = []
for a_item, b_item in zip(a_items, b_items):
tmp_list.append(a_item + b_item)
c.append(tmp_list)
print(c)
いずれにせよ、二重のループで対応する要素を取り出して加算して、それをまたリストを要素とするリストに追加していくという形に変わりはありません。
NumPyを使えば、この処理は以下のように書けます。なお、NumPyを使ったコードについてはここでは深く理解する必要はありません(numpy.array関数はNumPyが提供する配列であるndarrayオブジェクトを生成する関数であり、以下では2次元配列を作成していると考えてください)。
import numpy as np
a = np.array([[0, 1], [2, 3]]) # numpy.array関数を呼び出して多次元配列を作成
b = np.array([[3, 2], [1, 0]])
c = a + b
print(c)
強調書体で表示した「c = a + b」という部分を見てください。NumPyを使うと、ループを書いて各要素を足し算して……のようなことを全く考えないで単純に足し算をするだけで済んでしまいます。今の例は2次元(行列)でしたが、データの1次元の並びであるベクトルや、2次元以上の配列であってもこれは同じです。そして、このような記述の仕方をNumPyでは「ベクトル化(vectorization)」(ベクトル化記法)などと呼びます。
こちらも念のために実行結果を示しておきましょう。PythonのリストとNumPyのndarrayオブジェクトとで表示に差はありますが、計算結果は同一です。
実際のところは、単に記述がシンプルになるだけではありません。こうしたコードの多くは、実際にはCを使って記述/コンパイルされたコードにより実行されます。そのため、Pythonのforループで各要素の足し算を行うよりも、はるかに高速に実行できるのです。
同じことをするコードを素のPythonよりもスッキリと記述できること。配列の演算が高速に行えること。これらはNumPyを使うことの大きなメリットといえます。
面倒なことはNumPyがよろしくやってくれる
もう1つ「ブロードキャスト」という機構も紹介しておきましょう。
ブロードキャストとは「異なるサイズのndarrayを演算する際に、それらのサイズがあたかも同じであるかのように処理する」機構のことです。
といっても、分かりにくいので簡単な例を示します(先ほども使いましたが、numpy.array関数はNumPyが提供する配列を作成する関数です)。
d = np.array([0, 1, 2]) # numpy.array関数で1次元配列(ベクトル)を作成
e = d + 1
この結果はいったいどうなるでしょうか。変数cが参照しているのは、1次元配列(ベクトル)です。そして、それに整数値「1」(整数値や浮動小数点数値、複素数値をスカラーと呼ぶこともあります)を足そうとしています。Pythonのリストを使って同じことをしたら、次のように例外が発生するところですよね。
f = [0, 1, 2]
g = f + 1 # TypeError
以下を見れば、確かにPythonのリストに1を加算しようとしたらTypeError例外が発生したことが確認できます。
しかし、NumPyの配列では例外を発生することなく、コードを実行できます。その値を表示するとどうなるでしょう。
上に示したように、1次元配列のそれぞれの要素に1が加算された配列がその結果となります。もしも、コードを書いた人が「配列の各要素に1を加算したい」として、先ほどのコードを書いたのなら、これはまさにその通りの振る舞いとなっています(筆者としてはそれ以外にこのコードの意図をどう捉えればよいか分からないのですが)。しかし、本来ならそれを行うには次のようなコードを書く必要があるはずです。
d = np.array([0, 1, 2])
e = d + np.array([1, 1, 1])
つまり、全ての要素の値が1となるNumPyの配列を用意して、それを元の配列と加算するというわけです(このときには要素の総数や配列の次元数、各次元の要素数が同一である必要もあるでしょう)。しかし、このようなことをしないで、単なる整数値「1」をNumPyの配列numpy.ndarray([0, 1, 2])と同じく3要素の配列であるかのように扱ってくれることを「ブロードキャスト」と呼びます。以下に抜き出したコードを見比べればすぐに分かりますが、これもまた自分がしたいことをキレイに記述できることへとつながっています(ブロードキャストできない場合ももちろんあります)。
# ブロードキャストを使った場合
e = d + 1
# ブロードキャストを使わない場合
e = d + np.array([1, 1, 1])
つまり……
今見たような特徴を持つNumPyは多くの人からの人気を得て、現在ではPythonで数値計算を行うためのデファクトスタンダードとなっています。さらには、多くのライブラリやフレームワークでも内部でNumPyを使用したり、NumPyのデータ(配列)との相互変換が可能になっていたりしています。簡単にいえば、NumPyは他のライブラリやアプリケーションが使用する基盤となっているということです。
さらにいえば、PythonはNumPyを使うための基盤ともいえます。このようなことが積み重なって、「データ分析や科学計算、機械学習やディープラーニングをやろう→あのライブラリやこのライブラリを使いたい→使いこなすにはNumPyに関する知識が必要→Pythonについての知識も必要」という流れができ、現在ではデータ分析やAI、機械学習などの世界ではPythonとPythonで使える各種のライブラリがはやっているというわけです(もちろん、それはNumPyだけが優れていたからというわけではなく、優れたライブラリやフレームワークがおのずとPythonのエコシステム内に集合してきたからといえます)。
つまり、Pythonで数値計算を伴う何らかの処理を行おうというのであれば、NumPyについて知っておくことはとても重要だということです。これは本シリーズが対象とするデータ処理だけに当てはまることではありません。機械学習でもディープラーニングでも、扱うのは大量の数値データです(テキストだって何らかの形で数値データ化することで処理が行われます)。
NumPyについて隅の隅まで知る必要はありません(それは本フォーラムで公開している「Python入門」でも同様です)。しかし、ある程度の基礎を身に付けていれば、これから先にNumPyを使ったコードを書くときにその流儀に従った書き方ができるようになるでしょうし(例えば、上で見たベクトル化やブロードキャスト)、誰かが書いたコードを読むときにもその意味や意図をスムーズに読み取れるようになるでしょう。
NumPyとは?
というわけで、ここまでに見てきたことも含めて、NumPyが提供する機能を以下に簡単にまとめます。
- NumPyではndarrayと呼ばれる多次元配列(N-dimensional array:ndarray)オブジェクトが処理の中心となる。ndarrayオブジェクトは1次元(ベクトル)、2次元(行列、マトリクス)、3次元以上(テンソル)のさまざまな種類の配列を扱える
- ベクトル化:ndarray同士の演算を簡潔かつ高速に行えるようにする機構。ループ処理や要素ごとの演算はCで実装されたコードにより実行される
- ブロードキャスト:多次元配列同士の演算を行う際に、両者のサイズを自動的に整えてくれる機能
- ユニバーサル関数:多次元配列の各要素に対して一括して適用できる関数のこと。加減乗除や三角関数などさまざまな関数が用意されていて、プログラマーが独自に定義することも可能
- 基本的な統計関数:最大値、最小値、合計値、平均値、中央値、分散、標準偏差などを計算する関数群
なお、NumPyのndarrayには「ある配列にはある種のデータ型の値だけが格納される」という大きな特徴があります。また、一度確保した多次元配列のデータ数は変更できません。多次元配列に行や列を追加しようとすると、新たに多次元配列が新たに生成されます(NumPyの内部では高速な計算を行うためにメモリを連続して確保することから、このようになっていると考えるとよいでしょう)。
ユニバーサル関数については紹介をしていませんでしたが、これは多次元配列(ndarray)の要素一つ一つに対して何らかの処理を適用し、元の多次元配列と同じ数の多次元配列を返すものです。例えば、以下はndarrayの各要素を二乗した新しい配列を得る例です。
x = np.array([0, 1, 2])
y = np.power(x, 2)
print(y) # [0 1 4]
基本的な統計関数もNumPyには含まれています。これらを使えば、多次元配列に何らかのデータを読み込んで、それらの記述統計量を簡単に算出することも可能です(これについては後続の回で紹介しましょう)。
既に述べたように、Pythonの言語自体と標準ライブラリを使うだけでも数値計算や科学計算を行って大量のデータから何らかの知見を得ることは可能でしょう。ですが、NumPyが持つ上記の機能を活用することで、自分がしたいことを簡潔に、しかも高速に行えるようになるはずです。Pythonをある程度覚えたら、その次にNumPyを身に付けるというのはデータ分析やデータ処理をしたいという人にとっては自然な流れといえます。
そういうわけで、本連載ではNumPyを使う上で覚えておくべき基本的な知識を紹介していくことにしましょう。次回はNumPyの最重要なデータ構造である多次元配列(ndarray)について見ていくことにしましょう。
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ

 Pythonの次はNumPyを勉強してみようかな
Pythonの次はNumPyを勉強してみようかな


 作成した1次元配列の各要素に1が加算されている
作成した1次元配列の各要素に1が加算されている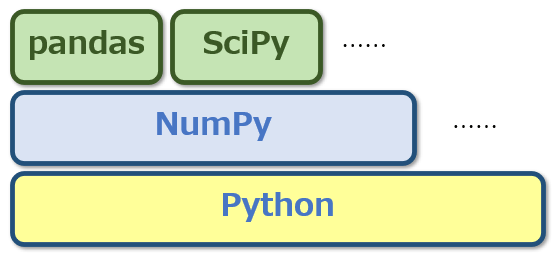 NumPyはPythonでデータ処理を行うための基盤となっている
NumPyはPythonでデータ処理を行うための基盤となっている



