[NumPy超入門]データ処理の最初の一歩! 基本統計量からデータの特徴を把握しよう:Pythonデータ処理入門(2/2 ページ)
基本統計量の確認
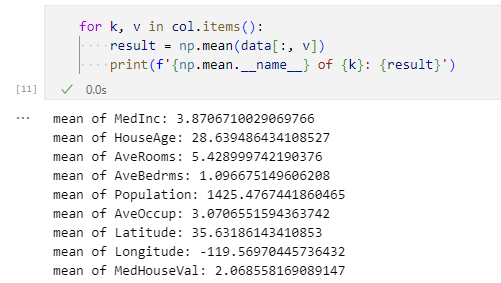
ではまずは2次元配列の各列の平均値を求めてみましょう。ここでは先頭列(所得の中央値)の平均値を見てみます。
mean_v = np.mean(data[:, col['MedInc']])
print(mean_v) # 3.8706710029069766
所得の中央値の平均が得られたのはよいのですが、単位が分からないという恐ろしい事態がやってきました。が、先ほど紹介した「California Housing」では「恐らく1万ドル(=10,000ドル)単位だと推定される」とあるので、それをそのまま採用すると、平均の所得は3.9万ドルくらいになりますね。今のカリフォルニアだとこの所得はなかなか厳しいかもしれません。
これと同じことを同様なコードで試すことも可能ですが(そのため、辞書colを作成しました)、辞書colのitemsメソッドを使ってループを回すことで簡単に各列の平均値を求められます。
for k, v in col.items():
result = np.mean(data[:, v])
print(f'{np.mean.__name__} of {k}: {result}')
itemsメソッドを使うと辞書の鍵と対応する値を反復できるので、ここでは反復されたキーを変数k、その値を変数vに代入し、それらの値を使って平均値を計算しています。注意してほしいのは「np.mean.__name__」という部分です。こう書くことでnumpy.mean関数の名前を取得できます。以下が実行結果です。
実行結果を見ると、np.mean.__name__属性が関数の名前(ここではmean)になっていることが分かります。つまり、何かの関数があったときに「関数.__name__」とすればその関数名が得られるということです。
このことを利用して、だいたい次のようなコードが書けます。
def calc(func, data, col):
for k, v in col.items():
result = func(data[:, v])
print(f'{func.__name__} of {k}: {result}')
funcs = [基本統計量を確認する関数を要素とするリスト]
for func in funcs:
calc(func, data, col)
calc関数の中身は先ほど見ていただいたコードとほぼ同様です。ただし、呼び出す関数をパラメーターに受け取るようになっているところが違います。そして、使いたい関数をリストの要素として、for文の中でcalc関数に2次元配列や辞書colと一緒に関数を渡すことで、勝手に計算してもらおうという考えです(calc関数は2つ目のfor文の中に展開してしまっても構いません)。
実際にcalc関数を定義して、今度は試しにnumpy.max関数を使って計算してみるコードを以下に示します。
def calc(func, a, col):
for k, v in col.items():
result = func(a[:, v])
print(f'{func.__name__} of {k}: {result}')
calc(np.mean, data, col)
実行結果は以下の通りです。
うまく動いているようなので、基本統計量を調べる関数を要素とするリストを作成して、for文を回してみましょう。
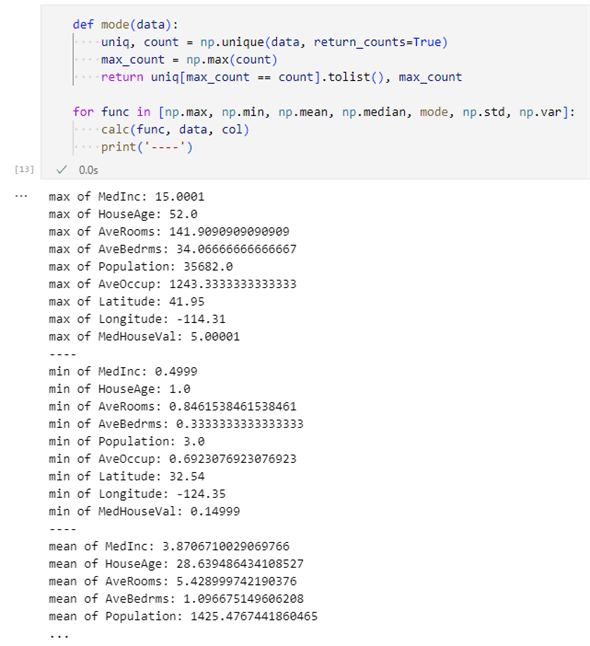
def mode(data):
uniq, count = np.unique(data, return_counts=True)
max_count = np.max(count)
return uniq[max_count == count].tolist(), max_count
for func in [np.max, np.min, np.mean, np.median, mode, np.std, np.var]:
calc(func, data, col)
print('----')
ここでは前回でも紹介した最頻値を求める関数を定義して、それを含んだ基本統計量を計算する関数をリストの要素としてfor文を回しています。実行結果は以下の通りです。
これは出力が長過ぎますね。多分、うまく実行できているのでしょうが、これだと基本統計量を確認しようという気にはなりません(がっくり)。
というわけで、急ごしらえで以下のコードを書きました(都合により最頻値を求める新しい関数mode2も定義しています。これは最頻値が複数あるとndarrayオブジェクトではなくリストが返送される点が一括処理には向いていなかったからです)。
def calc2(func, a, col):
result = [f'{func(a[:, v]).item():=10.4f}' for k, v in col.items()]
result = [f'{func.__name__:6}'] + result
result = ' | '.join(result)
return result + '\n'
def mode2(data):
uniq, idx = np.unique(data, return_counts=True)
max_count = np.max(idx)
return uniq[max_count == idx][0]
header = ' | ' + ' | '.join([f'{c:10}' for c in columns])
result = header + '\n' + '-' * 125 + '\n'
for func in [np.max, np.min, np.mean, np.median, mode2, np.std]:
result += calc2(func, data, col)
print(result)
詳しくは説明しませんが、ワチャワチャしているところは出力がキレイになるように書式を整えているコードです。本質的には先ほどのコードと同様です。また、変数headerには各列を含む文字列を代入して、やはり出力がキレイになるようにしています。
このコードを実行した結果を以下に示します(pandasのdescribeメソッド的な出力を目指してみました)。
各列について最大値、最小値、平均値、中央値、最頻値、標準偏差が見やすく出力されるようになりました。
この画像を見て、少しだけですが検討を加えてみましょう(緯度経度を見ることで地理的な側面から考察が可能かもしれませんが、ここでは省略します)。
- MedInc:平均が3.87程度、標準偏差が1.9程度であることから所得は2〜6万ドルに間に広がっていると思われる。その一方で、最大値は15.0とかなり大きな値になっている。かなりの高収入を得ている人たち(ブロックグループ)が存在するかもしれない
- HouseAge:平均で築29年、前後に12年ほどの範囲に70%ほどの建物が含まれる一方で、最大値も築52年ということで古いものから新しいものまでまんべんなく存在していると思われる
- AveRooms:5部屋前後の部屋数が一般的。だが、部屋数がかなり多いものもある(ホテル? 別荘? 筆者には想像がつきません)。かなりの高収入世帯が存在している可能性
- AveBedrms:AveRoomsと同様な傾向
- Population:ブロックグループにはおおよそ1000人前後が居住している。が、最大値を見ると、一部にかなりの人口密集地域があると思われる
- AveOccup:1世帯はおおよそ3人で構成される。が、1000人を超える世帯があるということは、集団生活を送る人たちが存在するということでしょうか(学生寮など?)。集団生活者が存在するブロックグループでは、PopulationやAveRoomsも高くなりそう
- MedHouseVal:平均値(2.07)と中央値(1.80)、標準偏差(1.15)と比べて最頻値(5.0)が大きくかけ離れている。豪邸が存在する予感!
データセットの基本統計量からはこんなことを筆者は考察しました。
とはいえ、このデータセットからはさらに情報を引き出せます。コードだけを取りあえず紹介しておきましょう。
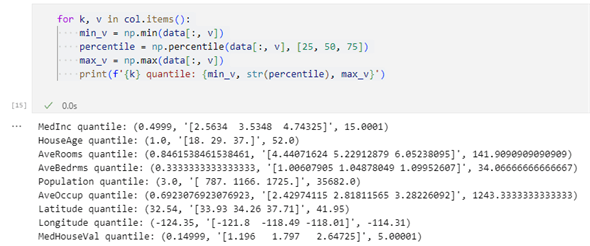
for k, v in col.items():
min_v = np.min(data[:, v])
percentile = np.percentile(data[:, v], [25, 50, 75])
max_v = np.max(data[:, v])
print(f'{k} quantile: {min_v, str(percentile), max_v}')
実行結果は以下の通りです。
これが何を意味するのかについては次回の話題とします。
Copyright© Digital Advantage Corp. All Rights Reserved.

 各列の平均値
各列の平均値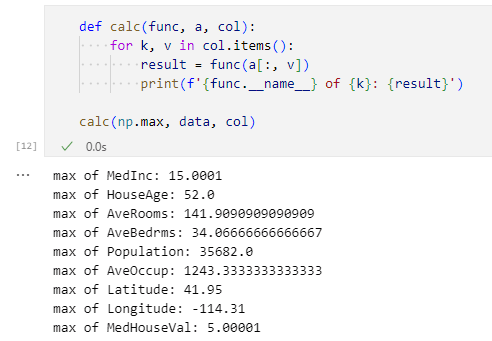 実行結果
実行結果