[NumPy超入門]箱ひげ図とヒストグラムを使ってデータセットを可視化してみよう:Pythonデータ処理入門
NumPyとMatplotlibを組み合わせ、データセットに含まれているデータがどのような分布になっているかを可視化してみましょう。新たな知見が得られるかもしれません。
連載概要
本連載はPythonについての知識を既にある程度は身に付けている方を対象として、Pythonでデータ処理を行う上で必須ともいえるNumPyやpandas、Matplotlibなどの各種ライブラリの基本的な使い方を学んでいくものです。そして、それらの使い方をある程度覚えた上で、それらを活用してデータ処理を行うための第一歩を踏み出すことを目的としています。
前回はCalifornia Housingデータセット(カリフォルニアの住宅価格のデータセット)を題材として、最大値や最小値、平均値、中央値などの基本統計量を計算し、2万行を超えるデータセットがどのような特徴を持っているのかを見てみました。今回は同じデータセットをグラフとして可視化して、さらなる特徴を探ってみることにしましょう。
CSVファイルの読み込み
前回はscikit-learnに含まれているデータセットを読み込んで、説明変数(特徴量)と目的変数(正解ラベル)を2次元配列にまとめたところで、CSVファイルとして保存していました。そこで、ここではこのデータを読み込むことにします。NumPyではCSVファイルの読み込みにはnumpy.loadtxt関数を使います。
numpy.loadtxt関数の構文を以下にまとめます(抜粋)。詳細についてはNumPyのドキュメント「numpy.loadtxt」を参照してください。
numpy.loadtxt(fname, dtype=<class 'float'>, comments='#',
delimiter=None, skiprows=0, usecols=None)
パラメーター(抜粋)には以下を指定します。
- fname:読み込むファイルの名前。指定が必須
- dtype:ファイルから読み込んだデータを基に作成する多次元配列のデータ型。デフォルト値はfloat型
- comments:コメントの始まりを表す文字の指定。デフォルト値は'#'。#で始まる行はコメント行であり、その行の内容は結果の多次元配列には含まれない。各行の最後にコメントを付加することも可能
- delimiter:読み込むファイルにおけるデータの区切り文字。デフォルト値はNoneであり、これは空白文字が区切り文字であることを意味する
- skiprows:読み込むファイルの先頭から何行を読み飛ばすかを指定。デフォルト値は0(読み飛ばさない)。上述の通り、コメント行も読み飛ばされる
- usecols:読み込む(結果の多次元配列に含める)列の指定。デフォルト値はNoneであり、これは全ての列のデータを読み込むことを意味する
前回に紹介してnumpy.savetxt関数についても同様にまとめておきます。これについても詳細はNumPyのドキュメント「numpy.savetxt」を参照してください。
numpy.savetxt(fname, X, delimiter=' ', header='')
savetxt関数のパラメーター(抜粋)には以下を指定します。
- fname:書き込み先のファイルの名前。指定が必須
- X:書き込むデータ(1次元配列または2次元配列)。指定が必須
- delimiter:データの区切り文字の指定。デフォルト値は空白文字(' ')
- header:ファイル先頭に付加するヘッダ行の内容。デフォルト値は空文字列('')
前回は「test.csv」という名前のファイルに次のようにデータを保存していました。
np.savetxt('test.csv', data, header=','.join(columns), delimiter=',')
ヘッダ行の内容は'MedInc'、'HouseAge'などの説明変数と目的変数である'MedHouseVal'をカンマ「,」で区切ったものです。ただし、先頭に'#'が付加され、全体がコメント行となっています。
前回に保存したデータを読み込むには、以下のコードを実行します。
import numpy as np
data = np.loadtxt('test.csv', delimiter=',')
あるいは先頭行の読み込みをスキップする以下のコードでも構いません(が、先頭行は上で述べたようにコメント行になっているので、skiprowsパラメーターに値を指定しなくともどのみち読み飛ばされます)。
data = np.loadtxt('test.csv', delimiter=',', skiprows=1)
いずれにせよ、numpy.loadtxt関数により、前回に保存したデータの復元ができました。次に前回と同様に'MedInc'などの文字列を介して読み込んだデータの列にアクセスできるように、読み飛ばしたヘッダ行を読み込み、辞書を作成しておきましょう。
with open('test.csv') as f:
header = f.readline()
columns = header.replace('# ', '').strip().split(',')
col = {k: v for v, k in enumerate(columns)}
print(col)
# 出力結果:
# {'MedInc': 0, 'HouseAge': 1, 'AveRooms': 2, 'AveBedrms': 3, 'Population': 4,
# 'AveOccup': 5, 'Latitude': 6, 'Longitude': 7, 'MedHouseVal': 8}
最初のwith文ではtest.csvファイルからヘッダ行を1行だけ読み込んでいます。その後のコードでは読み込んだヘッダ行から辞書を作成しています。
四分位数を求めてみる
そして、ようやく前回の最後に見ていただいたコードの登場です。
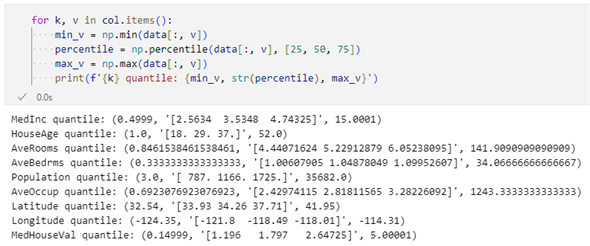
for k, v in col.items():
min_v = np.min(data[:, v])
percentile = np.percentile(data[:, v], [25, 50, 75])
max_v = np.max(data[:, v])
print(f'{k} quantile: {min_v, str(percentile), max_v}')
このコードを実行すると、以下のような出力が得られます。
このコードは各列の最小値と最大値、それから四分位数と呼ばれる値を表示するものです。四分位数とは、データの数に着目して、その4分の1、2分の1、4分の3に当たる境界がどこにあるかを求めたものです。これはデータの分布とばらつきを調べるのに役立ちます。上のコードでは列ごとに、numpy.percentile関数を呼び出していますが、これはパーセンタイルと呼ばれる値を求めるもので、これに25(%)、50(%)、75(%)をタプルにまとめたものを渡すことで四分位数を求めています。
そして、最初のMedInc(所得の中央値)の結果についていえば、データは0.4999から15.0001の範囲に分布していて、下位の4分の1に当たるデータは0.4999から2.5634に、次の4分の1に当たるデータは2.5634から3.5348に、その次の4分の1に当たるデータは3.5348から4.74325に、最上位の4分の1に当たるデータは4.74325から15.0001に分布しているというわけです。最下位と最上位を除く半数のデータが存在するのは2.5634から4.74325の間と極めて狭い範囲ですが、最大値が15.0001とかなり大きな値となっていることから所得が高くなるにつれて、その所得の幅が広くなっているといえそうです。
このようなデータの分布の仕方は、文字で表現するよりもグラフにした方が分かりやすそうですね。そこで今回はMatplotlibと呼ばれるライブラリを使って、これらを可視化してみることにしましょう。Matplotlibについては本シリーズで後日、きちんとした入門連載を行う予定なので詳しい使い方は省略しますが、これはPythonでデータを可視化するためのライブラリです。Python処理系に標準で付属するものではないので、使用するには事前に「pip install matplotlib」「py -m pip install matplotlib」などのコマンドを実行した上で、以下のコードでインポートしておく必要があります。
import matplotlib.pyplot as plt
matplotlib.pyplotモジュールには簡単にデータを可視化するための機能が含まれています。今回はその中から幾つかの関数を使ってみることにしましょう。
Matplotlibによる箱ひげ図の描画
最小値、四分位数、最大値の組を可視化するには「箱ひげ図」と呼ばれるグラフが使われます。Matplotlibではmatplotlib.pyplot.boxplot関数を呼び出すだけで、簡単にこれを行えます。以下のコードを見てください。
plt.boxplot(data[:, col['MedInc']])
plt.show()
先ほどは自分で四分位数を求めていましたが、boxplot関数には箱ひげ図を作成したいデータ(ここではMedInc列)を渡すだけです。以下がその実行結果です。
箱ひげ図は最小値と最大値に横線を描き、第1四分位数と第3四分位数の範囲を箱で囲んで、中央値はその箱の中に横線で描くことがよくあります(箱から上下に伸びた部分が「ひげ」になります)。例えば、HouseAge列を例に箱ひげ図を描くと次のようになります。
HouseAge列では各値は次のようになっていました。
- 最小値:1.0
- 第1四分位数:18
- 中央値:29
- 第3四分位数:37
- 最大値:52
図と比べるとだいたいその辺りに横線や箱、それらをつなぐひげが描かれていることが分かります。しかし、先ほどのMedInc列の箱ひげ図はこれとはちょっと異なっています。MedInc列については各値は次の通りでした。
- 最小値:0.4999
- 第1四分位数:2.5634
- 中央値:3.5348
- 第3四分位数:4.74325
- 最大値:15.0001
このことから考えると最大値の横線は図の一番上の辺りにありそうなものですが、実際には8を少し超えた辺りに横線が引かれ、その上には何やらデータがたくさん存在しているように見えます。
箱ひげ図を描くときには、ひげの上限と下限をそのまま最大値と最小値にはせずに、「第3四分位数−第1四分位数」の値を1.5倍した値を第3四分位数に加算、あるいは第1四分位数から減算したものを上限と下限にすることもあります(第3四分位数−第1四分位数の値を「四分位範囲」と呼ぶこともあります)。MedInc列はそのような形で描かれた箱ひげ図です。MedInc列では「第3四分位数−第1四分位数」はおおよそ「2.18」です。これを1.5倍した値(3.27)を、第1四分位数から減算、第3四分位数に加算したものを以下に示します。
- 下限:2.5634−3.27=−0.706(最小値は0.4999)
- 第1四分位数:2.5634
- 中央値:3.5348
- 第3四分位数:4.74325
- 上限:4.74325+3.27=8.01(最大値は15.0001)
これらの値とMedInc列の箱ひげ図を見比べると下限は実際の最小値よりも小さくなっているのでそのまま最小値の部分に横線を引き、上限は最大値まで届かないので上限の辺りで横線を引いたものとなっていることが分かります。
上限や下限から外れた値は「外れ値」(何らかの原因で他のデータとは大きく異なる値となったデータ)として扱われることもよくありますが、この例でそうした扱いをするのが適切かどうかは微妙なところです。そうしたデータが多過ぎるからです。これは高所得者層のデータが、計算された上限を超えて緩やかに分布していると考えた方がよいかもしれません。
次にこの考えが合っているかどうかを、ヒストグラムを使って見てみましょう。なお、以下のコードを実行すると、読み込んだデータの全ての列について、箱ひげ図を作成し、1つのグラフの中に表示できます。興味のある方は試してみてください。
fig = plt.figure()
fig, axes = plt.subplots(nrows=3, ncols=3, sharex=False)
for k, v in col.items():
r = v // 3
c = v % 3
axes[r, c].boxplot(data[:, v])
axes[r, c].set_title(k, fontsize=8)
plt.show()
Matplotlibによるヒストグラムの描画
ヒストグラムもまたデータの分布の仕方を調べるためのツールです。こちらはデータセットを幾つかの範囲に分割して、その範囲に含まれるデータが何個あるかを調べます(できたものを度数分布表といいます)。ここでもMedInc列を例に取りますが、イメージとしては所得がこの範囲の人が何人、その範囲の人が何人といったことを調べるということです。
度数の分布を求めるにはNumPyのnumpy.histogram関数を使い、得られた結果をmatplotlib.pyplot.bar関数でグラフにするというのが大ざっぱな手順になります。
まずnumpy.histogram関数から見ていきましょう。
numpy.histogram(a, bins=10)
他にもパラメーターはありますが、ここでは2つだけパラメーターを指定しましょう。
- a:入力するデータ
- bins:データ範囲を何個の領域に分割するかの指定。デフォルト値は10
入力するデータとビン(データセットを分割した個々の区間)の数を指定して、この関数を呼び出すと、ヒストグラム(各ビンに含まれるデータの数)、それからビンとビンの境界となる値を含んだ配列が返されます。
hist, bins = np.histogram(data[:, col['MedInc']], bins=20)
この例ではデータセットに含まれる値の範囲(最小値である0.4999から最大値である15.0001)を20個のビンに分割して、それぞれのビンに含まれるデータの数およびビンとビンの境界となる値を得るものです。
以下は、このコードを実行して、histとbinsの2つの変数に返された値を表示したところです。
変数histの値を見る限り、所得が低い方から中くらいにかけてはかなりのボリュームがありますが、高所得者層についてもそれなりの数がいることが確かに分かります。先の箱ひげ図における検討でこれらを外れ値とすべきではないかもしれないという考えはある程度正しいといえるでしょう。
その下の変数binsの値は各ビンの最小値と最大値を表す境界だと考えられます。つまり、最初のビンは0.4999から1.22491までの範囲に含まれるデータの数を表しているということです(そのため、binsの要素数はhistの要素数よりも1個多くなっています)。
後はこれをグラフとして描画するだけです。先ほどもいったように、これにはmatplotlib.pyplot.bar関数を使います。
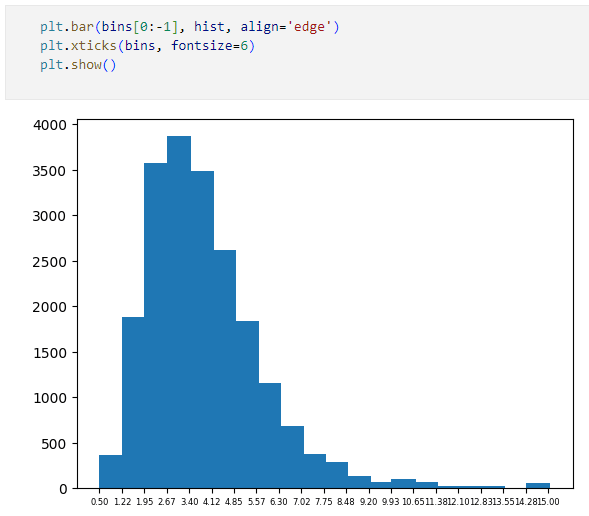
plt.bar(bins[0:-1], hist, align='edge')
plt.xticks(bins, fontsize=6)
plt.show()
bar関数の第1引数はX軸の座標を指定します。ここでは単にhistogram関数が返してきた境界値を含む配列から最後の1つを取り除いたものにしました。第2引数にはY軸の値、つまり、各ビンのデータ数を指定します。上のコードではalignパラメーターに'edge'を渡していますが、これによりグラフがX軸の目盛りに対して左寄せされます。
そのX軸の目盛りを設定しているのが次の行です。ここではX軸に最小値から最大値までが表示されるように、histogram関数が返してきた境界値を渡しています。また、フォントサイズを小さめにして、全ての値がなるべく表示できるようにしました。
以下が実行結果です。
どうでしょう。数字の羅列を見ているだけよりも、所得者層の構成がよりハッキリと把握できるのではないでしょうか。高所得者が緩やかに分布しているだろうという推測もあながち間違いではなさそうです。
こうした傾向は、基本統計量からもある程度は推測できるかもしれません。例えば、MedInc列に関しては、前回の最後に次のように検討しています。
- MedInc:平均が3.87程度、標準偏差が1.9程度であることから所得は2〜6万ドルの間に広がっていると思われる。その一方で、最大値は15.0とかなり大きな値になっている。かなりの高収入を得ている人たち(ブロックグループ)が存在するかもしれない
この検討とグラフとを見比べてみると、まあまあそれなりのデキだったと筆者的には感じてしまいます(甘いですかね)。
基本統計量だけでもそれなりの検討ができる一方で、今回紹介した箱ひげ図やヒストグラムを使って検討を加えることで、手元にあるデータセットに対する理解が一段と深まるはずです(初見での印象が可視化によって補強されるかもしれませんし、逆に印象がまるっとひっくり返ることになるかもしれません)。
このようにさまざまなツールを用いてデータセットを取り扱うことで、あまりに膨大で個々のデータを検討できない(検討してもあまり意味がない)データセットからもその特徴が見えてきます。
というわけで、今回は箱ひげ図とヒストグラムについて見てみました。次回はこのような可視化についてもう少し見てみるか、また別のお話にするか、悩んでいるところです。
Copyright© Digital Advantage Corp. All Rights Reserved.

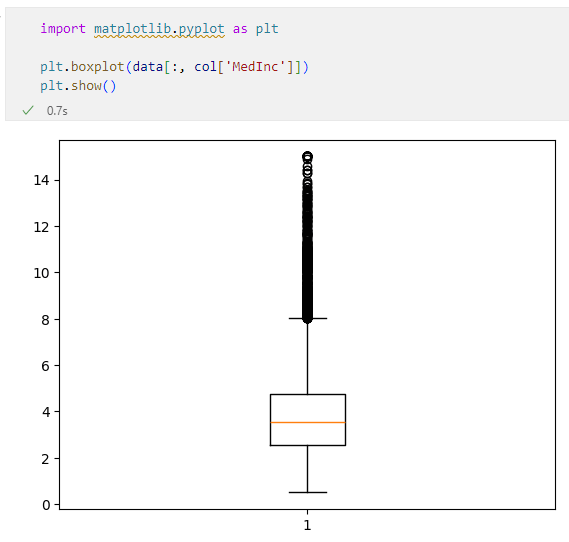 作成された箱ひげ図
作成された箱ひげ図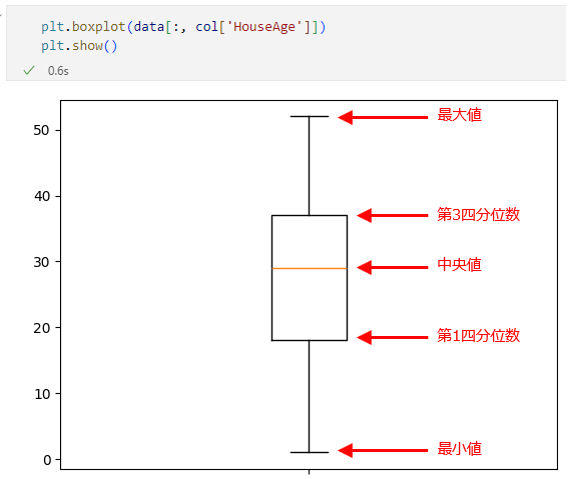 HouseAge列の箱ひげ図
HouseAge列の箱ひげ図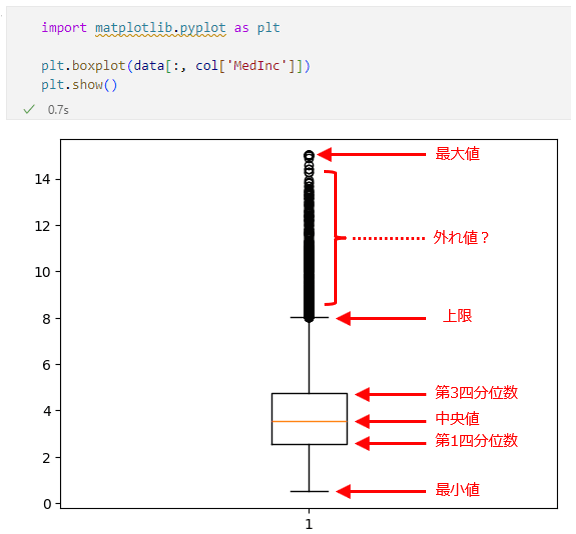 下限、上限を考慮した箱ひげ図
下限、上限を考慮した箱ひげ図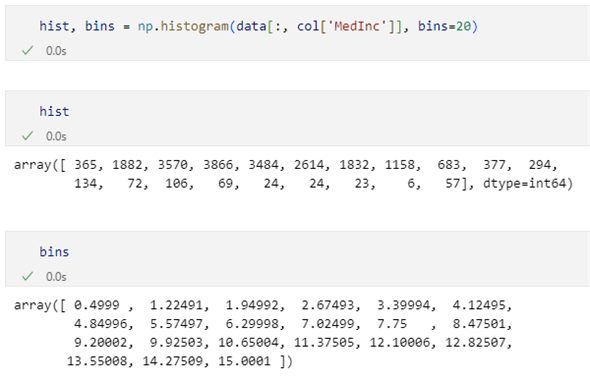
 実行結果
実行結果



