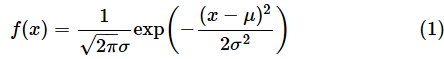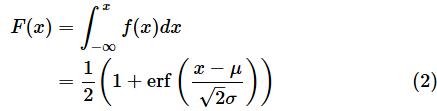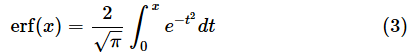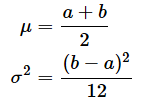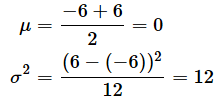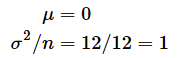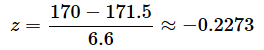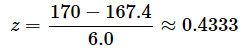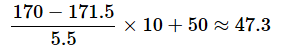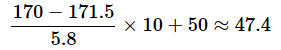［データ分析］正規分布 〜 私より背の高い人はどれぐらいいるの？：やさしい確率分布

データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載（確率分布編）の第6回。正規分布は平均値を「山」の中心として、標準偏差によって左右対称に「すそ」が広がるような形の連続型確率分布です。正規分布がどのようなものかを確認した後、確率密度関数や累積分布関数の求め方や可視化の方法を解説し、利用例などを紹介していきます。

[羽山博，著]

連載目次

連載：

『社会人1年生から学ぶ、やさしい確率分布』

　この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』連載（記述統計と回帰分析編）の続編で、確率分布に焦点を当てています。
　この確率分布編では、推測統計の基礎となるさまざまな確率分布の特徴や応用例を説明します。身近に使える表計算ソフト（Microsoft ExcelやGoogleスプレッドシート）を使いながら具体的に事例を見ていきます。
　必要に応じて、Pythonのプログラムや統計ソフト「R」などでの作成例にも触れることにします。
　数学などの前提知識は特に問いません。中学・高校の教科書レベルの数式が登場するかもしれませんが、必要に応じて説明を付け加えるのでご心配なく。肩の力を抜いてぜひとも気楽に読み進めてください。

羽山博

筆者紹介： IT系ライターの傍ら、非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。趣味の献血は心拍数が基準を超えてしまい99回で中断。心肺機能を高めるために水泳を始めるも、一向に上達せず。また、リターンライダーとして何十年ぶりかに大型バイクにまたがるも、やはり体力不足を痛感。足腰を鍛えるために最近は四股を踏む日々。超安全運転なので、原付やチャリに抜かされることもしばしば（すり抜けキケン、制限速度守ってね！）。

　データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の確率分布編、第6回です。前回は、離散型確率分布のまとめとして、さまざまな離散型確率分布の逆関数とその利用例を取り上げました。今回から連続型確率分布のお話に入ります。まずは、連続型確率分布の代表とも言われる正規分布について、その特徴や意味、確率密度関数／累積分布関数の求め方、利用例などを見ていきます。

正規分布で自分の位置を知るには

　厚生労働省による国民健康・栄養調査（2019）によると、20歳以上の日本人男性（サンプルサイズ：1968人）の平均身長は167.7cm、標準偏差は6.9でした。身長の分布が正規分布（あとで詳しく見ます）に従っているものと仮定すると（2024/08/30追記：本来は、母集団が正規分布に従っているかどうかを確認する必要がありますが、仮にそうだとすると）、この集団の中で170cmの人はどのあたりの位置にいると考えられるでしょうか（図1）。

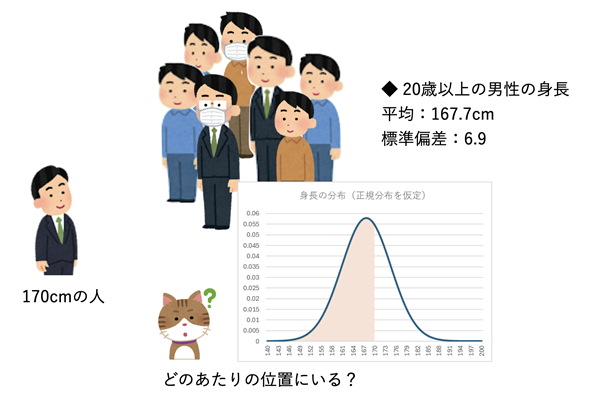図1　身長170cmの人は全体のどのあたりの位置にいるのか
平均167.7、標準偏差6.9の正規分布で、170という値は全体のどのあたりだろうか。平均よりも大きいことは分かるが、数値で何％と表すならいくらになるだろう。

　答えから先に言うと、下位から63.1％（上位から36.9％）の位置です。が、その値を求めるためには正規分布についての理解を深めておく必要があります。というわけで、今回は正規分布について丁寧に見ていきましょう（求め方だけを先に知りたい方はこちらへ）。まずは、離散と連続のおさらいからです。

　当然のことながら、身長が高いから偉いというわけではありません。「上位」「下位」は単に値の大小を表しているだけで、価値判断とは全く関係ありません。

「離散」と「連続」のおさらいから 〜 「とびとび」か「スキマがない」か

　正規分布は連続型確率分布の代表的な分布です。確率分布の意味や離散と連続の違いについては、この連載の第1回で解説しました。簡単におさらいしておきましょう。

　まず、確率変数からです。確率変数とはある事象に対して割り当てた値のことで、通常大文字のXで表します（これまでは特に明示していませんでしたが）。離散型確率分布では、確率変数Xの値としてkという変数名を使うのが一般的です。つまり、Xは確率変数そのものを一般的に表し、kは確率変数の具体的な値を表す変数だというわけです。

　離散型確率分布では、確率変数がとびとびの値を取ります。例えば、図2のようなサイコロのそれぞれの目が出る確率は離散型一様分布となり、確率変数Xは1, 2, 3, 4, 5, 6のいずれかの値を取ります。1.5などという目が出ることはありませんね。

　さらにおさらいです。ベルヌーイ分布の確率変数Xは0か1の値を取ります。例えば、サイコロで1の目が出る場合をX＝1とし、1以外の目が出る場合をX＝0とします。また、二項分布では確率変数Xが0、1、2、……、nという値を取ります。例えば、サイコロをn回投げて、1の出る回数がXに当たります。

　一方、連続型確率分布では、確率変数Xは範囲内のどの値でも取れます。連続型確率分布では、確率変数Xの具体的な値を表す変数名として小文字のxを使うのが一般的です。

　連続型確率分布の確率変数の例としては、気温や身長などがあります。例えば、気温は下限から上限までのどの値でも取れます。温度計には目盛りが付いていますが、それはあくまでも目安です。目盛りの間はいくらでも細かく（スキマなく）分けられますね。

図2　離散と連続のイメージ
離散とは値がとびとびになっていること。連続とは範囲内のどの値でも取ることができるということ。温度計には目盛りが付いているが、それはあくまでも目安であることに注意。

　では、ちょっとした問題です。デジタル体温計で測定した場合の体温は離散値でしょうか、連続値でしょうか。デジタル体温計での測定値は36.5℃のように0.1℃刻みになっていて、その間の値（36.51...℃など）は表示されないので、離散値と思われるかもしれません。しかし、それはあくまでも体温計の精度（有効数字）の問題です。体温は連続値として分析するのが適切です。

　日常の感覚では、1、2、3……という値は連続しているものと捉えられますが、英語では、このような連番は、何らかのモノが順に並んだという意味合いのserialという単語を使って、serial numberと呼びます。それに対して、上で見た「連続」を表す単語は、切れ目なく続くといった語感のcontinuousです。どちらにも「連続」という訳語を当てるので、日本語だと紛らわしいですね。また、整数だから離散、小数だから連続という意味ではないということについても注意しましょう。

正規分布ってどんな感じの分布？ 〜 確率密度関数を可視化してみよう

　身長や試験の成績などは、母集団が正規分布に従っているものと仮定して分析を行うことがよくあります。正規分布は平均μと標準偏差σで決まる分布です。分布を一意に決めるこれらの値を母数（パラメーター）と呼ぶ、ということはこの連載の第1回で説明しましたね。

　正規分布の確率密度関数を可視化すると、図3のようになります。このことについてはすでにご存じの方も多いでしょう。平均のところが一番高くなっていて、左右対称に裾野が広がるような形です。なんとなくですが、成績の分布のように見えますね。

　いやいや、それ以前に「確率密度関数って何？」という方も多いと思いますが、理屈は後回しにして、図3のグラフを先に作成してみましょう。手順は図の後に記してあります。正規分布の確率密度関数の値はNORM.DIST関数で求められます。引数には、確率変数の値と、母数（平均と標準偏差）を指定します。ここでは、平均μ＝60、標準偏差σ＝10とします。

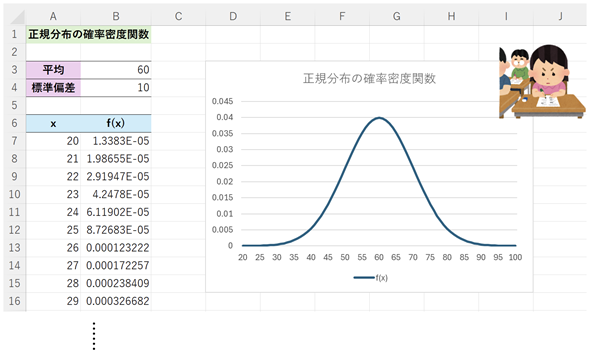図3　正規分布の確率密度関数の例
正規分布（平均μ＝60、標準偏差σ＝10）の確率密度関数。ここでは、x＝20〜100について可視化した。平均値のところが一番高い山になっており、左右対称に裾野が広がるグラフになる。

　グラフ作成の手順は以下の通りです。サンプルファイルをこちらからダウンロードし、［正規分布］ワークシートを開いて試してみてください。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから［ファイル］−［コピーを作成］を選択し、Googleドライブにコピーしてお使いください。具体的な操作方法は、サンプルファイル内に記載しています。

◆ Excelでの操作方法（タイトルや軸の書式などの細かい設定は省略）

• セルB7に=NORM.DIST(A7:A87,B3,B4,FALSE)と入力する
  • 古いバージョンのExcelでスピル機能が使えない場合は、結果が求められるセル範囲（セルB7〜B87）をあらかじめ選択しておき、関数を入力した後、入力の終了時に［Ctrl］＋［Shift］＋［Enter］キーを押す
• セルB6〜B87を選択する
• ［挿入］タブを開き、［折れ線／面グラフの挿入］ボタンをクリックして［折れ線］を選択する
• ［グラフのデザイン］タブを開き、［データの選択］ボタンをクリックする
• ［データソースの選択］ダイアログボックスで［横（項目）軸ラベル］の下の［編集］ボタンをクリックする
• ［軸ラベル］ダイアログボックスで［軸ラベルの範囲］ボックスをクリックし、セルA7〜A87を選択する
• ［OK］をクリックして［軸ラベル］ダイアログボックスを閉じる
• ［OK］をクリックして［データソースの選択］ダイアログボックスを閉じる

　正規分布の確率密度関数f(x)は以下の式で定義されますが、NORM.DIST関数で求められるので、この式を無理に暗記する必要はありません。

　exp(x)は自然対数の底e＝2.71828...のx乗を表します。なお、文献によっては、

の部分が

と表記されている場合もあります。

　NORM.DIST関数の引数は以下のように指定します。

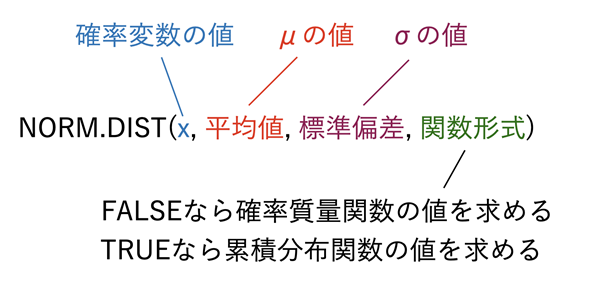図4　NORM.DIST関数に指定する引数
図3の例では、関数形式としてFALSEを指定し、確率変数の値としてA7:A87というセル範囲を指定しているので、スピル機能によりセルA7〜A87の値に対する確率密度関数の値が求められる。関数形式にTRUEを指定すれば累積分布関数の値が求められる。

連続型確率分布や正規分布についての留意点

　以下に、 連続型確率分布や正規分布についての留意点を箇条書きにしておきます。

• 離散型確率分布でのf(k)は確率質量関数（probability mass function）と呼ぶが、連続型確率分布でのf(x)は確率密度関数（probability density function）と呼ぶ
• f(x)の値は、確率変数の値がxのときの確率ではない。この値は累積分布関数の微分係数と考えられる（後述）
• グラフとx軸とで囲まれた範囲の面積は1である
• 正規分布では、台（xの取り得る値の範囲）は−∞〜∞

　特に、確率密度関数f(x)の値は、確率変数の値がxのときの確率ではないことに注意してください。図3の例で具体的に言うと、x＝60のとき、f(x)の値は0.03989ですが、この値はx＝60である確率ではないということです。連続型確率分布では、確率変数の特定の値に対する確率を求めることはできません。しかし、累積分布関数（後述します）によって、一定の範囲（例えば、x＝40〜60）に対する累積確率を求めることはできます。累積分布関数の値は、確率変数の値がある範囲に入る確率です。

　じゃあ、f(x)の値っていったい何、と思われる方も多いでしょう。上の箇条書きでは「累積分布関数の微分係数」と記していますが、日常の言葉で言えば、例えば、「x＝60でどの程度、累積確率が増えるか」という度合い（傾向）を表すもの、といった答えになります。

そもそも正規分布って何？ 〜 二項分布と正規分布の関係

　前回までの離散型確率分布では、サイコロを振ったり、ガラガラを回したり、野球選手のヒットの出る確率を使ったり……と、具体的な例を基に確率質量関数がどのような式で表されるのかを見てきました。しかし、今回の正規分布では、実世界での事例を基に確率密度関数を表す（1）式をどう導き出するのかよく分かりませんね。

　実は、離散型確率分布の代表格とも言える二項分布と、連続型確率分布の代表格とも言える正規分布には極めて深い関係があります。二項分布のpを変えずにnをどんどん増やしていくと、平均np、分散np(p−1)の正規分布に近づくことが分かっています。

　ちなみに、二項分布のnpを変えずにnをどんどん増やしていくと（その場合、pがどんどん小さくなる）、ポアソン分布になります。この連載の第4回で取り上げました。

　式の導出は高校の数学でもできますが、かなり大変なので割愛します。その代わり、Excelを使って具体的な例でその様子を可視化してみましょう。図5は二項分布のnを大きくした確率質量関数のグラフ（棒グラフ）と、正規分布（平均np、分散np(p−1)）のグラフ（折れ線グラフ）を重ねてみた例です。n＝20ぐらいでもほぼ重なっていることが分かります。

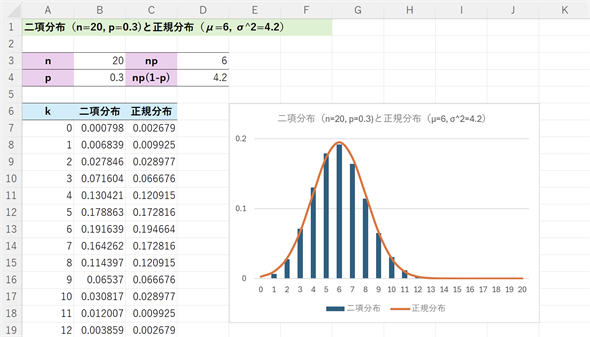図5　二項分布と正規分布の関係
n＝20は20回の打数を、p＝0.3は3割打者を表すと考えればよい。20回の打数のうちヒットが出る回数とその確率は二項分布で求められる（棒グラフの部分）。μ＝6, σ＝4.2の正規分布のグラフ（折れ線グラフ）を描いてみると、それらがほぼ重なることが分かる。

　図4のグラフを作成する方法については、サンプルファイルの［二項分布と正規分布］ワークシート中に掲載しています。ここでは、各セルに入力されている数式のみを記しておきます。

• セルD3： =B3*B4　…… μ＝npの値
• セルD4： =D3*(1-B4)　…… σ²＝np(1−p)の値
• セルB7： =BINOM.DIST(A7:A27,B3,B4,FALSE)　…… 二項分布の確率質量関数の値
• セルC7： =NORM.DIST(A7:A27,D3,SQRT(D4),FALSE)　…… 正規分布の確率密度関数の値

　正規分布の平均μはnp＝20×0.3＝6とし、分散σ²はnp(1−p)＝6×(1−0.3)＝4.2としています。NORM.DIST関数には分散ではなく標準偏差を指定するので、3番目の引数がSQRT(D4)となっていることに注意してください。

正規分布の累積分布関数を可視化してみよう

　すでに述べたように、連続型確率分布では、確率変数の特定の値に対する確率を求めることはできません。しかし、累積分布関数によって、一定の範囲に入る確率（累積確率）を求めることはできます。累積分布関数は基本的には離散型確率分布の場合と同じ考え方で、確率変数Xの値がxとなるまでの累積確率を関数として表したものです。累積分布関数がどのようなものであるか、図6で確認しておきましょう。グラフの作成手順は図の後に記してあります。

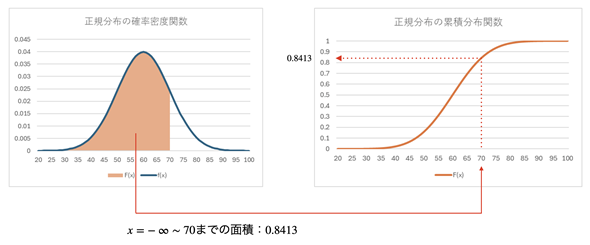図6　正規分布の確率密度関数f(x)と累積分布関数F(x)
正規分布の台はx＝−∞ 〜∞だが、x軸を−∞〜∞にすることはできないので、目盛りを20〜100までとした。左側の確率密度関数のグラフでは、累積確率はグラフとx軸で囲まれた部分の面積で表される。例えば、x＝70までの累積確率はオレンジ色で塗りつぶした部分の面積（＝0.8413）となる。右側の累積分布関数のグラフはxに対する累積確率をプロットしたもの。例えば、x＝70に対するF(x)の値は0.8413になる。

　図6の左側は正規分布の確率密度関数です。x軸とグラフで囲まれた面積が累積確率に当たります。例えば、x＝−∞ 〜70までの累積確率はオレンジ色で塗りつぶされた部分の面積（＝0.8413）になります。一方、xに対する累積確率（面積）をプロットしていったものが累積分布関数です。こちらは右側のようなグラフになります。右側のグラフでは、x＝70に対するF(x)の値が0.8413になります。

　高校数学の記憶がある方は、図6を見て、累積分布関数F(x)は確率密度関数f(x)を積分したものだと気付くと思います。数式で表すと以下のようになります。

　ただし、erfは誤差関数と呼ばれる以下の関数です。

　Excelでは、正規分布の累積分布関数の値もNORM.DIST関数で求められるので、上の（2）式や（3）式を無理に覚える必要はありません（ちなみに、誤差関数の値もERF.PRECISE関数で求められますが、これ以上は触れないことにします）。

　グラフ作成の手順は以下の通りです。サンプルファイルの［確率密度関数と累積分布関数］ワークシートを開いて試してみてください。Googleスプレッドシートでは、サンプルファイル内に手順を記載しています。

◆ Excelでの操作方法（タイトルや軸の書式などの細かい設定は省略）

• 確率密度関数のグラフ作成
  • セルB7に=NORM.DIST(A7:A87,B3,B4,FALSE)と入力する
    • 古いバージョンのExcelでスピル機能が使えない場合は、結果が求められるセル範囲（セルB7〜B87）をあらかじめ選択しておき、関数を入力した後、入力の終了時に［Ctrl］＋［Shift］＋［Enter］キーを押す
  • セルB6〜B87を選択する
  • ［挿入］タブを開き、［折れ線／面グラフの挿入］ボタンをクリックして［折れ線］を選択する
  • ［グラフのデザイン］タブを開き、［データの選択］ボタンをクリックする
  • ［データソースの選択］ダイアログボックスで［横（項目）軸ラベル］の下の［編集］ボタンをクリックする
  • ［軸ラベル］ダイアログボックスで［軸ラベルの範囲］ボックスをクリックし、セルA7〜A87を選択する
  • ［OK］をクリックして［軸ラベル］ダイアログボックスを閉じる
  • ［OK］をクリックして［データソースの選択］ダイアログボックスを閉じる

• 累積確率の塗りつぶし
  • ［グラフのデザイン］で［データの選択］ボタンをクリックする
  • ［データソースの選択］ダイアログボックスで［凡例項目（系列）］の下の［追加］ボタンをクリックする
  • ［系列の編集］ダイアログボックスで［系列名］ボックスをクリックし、セルB6を選択する
  • ［系列の編集］ダイアログボックスで［系列値］ボックスをクリックし、すでに入力されている{=1}を削除してから、セルB7〜B57を選択する
  • ［OK］をクリックして［系列の編集］ダイアログボックスを閉じる
  • ［OK］をクリックして［データソースの選択］ダイアログボックスを閉じる
  • ［グラフのデザイン］で［グラフの種類の変更］ボタンをクリックする
  • ［グラフの種類の変更］ダイアログボックスで、左のリストから［組み合わせ］を選択する
  • ［系列名］に「f(x)」と表示されている行の［グラフの種類］リストから［折れ線］を選択する
  • ［系列名］に「F(x)」と表示されている行の［グラフの種類］リストから［面］を選択する
  • ［OK］をクリックして［グラフの種類の変更］ダイアログボックスを閉じる

• 累積分布関数のグラフ作成
  • セルC7に=NORM.DIST(A7:A87,B3,B4,TRUE)と入力する
    • 古いバージョンのExcelでスピル機能が使えない場合は、結果が求められるセル範囲（セルC7〜C87）をあらかじめ選択しておき、関数を入力した後、入力の終了時に［Ctrl］＋［Shift］＋［Enter］キーを押す
  • セルC6〜C87を選択する
  • ［挿入］タブを開き、［折れ線／面グラフの挿入］ボタンをクリックして［折れ線］を選択する
  • ［グラフのデザイン］タブを開き、［データの選択］ボタンをクリックする
  • ［データソースの選択］ダイアログボックスで［横（項目）軸ラベル］の下の［編集］ボタンをクリックする
  • ［軸ラベル］ダイアログボックスで［軸ラベルの範囲］ボックスをクリックし、セルA7〜A87を選択する
  • ［OK］をクリックして［軸ラベル］ダイアログボックスを閉じる
  • ［OK］をクリックして［データソースの選択］ダイアログボックスを閉じる

　ずいぶん遅くなりましたが、冒頭の問題に対する答えの求め方を見ておきましょう。平均167.7、標準偏差6.9の正規分布で、170という値が全体のどの位置に当たるかは累積分布関数で求められます。具体的には=NORM.DIST(170, 167.7, 6.9, TRUE)で求められます。空いているセルに関数を入力して確認してみてください（サンプルファイルの完成例ではセルE32に入力されています）。0.6305...という値が表示されるはずです。下位から63.1％の位置であるということですね。

正規分布はどんなところに現れるのか？ 〜 中心極限定理とは

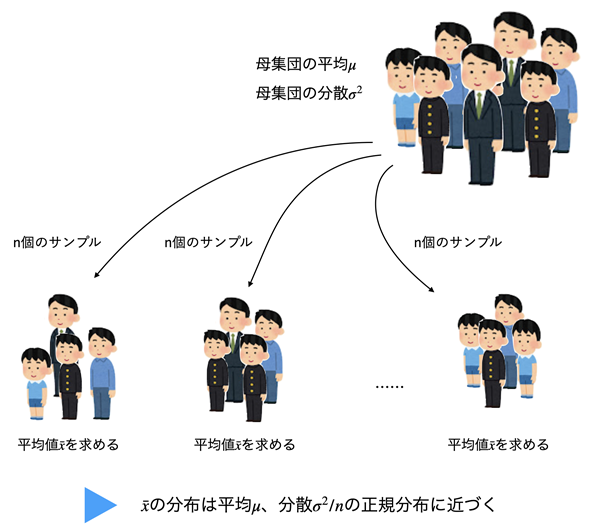
　二項分布の試行を数多く行うと、正規分布に近づくことはすでにお話ししました。正規分布を日常の感覚と直接結び付けて考えるのは難しいですが、その延長線上にあることは理解できたと思います（今回のお話がちょっと理屈っぽくなったのもそのためですね）。そこで、正規分布がどんなところに現れるのかを見ておきましょう。中心極限定理と呼ばれる重要な定理についてお話しします。

　中心極限定理とは、母集団の分布がどのような分布であっても、そこからサンプルを何度も取り出すと、それらの平均値

が正規分布に近づくという定理です。具体的には母集団の平均をμ、分散をσ²としたとき、n個のサンプルを何度も取り出すと、

は平均μ、分散σ²/nの正規分布に近づくということです。

図7　中心極限定理のイメージ

　中心極限定理についても証明はかなり難しくなるので、例で見てみましょう。母集団の分布は何でもいいので、ここではa ≤ x ≤ bの連続型一様分布を使って試します。連続型一様分布の平均μと分散σ²は以下の通りです。

　そこで、a＝−6, b＝6の一様分布を考えます。ここからn＝12個のサンプルを10000回取り出して、それぞれの平均値を求め、ヒストグラムを作ってみましょう。この場合、

なので、中心極限定理によって、平均と分散がそれぞれ、

の正規分布になるはずです。

　このシミュレーションはExcelを使ってもできますが、多数のセルを使う必要があり（地道にやるなら12×10000個以上）、かなり面倒です。一応、サンプルファイルに作成例は含めてあります（［中心極限定理］ワークシート）が、ここでは、Pythonのプログラムを使うことにします（リスト1）。

　サンプルプログラムはこちらから参照できます。リンクをクリックすれば、ブラウザが起動し、Google Colaboratoryの画面が表示されます（Googleアカウントでのログインが必要です）。コードセルをクリックし、［Shift］+［Enter］キーを押してコードを実行してみてください。結果は図8のようになります。コードの詳細については解説しませんが、コメントとリスト1の説明を見れば何をやっているかが大体分かると思います。

import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt

# 12個の一様乱数を10000回作る（10000行×12列）
sample = np.random.rand(10000, 12) * 12 - 6  # 0〜1の乱数なので、12倍して6を引けば-6〜6の範囲になる
# 各行の平均値を求める
means = sample.mean(axis=1)
# ヒストグラムを作成する（範囲は-4〜4まで、階級は100個、縦軸を確率とする）
plt.hist(means, range=(-4, 4), bins=100, density=True)

# 標準正規分布
x = np.linspace(-4, 4, 100)  # -4〜4までを100個に分けた数列を作る
y = norm.pdf(x, loc=0, scale=1)  # 標準正規分布の確率密度関数の値を求める
plt.plot(x, y) # グラフを作る

# グラフを表示する
plt.show()

リスト1　中心極限定理のシミュレーションを行う
NumPyのrandom.rand関数に、行数と列数を指定すれば、一様乱数の配列が作成できる。後は、meanメソッドを使って各行の平均値を求め、matplotlib.pyplotモジュールのhist関数を使ってヒストグラムを作成するだけ。density=Trueは「縦軸を確率にする」という指定。さらに、scipy.statsモジュールのnorm.pdf関数を使い、平均loc=0、標準偏差scale=1の正規分布の確率密度関数の値を求め、グラフを重ねて描く。実行例は図8を参照。

　なお、平均が0、標準偏差が1（分散も1となる）の正規分布を標準正規分布と呼びます。a＝−6, b＝6, n＝12としたのはシミュレーションの結果が標準正規分布に近くなるようにするためです。

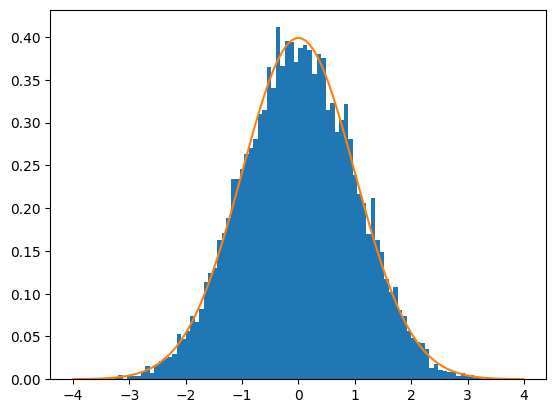図8　n個のサンプルの何度も取り出して求めた平均値のヒストグラムと標準正規分布のグラフ
棒グラフは、−6〜6までの一様乱数から12個のサンプルを10000回取り出して、それらの平均値を基に作成したヒストグラム。折れ線グラフは平均0、標準偏差1の標準正規分布。ほとんど重なっていることが分かる。

　一様乱数は毎回異なる値が作成されるので、図8のヒストグラムも毎回異なる形になりますが、標準正規分布とほぼ重なります。実は、二項分布のnを大きくしていくと正規分布に近づくというのも中心極限定理によるものです。

　母集団が正規分布であると仮定されない場合でも、平均値などの分析のために広く正規分布が使われるのは、この中心極限定理を根拠としています。なお、このように、前提を多少満たさないとしても、妥当な結果が得られることを頑健性（robustness）があると言います。

　標準正規分布の確率密度関数と累積分布関数の値をExcelで求めるには、NORM.DIST関数を使って、平均値に0を、標準偏差に1を指定してもいいのですが、NORM.S.DIST関数も利用できます。NORM.S.DIST関数を使えば、標準正規分布であることが明確に分かりますし、引数の指定も簡単になります。関数の形式については、この記事の最後をご参照ください。

異なる集団の間で値の大小を比較するには 〜 標準化の方法と偏差値の求め方

　冒頭で示した身長のお話ですが、国民健康・栄養調査（2019）には、年齢層による平均値と標準偏差も掲載されています。それによると、20歳代の男性は身長の平均が171.5cm、標準偏差が6.6です。一方、60歳代の男性は身長の平均が167.4cm、標準偏差が6.0です。では、これらの集団の中で、身長170cmの20代男性と、身長170cmの60代男性ではどちらの方が背が高いでしょう？

　同じ値なので身長は同じというのはもっともな答えです。しかし、「集団の中で」という条件が入っていると話は変わります。20歳代の平均身長は171.5cmで、60歳代の平均身長は167.4cmなので、集団の中で考えると、20歳代の170cmは低い方で、60歳代の170cmは高い方だろうとも考えられます。このように、平均値や標準偏差が異なる集団の間で、どの位置にいるかを比較したいことがありますね。そのために使われる値が偏差値です。そこで、偏差値の求め方と意味を見ていきましょう。

　平均値と標準偏差が異なっていると単純に比較はできないので、まず、それぞれの分布を、平均値0、標準偏差1の標準正規分布になるように値を調整します。そのために、各データxから平均値μを引き、標準偏差σで割ります。つまり、

という計算を行います。このような計算を行うことを標準化と呼び、zの値を標準得点（または、z値など）と呼びます。

　一般に、

という文字で表され、

という文字で表されます。ここでは、サンプルとして取り出された集団を母集団そのものと考えているので、μとσを使っています。

　例えば、20歳代の170cmという値を標準化すると、

となり、60歳代の170cmであれば、

となり、60歳代の170cmの方が集団の中での位置としては上位であることが分かります。

　ExcelではSTANDARDIZE関数の引数にxの値、平均値、標準偏差を指定すると標準得点が求められます。サンプルファイルの［偏差値］ワークシートを開いて、セルF4に=STANDARDIZE(E4,B4,C4)と入力して、セルF5にコピーしましょう。それぞれ、-0.22727...、0.433333...という結果が得られるはずです（図9）。数式を入力しても計算しても大した手間ではありませんが、関数を使った方が標準得点を求めていることが明確に分かりますね。

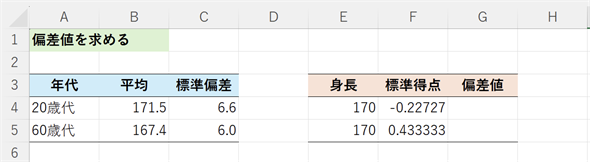図9　標準化を行って異なる集団の値同士を比較する
セルF4の値は=(E4-B4)/C4でも求められるが、=STANDARDIZE(E4,B4,C4)と入力した方が標準得点を求めていることが明確に分かる。セルF5にはセルF4の式をコピーすればよい。スピル機能を利用するなら、セルF4に=STANDARDIZE(E4:E5,B4:B5,C4:C5)と入力するだけでよい

　ところで、標準得点は0〜1の範囲の小数なので、私たちにとっては実感の湧きにくい値です。そこで、さらに平均が50、標準偏差が10になるように調整します。そのために、10を掛けて、50を足します。その値、つまり、標準得点×10＋50で求められる値が偏差値です。

　この式で計算すると、20歳代の170cmの偏差値は−0.2273 × 10＋50≈ 47.7となり、60歳代の170cmの偏差値は0.4333 × 10＋50≈ 54.33となります。Excelでも計算してみましょう（図10）。

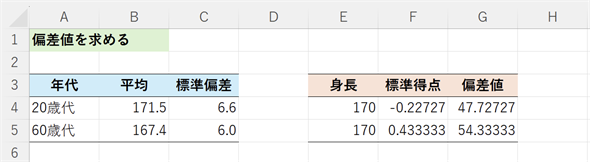図10　標準得点×10+50が偏差値
セルG4に=F4*10+50と入力し、セルG5にコピーすればそれぞれの偏差値が求められる。スピル機能を利用するなら、セルG4に=F4:F5*10+50と入力するだけでよい。平均が50になるので、日常的な感覚で比較しやすい値になる。

　上の例のように、平均値が異なると偏差値を求めなくてもある程度の察しは付きますが、平均値が等しい場合は判断しづらいですね。例えば、同じ調査で、30歳代の男性は身長の平均が171.5cm、標準偏差が5.5でした。40歳代の男性も身長の平均は171.5cmですが、標準偏差は5.8です。それぞれ、170cmの人の偏差値を求めてみましょう。

• 30歳代の170cmの人：

• 40歳代の170cmの人：

　というわけで、40歳代の170cmの人の方がわずかに上位にいるようです。Excelでの計算方法は図9と図10で見た例と同様です。入力例は［偏差値（完成例）］ワークシートをご参照ください。

上位10％に入るには何点取らないといけないのか 〜 累積分布関数の逆関数

　正規分布の逆関数を利用すれば、例えば、試験で上位何％の位置にいるには何点を取る必要があるのか、といった計算ができます。最初に見た、平均μ＝60、標準偏差σ＝10の正規分布で考えてみましょう。例えば、上位10％に入るために何点取らないといけないのかを求めてみます。

　上位10％ということは下位から90％（＝0.9）ということになりますね。0.9という累積確率を基に、累積分布関数の逆関数の値を求めようというわけです（図11）。

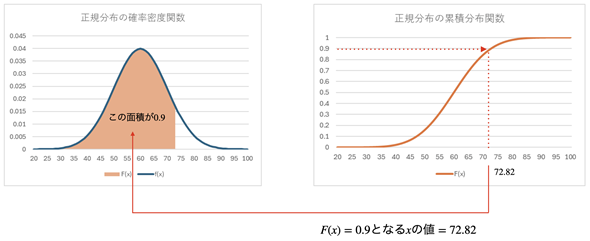図11　正規分布の累積分布関数に対する逆関数の値を求める
正規分布の累積分布関数（右側）で、縦軸の0.9という値から逆にたどっていけば、そのときのxの値が分かる（72.82となる）。この値は、確率密度関数（左側）のグラフとx軸で囲まれた範囲の面積が0.9になるときのxの値。

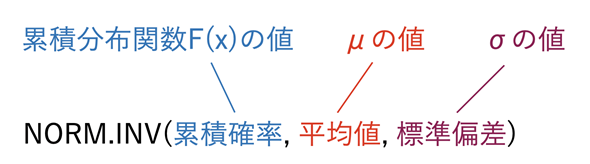
　すでに図11の中に答えが書いてありますが、正規分布の累積分布関数に対する逆関数の値を求めるNORM.INV関数を使って答えを求めてみましょう。［累積分布関数の逆関数］ワークシートを開いて、セルB7に=NORM.INV(A7,B3,B4)と入力してみてください。

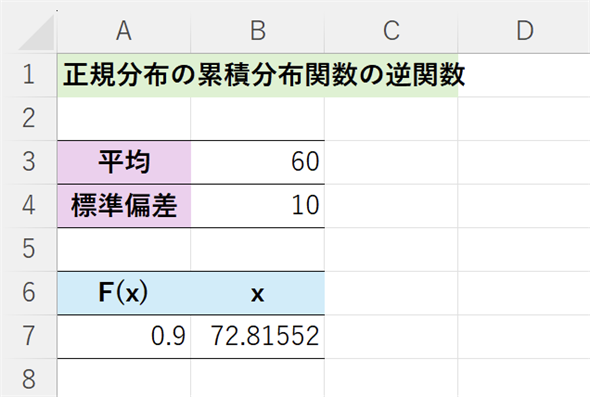図12　NORM.INV関数を使って累積分布関数に対する逆関数の値を求める
NORM.INV関数には、累積確率、平均、標準偏差を指定する。下位から90％（上位10％）の位置は72.82点であることが分かる。

　すでに見たとおり、結果は72.82点となります。72.82点以上取れば、上位10％以内に食い込めるというわけです。NORM.INV関数の引数は以下の図13のように指定します。

図13　NORM.INV関数に指定する引数
図12では、累積確率としてセルA7の0.9を指定し、平均値としてセルB3の60という値、標準偏差としてセルB4の10という値を指定している。

　正規分布の逆関数は、「母分散が既知の場合の母平均の検定」などでも使われます（推測統計編でお話しします）。なお、標準正規分布であれば、累積分布関数に対する逆関数の値を求めるのにNORM.S.INV関数関数が使えます（平均と標準偏差を指定する必要がないので簡単です）。

---

　さて、今回は正規分布の基本的な考え方や確率密度関数と累積分布関数の求め方、また、よく使われる理由や逆関数の求め方などについてお話ししました。正規分布は統計学のさまざまな場面で、これでもかというほど登場します。そういった例については、今後、関連のある箇所で少しずつ触れていくこととして、次回は、カイ二乗分布についてお話しします。

　カイ二乗分布は、標準得点を2乗和した値の分布で、理論的な値からのズレを求めたりするのに使われます。また、分散の比を表すF分布や、平均からどれだけ離れているかを表すのに使われるt分布とも深く関わっています。というわけで、次回もお楽しみに！

この記事で取り上げた関数の形式

　関数の利用例については、この記事の中で紹介している通りです。ここでは、今回取り上げた関数の基本的な機能と引数の指定方法だけを示しておきます。

正規分布の確率密度関数や累積分布関数の値を求めるための関数

NORM.DIST関数： 正規分布の確率密度関数や累積分布関数の値を求める

形式

NORM.DIST(x, 平均値, 標準偏差, 関数形式)

引数

• x： 確率変数の値を指定する。
• 平均値： 母集団の平均値μを指定する。
• 標準偏差： 母集団の標準偏差σを指定する。
• 関数形式： 以下の値を指定する。
  • ▲FALSE …… 確率密度関数の値を求める
  • ▲TRUE …… 累積分布関数の値を求める

NORM.S.DIST関数： 標準正規分布の確率密度関数や累積分布関数の値を求める

形式

NORM.S.DIST(x, 関数形式)

引数

• x： 確率変数の値を指定する。
• 関数形式： 以下の値を指定する。
  • FALSE …… 確率密度関数の値を求める
  • TRUE …… 累積分布関数の値を求める

備考

※ GoogleスプレッドシートのNORM.S.DIST関数には［関数形式］の引数が指定できません（累積分布関数の値のみが求められます）。

正規分布の累積分布関数に対する逆関数の値を求めるための関数

NORM.INV関数： 正規分布の累積分布関数に対する逆関数の値を求める

形式

NORM.INV(累積確率, 平均値, 標準偏差)

引数

• 累積確率： 累積分布関数の値を指定する。
• 平均値： 母集団の平均値μを指定する。
• 標準偏差： 母集団の標準偏差sigmaを指定する。

NORM.S.INV関数： 標準正規分布の累積分布関数に対する逆関数の値を求める

形式

NORM.S.INV(累積確率)

引数

• 累積確率： 累積分布関数の値を指定する。

標準化のための関数

STANDARDIZE関数：値を標準化する（標準得点を求める）

形式

STANDARDIZE(x, 平均値, 標準偏差)

引数

• x： 標準化したい値を指定する。
• 平均値： 母集団の平均値μを指定する。
• 標準偏差： 母集団の標準偏差σを指定する。

「やさしい確率分布」

AI・データサイエンスの学びをここから

初心者向け、データ分析・AI・機械学習・Pythonの勉強方法　＠ITのDeep Insiderで学ぼう