［データ分析］累積分布関数の逆関数 〜 95％の確率で推しのチケットを入手するまでに何回チャレンジすればいい？：やさしい確率分布

データ分析の初歩からステップアップしながら学んでいく連載（確率分布編）の番外編。代表的な離散型確率分布に対する累積分布関数の逆関数を紹介。例えば、二項分布の累積分布関数ではn回中k回まで成功する確率が求められますが、その逆関数では何％か（以上）の確率で成功するまでの回数を求められます。

[羽山博，著]

連載目次

連載：

『社会人1年生から学ぶ、やさしい確率分布』

　この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』連載（記述統計と回帰分析編）の続編で、確率分布に焦点を当てています。
　この確率分布編では、推測統計の基礎となるさまざまな確率分布の特徴や応用例を説明します。身近に使える表計算ソフト（Microsoft ExcelやGoogleスプレッドシート）を使いながら具体的に事例を見ていきます。
　必要に応じて、Pythonのプログラムや統計ソフト「R」などでの作成例にも触れることにします。
　数学などの前提知識は特に問いません。中学・高校の教科書レベルの数式が登場するかもしれませんが、必要に応じて説明を付け加えるのでご心配なく。肩の力を抜いてぜひとも気楽に読み進めてください。

羽山博

筆者紹介： IT系ライターの傍ら、非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。趣味の献血は心拍数が基準を超えてしまい99回で中断。心肺機能を高めるために水泳を始めるも、一向に上達せず。また、リターンライダーとして何十年ぶりかに大型バイクにまたがるも、やはり体力不足を痛感。足腰を鍛えるために最近は四股を踏む日々。超安全運転なので、原付やチャリに抜かされることもしばしば（すり抜けキケン、制限速度守ってね！）。

　データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の確率分布編、番外編です。前回までは、代表的な離散型確率分布の確率質量関数や累積分布関数の値を求める方法を見てきました。

　今回は、累積分布関数の逆関数を利用して、累積確率を基に、逆に確率変数の値kを求める方法を紹介します。「95％以上の確率で当選するのは何回までか」といった計算や、「95％以上の確率で当選するまでに何回チャレンジすればいいか」といった計算ができます。

ある確率以上となる確率変数の値kを求める 〜 累積分布関数の逆関数

　もったいぶるわけではありませんが「95％の確率で推しのチケットを入手するまでに何回チャレンジすればいい？」という表題の件については後回しにして、逆関数とは何かということからお話を始めます（逆関数の意味は知っているので、答えを知りたい、という方はこちらに進んでいただいても構いません）。

逆関数ってそもそも何だっけ？

　簡単な例から始めましょう。関数とはどのようなものものだったでしょうか。中学の数学では、

といった関数について学びました。xの値を指定するとyの値が1つに決まりますね。例えば、x＝3ならy＝6です。逆関数は、これとは逆にyの値からxの値を求める関数のことです。この例であれば、xについて解いて、

とすればいいですね。y＝6であればx＝3となります。

　高校の数学では、関数をy＝f(x)のように一般的に表すことがあります。このとき、逆関数は、関数名の右肩に−1を付けて、x＝f⁻¹(y)と表されます。具体例は後で見ますが、累積分布関数F(k)の値、つまり累積確率をPと表すと、kからP＝F(k)の値を求めるのとは逆に、Pからkの値を求めるので、F(k)の逆関数はF⁻¹(P)と表されます。

二項分布の累積分布関数についてのおさらい

　累積分布関数の逆関数も上で見たものと考え方は全く同じです。そこで、二項分布を例に、累積分布関数の逆関数がどのようなものかを見てみましょう。まずは、二項分布の累積分布関数のおさらいから始めます。二項分布の累積分布関数を利用すれば、例えば、p＝1/4の確率で当選するチケットにn＝10回申し込んだとき、k＝3回まで当選する確率などが求められます。

　k＝0〜10について、ExcelのBINOM.DIST関数を使って求めた累積分布関数の値とそれを折れ線グラフにした例を図1に示しました。セルB10を見れば、k＝3回まで当選する確率F(k)の値は0.776(＝77.6％)であることが分かります。0回当選する確率〜3回当選する確率の累計が77.6％であるということですね。

　二項分布は離散型確率分布なので、確率変数の値kはとびとびの値を取ります（0以上の整数となります）。「成功回数kが3.5回」などのような小数になることはないので、可視化する際には折れ線グラフよりも棒グラフの方が適しています。しかし、ここでは前回までに見た複合グラフの形式と合わせるために折れ線グラフにしてあります。

　BINOM.DIST関数の使い方やグラフの作成方法を忘れた方は、こちらでおさらいしてください。また、図1のサンプルファイルの［二項分布の累積分布関数］ワークシートにも図1の内容と作成手順が含まれているので、そちらもご参照くださいGoogleスプレッドシート用のサンプルファイルはこちらです。メニューから［ファイル］−［コピーを作成］を選択し、Googleドライブにコピーしてお使いください。これらのサンプルファイルには逆関数の例も含まれています（後でまた使います）。

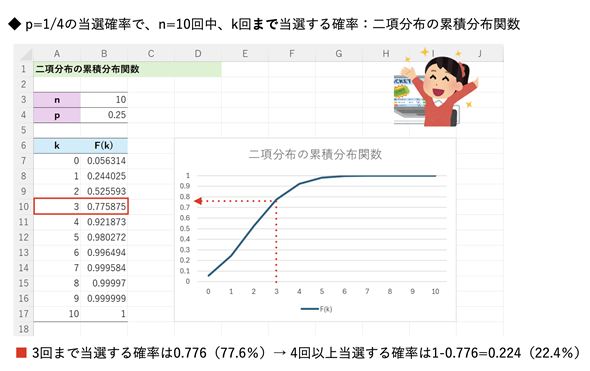図1　二項分布の累積分布関数で、確率変数の値kから累積確率を求める
累積分布関数では、kに対する累積確率F(k)の値が求められる。例えば、k＝3ならF(3)＝0.776となり、3回まで当選する確率は77.6％ということが分かる。このことから、4回以上当選する確率は1−0.776＝0.224（＝22.4％）であることも分かる。

　グラフでも確認しておきましょう。グラフの横軸は当選回数kで、縦軸はkに対するF(k)の値、つまり、二項分布の累積確率となっていますね。横軸のk＝3に対する縦軸の値はF(k)＝0.776であることが分かります（横軸の3のところから引かれている赤い点線で読み取れます）。いや、そこまで詳しくは分からないだろう、と思われるかもしれませんが、マウスポインターを折れ線の上に位置付けると、kに対するF(k)の値がポップアップ表示されるのでそのことが分かります。この確率を1から引くと、4回以上当選する確率（0.224）になることも分かりますね。

　0回当選する確率を含めても意味がないので、それは除外して、1〜3回当選する確率を求めたいということもありますね。そのような場合は、3回当選する累積確率から0回当選する累積確率を引けばいいのですが、ExcelのBINOM.DIST.RANGE関数を使えば、その値が簡単に求められます。図1の例であれば=B10-B7でも求められますが、=BINOM.DIST.RANGE(B3,B4,1,3)でも求められます。

二項分布の累積分布関数に対する逆関数とは

　累積分布関数とは逆の計算をしたいときもあります。つまり、逆関数により、累積確率P＝F(k)から確率変数の値kを求めたいということですね。例えば、n＝10回申し込んだときに、P＝95％以上の確率で当選するのは何回までかを求める、ということです。まずは図2のグラフで確認してみましょう。ワークシートは図1と同じものです。縦軸の0.95から逆にたどればいいですね。ブルーの点線をたどれば、5回までだということが読み取れそうです。B列の値を見ても、0.922（＝92.2％）に対するkの値が4、0.980（＝98.0％）に対するkの値が5であることから、間違いありません。

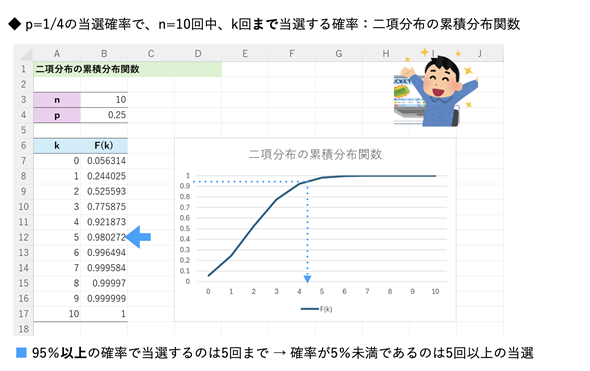図2　二項分布の累積分布関数で、累積確率から確率変数の値kを逆に読み取る
累積分布関数とは逆に、95％以上の確率で当選するのは何回までかを知りたいこともある。つまり、F(k)＝0.95以上となるkの値を求めるということ。グラフや表からk＝5であることが分かるが、表を作って目視で確認するのではなく、計算で求めたい（後述）。

　しかし、図2のような表やグラフを作って目視で確認するのではなく、ちゃんと計算で結果を求めたいですね。そこで、朗報です！　Excelでは二項分布の累積分布関数に対する逆関数の値を求めるBINOM.INV関数が利用できます。サンプルファイルの［二項分布の逆関数］ワークシートを開いて、セルE4に=BINOM.INV(B3,B4,D4)と入力してみてください（図3）。

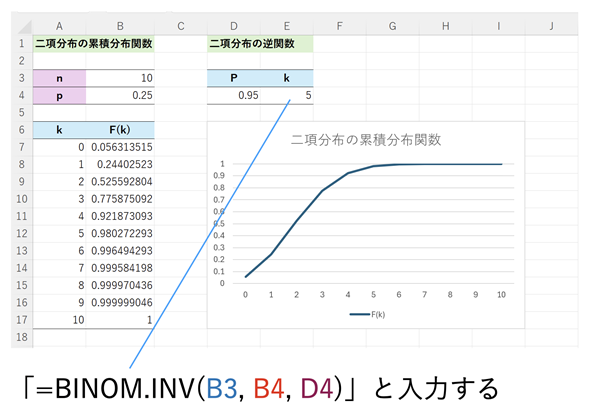図3　BINOM.INV関数により、二項分布の累積分布関数に対する逆関数の値を求める
BINOM.INV関数には、引数に試行回数nの値（セルB3）、1回の試行の成功確率pの値（セルB4）、累積確率P（セルD4）を指定する。結果は5となる。n＝10回申し込んだときに、P＝95％以上の確率で当選するのは5回まで。言い換えると、当選する確率が5％未満となるのは5回以上当選する場合。

　図3で入力したBINOM.INV関数の結果を見れば、n＝10回申し込んだときに、P＝95％以上の確率で当選するのは5回までということが分かります。従って、確率が5％未満であるのは5回以上当選する場合であることも分かります。もし、実際に5回以上当選したとすると、めったに起こらないことが起こった、ということになりますね。このような計算は、統計的検定を行う場合に使うのですが、検定のお話については、この連載の続編となる推測統計編でのお楽しみということにします。

　念のため、BINOM.INV関数に指定する引数を確認しておきましょう（図4）。

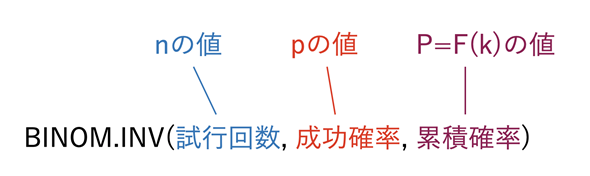図4　BINOM.INV関数に指定する引数
図3の例では、試行回数nの値としてセルB3（10という値）を指定、1回の試行の成功確率であるpの値としてセルB4（0.25という値）を指定、累積確率Pの値としてセルD4（0.95という値）を指定している。

95％の確率で推しのチケットを入手するまでに何回チャレンジすればいいのか？

　ここから、ようやく推しのチケットのお話です。人気アーティストのチケットが抽選販売となっていて、申し込んでもなかなか当選しないような状況を考えてみてください。k回目に1回成功（当選）する確率は幾何分布で求められました。前回のお話で登場した事例ですね。

　「95％の確率で推しのチケットを入手するまでに何回チャレンジすればいいのか」というのは、幾何分布の累積確率が95％以上となるのは、何回目に成功するまでなのか、ということです。従って、幾何分布の累積分布関数に対する逆関数で求められます。

• 幾何分布の累積分布関数： k回目までの試行で1回成功する累積確率Pを求める（kからPを求める）
• 幾何分布の累積分布関数に対する逆関数： 累積確率P以上で成功するまでの試行回数kは何回までかを求める（Pからkを求める）

　では、Excelの関数を使って……と言いたいところですが、Excelには幾何分布の確率質量関数の値や累積分布関数の値を求める関数もなければ、その逆関数の値を求める関数もありません。確率質量関数と累積分布関数については、負の二項分布の確率を求めるためのNEGBINOM.DIST関数で代用できますが、残念ながら、NEGBINOM.DIST関数の逆関数はありません。

　図2と同じような累積分布関数の表を作成して、そこから読み取るというのも手ですが、Pythonなどのプログラミング言語を使うと簡単です。毎回の当選確率を1/4（4分の1）とすれば、以下のコード（リスト1）で答えが得られます。SciPyは科学技術計算を行うためのライブラリで、scipy.statsは特に統計的な計算を行うためのモジュールとなっています。

　Excelのゴールシーク（＝目標の計算結果を得るために必要な値を逆算する機能）を使うという方法もあります。しかし、NEGBINOM.DIST関数を使うと残念ながら計算が収束せず、答えが得られません（kの値が整数であるため）。

　実は、ベータ分布の確率密度関数や累積分布関数を求めるためのBETA.DIST関数を使って、パラメーターαに1を、βにkの値を指定すれば、幾何分布の累積確率が求められます。それに対してゴールシークを適用すれば答えが求められます。

　ベータ分布は連続型確率分布なので、今回はこれ以上は触れません（次回以降をお楽しみに！）。入力例やゴールシークの方法については、サンプルファイルの［幾何分布］ワークシートに含めてあるので、興味のある方はご参照ください。

　サンプルプログラムはこちらから参照できます。リンクをクリックすれば、ブラウザが起動し、Google Colaboratoryの画面が表示されます。

　リスト1に示したPythonコードは2つのコードセル（＝プログラムコードを入力して実行できる領域）に入力されています（Googleアカウントでのログインが必要です）。コードセルをクリックして［Shift］+［Enter］キーを押せばコードが実行できます。ここで求めたい答えを得るためには2つ目のコードセルを実行するだけで構いません。が、以降のコードセルでグラフ作成などを行うので、1つ目のコードセルを実行した上で、2つ目のコードセルを実行してください。

# 1つ目のコードセルの内容：
# 以下のモジュールは、これ以降、グラフ作成などで使われるので、最初に必ず1回実行しておくこと
import matplotlib.pyplot as plt
import numpy as np

# 2つ目のコードセルの内容：
# 毎回の当選確率を1/4とする
from scipy.stats import geom

geom.ppf(0.95, 1/4)  # 累積確率、毎回の成功確率を指定
# 出力例：
# 11.0

リスト1　95％の確率で推しのチケットに当選するまでの落選回数を求める
scipy.statsモジュールで利用できる統計関数では、それぞれの分布を表すクラスの、pmfという関数が確率質量関数（連続型確率分布の場合はpdfという関数が確率密度関数）、cdfという関数が累積分布関数、ppfという関数が確率質量関数の逆関数となっている。幾何分布については、geom.ppfという関数が累積分布関数に対する逆関数。この関数に累積確率と毎回の試行での成功確率を指定すれば、その累積確率以上になるまでの失敗数が求められる。

　scipy.statsモジュールのgeomが、幾何分布を表すクラスです。そのgeom.ppf関数が、累積分布関数に対する逆関数となります。この関数に累積確率と毎回の試行での成功確率を指定すれば、その累積確率以上になるまでの失敗数が求められます。

　リスト1のgeom.ppf(0.95, 1/4)関数を実行すると11.0という結果が出力されます。つまり、95％の累積確率以上になるまでの失敗数が11回という結果です。

　いきなり当選することもあれば、何回申し込んでも落選ということもあるかもしれませんが、この結果から、理論的には95％の確率で、11回までの落選の後に（つまり12回目までに）当選するものと考えられます。それ以上チャレンジしても当選しないということは、各試行の当選確率である1/4という前提が誤っていると考えられます（たまたま、という可能性もあります）。

大谷選手が95％の確率で50本のホームランを打つまでの打席数は？

　前回、大谷選手のホームラン数が50本になるまでの打席数とその確率を求めました。その際に利用したのが負の二項分布です。負の二項分布はn回成功するまでにk回失敗する確率の分布でしたね。これについても、逆関数を利用すれば、95％の確率で50本のホームランを打つまでに、ホームランでない打席数は何回までになるかが求められます。

　残念ながら、負の二項分布についても、累積分布関数の逆関数はExcelにはありません。リスト1と同様に、scipy.statsモジュールのnbinom.ppf関数を使いましょう。上と同じサンプルプログラムの3つ目のコードセルにリスト2のコードが入力されています。コードセルをクリックし、［Shift］+［Enter］キーを押せば実行できます。

from scipy.stats import nbinom

p = 26/375  # 打席数に対するホームランの確率
nbinom.ppf(0.95, 50, p)  # 累積確率、成功数、毎回の成功確率を指定
# 出力例：
# 841.0

リスト2　95％の確率で50本のホームランを打つまでの打席数を求める
負の二項分布では、nbinom.ppf関数を利用すれば累積分布関数の逆関数の値が求められる。引数には、累積確率と成功数、毎回の試行での成功確率を指定する。累積確率以上で指定した回数だけ成功するまでの失敗数が求められる。

　前回の原稿執筆時には、375打席中26本のホームランを打っていたので、毎回の成功確率を26/375としました。リスト2のgeom.ppf関数を実行すると841.0という値が出力されます。その結果から、95％以上の確率で50本のホームランを打つまでの、ホームランでない打席数は841と考えられます。従って、95％以上の確率で50本のホームランを打つまでの打席数は、理論上、841＋50＝891打席となります。

　もっとも、前回の記事の最後にも記したように、メジャーリーグの全試合は約160試合なので、全ての試合で4回の打席に立ったとしても、640打席しかありません。ということは、95％という高い確率でシーズン中に50本のホームランを打つということは難しいようです。もちろん、ムリだということではなく、この時点ではほぼ確実だと言うのが難しいということです。

　ちなみに、この原稿の執筆時点では、ホームラン数は429打席中29本となっています（オールスターでもホームランを打ちましたが、公式戦での記録には含まれません）。

確率分布と逆関数のいろいろ

　Excelでは、累積分布関数の逆関数として以下のようなものが利用できます（表1）。表には、これまでに見てきた離散型確率分布だけでなく、連続型確率分布の逆関数も掲載しておきました。連続型確率分布については、次回以降解説するので、ここでは名前の掲載だけにとどめておきます。太字の分布と関数が既出のものです。

◆ 離散型確率分布

確率分布	Excelでの関数	Excelでの累積分布関数の逆関数
二項分布	BINOM.DIST, BINOM.DIST.BETWEEN	BINOM.INV
超幾何分布	HYPGEOM.DIST	なし
ポアソン分布	POISSON.DIST	なし
幾何分布	なし（NEGBINOM.DISTで代用可能）	なし（Pythonでの方法を上で紹介）
負の二項分布	NEGBINOM.DIST	なし（Pythonでの方法を上で紹介）
負の超幾何分布	なし	なし

◆ 連続型確率分布

確率分布	Excelでの関数	Excelでの逆関数
正規分布	NORM.DIST	NORM.INV
標準正規分布	NORM.S.DIST	NORM.S.INV
対数正規分布	LOGNORM.DIST	LOGNORM.INV
カイ二乗分布	CHISQ.DIST, CHISQ.DIST.RT	CHISQ.INV, CHISQ.INV.RT
t分布	T.DIST, T.DIST.2T, T.DIST.RT	T.INV, T.INV.2T
F分布	F.DIST, F.DIST.RT	F.INV, F.INV.RT
指数分布	EXPON.DIST	なし
ガンマ分布	GAMMA.DIST	GAMMA.INV
ベータ分布	BETA.DIST	BETA.INV
ワイブル分布	WEIBULL.DIST	なし

表1　確率分布を求めるための関数と、累積分布関数の逆関数
確率分布とExcelで利用できる関数、逆関数の一覧。離散確率分布のうち、Excelでの関数が用意されていないものについては、Pythonなどのプログラミング言語を使って求めるのが簡単。「なし」と書かれているものについては、サンプルプログラムの中に利用例が含まれているので、そちらを参照のこと。

　表1の離散型確率分布については、累積分布関数のグラフを作成するためのコードと、その逆関数の値を求めるためのコードを、上で紹介したGoogle Colaboratoryでのサンプルプログラムに全て含めてあります。興味のある方はぜひご参照ください。

　負の超幾何分布については、確率質量関数や累積分布関数を求めるための関数がExcelには用意されていないので、この連載でも触れませんでしたが、そらちについてもサンプルプログラムに含めてあります。負の超幾何分布は、負の二項分布と似ていますが、非復元抽出の場合の確率分布です。

• 負の二項分布： n回成功するまでにk回失敗する確率（復元抽出）
• 負の超幾何分布： n回成功するまでにk回失敗する確率（非復元抽出）

---

　今回は、累積分布関数の逆関数についてお話ししました。例えば、95％以上の確率で（ほぼ確実に）成功するのは何回までかを求めたり、逆に、5％未満の確率でしか成功しないのは何回以上なのかを求めたりできるので、応用の幅が広がりますね。

　逆関数は、とりわけ、次回以降から始まる連続型確率分布でも重要になってきます。例えば、試験で上位5％に入るには何点取らないといけないか、といったことが求められます。知りたいですよね！　また、上で少し触れたように、統計的検定の計算でも累積分布関数の逆関数が使われます。

　というわけで、次回から連続型確率分布のお話に移りたいと思います。連続型確率分布の代表とも言える正規分布からスタートします。では、次回もお楽しみに！

この記事で取り上げた関数の形式

　関数の利用例については、この記事の中で紹介している通りです。ここでは、今回取り上げた関数の基本的な機能と引数の指定方法だけを示しておきます。

二項分布の累積分布関数の値を求めるための関数（確率変数の範囲を指定）

BINOM.DIST.RANGE関数： 確率変数の値を指定して二項分布の累積分布関数の値を求める

形式

BINOM.DIST.RANGE(試行回数, 成功確率, 成功数1, 成功数2)

引数

• 試行回数： 試行の回数（nの値）を指定する。
• 成功確率： 1回の試行で目的の事象が起こる確率を指定する。
• 成功数1： 成功数の下限を指定する。
• 成功数2： 成功数の上限を指定する。省略すると、成功率1と同じ値が指定されたものと見なされる（成功数1の確率質量関数の値が返される）。

二項分布の累積分布関数に対する逆関数の値を求めるための関数

BINOM.INV関数： 二項分布の累積分布関数に対する逆関数の値を求める

形式

BINOM.INV(試行回数, 成功確率, 累積確率)

引数

• 試行回数： 試行の回数（nの値）を指定する。
• 成功確率： 1回の試行で目的の事象が起こる確率を指定する。
• 累積確率： 累積確率を指定する。累積分布関数の値がここで指定した累積確率以上になるk（成功数）はいくらまでかが求められる。

「やさしい確率分布」

AI・データサイエンスの学びをここから

初心者向け、データ分析・AI・機械学習・Pythonの勉強方法　＠ITのDeep Insiderで学ぼう