[解決!Python]dequeオブジェクトを使うには:解決!Python
Pythonに標準で付属するcollectionsモジュールには、両端の要素へのアクセスを高速に行えるコンテナであるdeque(デック)クラスが含まれている。その基本的な使い方を紹介する。
from collections import deque
# dequeを作成する
d = deque([0, 1, 2, 3, 4])
print(d) # deque([0, 1, 2, 3, 4])
# 最大要素数を指定してdequeを作成する
d = deque([0, 1, 2, 3, 4], maxlen=10)
print(d) # deque([0, 1, 2, 3, 4], maxlen=10)
# dequeの右端に要素を追加
d.append(5)
print(d) # deque([0, 1, 2, 3, 4, 5], maxlen=10)
# dequeの左端に要素を追加
d.appendleft(-1)
print(d) # deque([-1, 0, 1, 2, 3, 4, 5], maxlen=10)
# dequeの右端に反復可能オブジェクトの要素を追加
d.extend([6, 7, 8])
print(d) # deque([-1, 0, 1, 2, 3, 4, 5, 6, 7, 8], maxlen=10)
# dequeの左端に反復可能オブジェクトの要素を追加
d.extendleft([-2, -3, -4])
print(d) # deque([-4, -3, -2, -1, 0, 1, 2, 3, 4, 5], maxlen=10)
d.append(6)
print(d) # deque([-3, -2, -1, 0, 1, 2, 3, 4, 5, 6], maxlen=10)
# dequeの右端から要素を取り出す
print(d.pop()) # 6
print(d) # deque([-3, -2, -1, 0, 1, 2, 3, 4, 5], maxlen=10)
# dequeの左端から要素を取り出す
print(d.popleft()) # -3
print(d) # deque([-2, -1, 0, 1, 2, 3, 4, 5], maxlen=10)
# dequeを右にローテートする
d.rotate(2)
print(d) # deque([4, 5, -2, -1, 0, 1, 2, 3], maxlen=10)
# dequeを左にローテートする
d.rotate(-2)
print(d) # deque([-2, -1, 0, 1, 2, 3, 4, 5], maxlen=10)
# dequeの要素アクセスにかかる時間を調べる
import time
# 中央の要素
def test_access_to_middle(d):
mid_pos = len(d) // 2
t_list = []
for i in range(10):
t0 = time.time()
for n in range(100000):
_ = d[mid_pos]
t1 = time.time()
t_list.append(t1 - t0)
return t_list
d0 = deque(range(10))
t_list0 = test_access_to_middle(d0)
avg0 = sum(t_list0) / len(t_list0)
print(avg0)
d1 = deque(range(100000))
t_list1 = test_access_to_middle(d1)
avg1 = sum(t_list1) / len(t_list1)
print(avg1)
print(avg1 - avg0)
# 先頭の要素
def test_access_to_first(d):
t_list = []
for i in range(10):
t0 = time.time()
for n in range(100000):
d.appendleft(0) # 左端(先頭、インデックス0)に要素を追加
d.popleft() # 左端(先頭、インデックス0)の要素をポップ
t1 = time.time()
t_list.append(t1 - t0)
return t_list
d0 = deque(range(10))
t_list0 = test_access_to_first(d0)
avg0 = sum(t_list0) / len(t_list0)
print(avg0)
d1 = deque(range(100000))
t_list1 = test_access_to_first(d1)
avg1 = sum(t_list1) / len(t_list1)
print(avg1)
print(avg1 - avg0)
# 末尾の要素
def test_access_to_last(d):
t_list = []
for i in range(10):
t0 = time.time()
for n in range(100000):
d.append(0) # 右端(末尾に要素を追加
d.pop() # 右端(末尾)の要素をポップ
t1 = time.time()
t_list.append(t1 - t0)
return t_list
d0 = deque(range(10))
t_list0 = test_access_to_last(d0)
avg0 = sum(t_list0) / len(t_list0)
print(avg0)
d1 = deque(range(100000))
t_list1 = test_access_to_last(d1)
avg1 = sum(t_list1) / len(t_list1)
print(avg1)
print(avg1 - avg0)
deque(デック)とは
Pythonに標準で付属するcollectionsモジュールにはdequeクラスが含まれている。deque(デック)とはリストに似たコンテナ型であり、任意の値をその要素にできる。ドキュメントでは「スタックとキューを一般化したもの」と書いてあるが、その先頭や末尾への要素の追加、先頭や末尾の要素の削除などを高速に行えることを意味する(中間にある要素へのアクセスは得意ではない。後述)。
dequeクラスのインスタンスを作成するには、collectionsモジュールからこのクラスをインポートして、反復可能オブジェクトを渡す。以下に例を示す。
from collections import deque
d = deque([0, 1, 2, 3, 4])
print(d) # deque([0, 1, 2, 3, 4])
ここでは[0, 1, 2, 3, 4]というリストを渡すことで、deque([0, 1, 2, 3, 4])というオブジェクトが作成されている。反復可能オブジェクトを渡さなければ、空のdequeオブジェクトが作成される。
dequeオブジェクトの作成時には最大の要素数を指定することも可能だ。これにはmaxlenパラメーターに最大の要素数を指定する。
d = deque([0, 1, 2, 3, 4], maxlen=10)
print(d) # deque([0, 1, 2, 3, 4], maxlen=10)
ここではmaxlenパラメーターに10を渡しているので、このdequeオブジェクトの最大の要素数は10となる。以下では、このdeque([0, 1, 2, 3, 4], maxlen=10)を例にdequeオブジェクトの基本的な操作を見ていく。
要素の追加
通常のリストとは異なり、dequeクラスはappendメソッドに加え、appendleftメソッドを持っている。appendメソッドはdequeオブジェクトの右端(末尾)に要素を追加し、appendleftメソッドはdequeオブジェクトの左端(先頭)に要素を追加する。
# dequeの右端に要素を追加
d.append(5)
print(d) # deque([0, 1, 2, 3, 4, 5], maxlen=10)
# dequeの左端に要素を追加
d.appendleft(-1)
print(d) # deque([-1, 0, 1, 2, 3, 4, 5], maxlen=10)
同様に、extendメソッドと対になるextendleftメソッドもある。これらはメソッドに渡して反復可能オブジェクトの要素をdequeオブジェクトの要素として追加するものだ。
# dequeの右端に反復可能オブジェクトの要素を追加
d.extend([6, 7, 8])
print(d) # deque([-1, 0, 1, 2, 3, 4, 5, 6, 7, 8], maxlen=10)
# dequeの左端に反復可能オブジェクトの要素を追加
d.extendleft([-2, -3, -4])
print(d) # deque([-4, -3, -2, -1, 0, 1, 2, 3, 4, 5], maxlen=10)
こうした振る舞いは、要素を追加する場所を除けば、リストのappendメソッドやextendメソッドと同様なので、特に難しいところはないだろう。
ただし、上の例でdequeオブジェクトの要素数が10になった点に注意してほしい。この時点でappendメソッドを呼び出すとどうなるか見てみよう。
d.append(6)
print(d) # deque([-3, -2, -1, 0, 1, 2, 3, 4, 5, 6], maxlen=10)
appendメソッドはdequeオブジェクトの右端に要素を追加するが、これにより左端の要素が1つ削除されているのに注目されたい。ここでは示さないが、appendleftメソッドで要素を左端に追加したときに、最大要素数を超えると右端の要素が削除される。extendメソッドとextendleftメソッドでも同様な振る舞いとなる。
要素の削除
要素を取り出して、dequeオブジェクトから削除するにはpopメソッドとpopleftメソッドが使える。
# dequeの右端から要素を取り出す
print(d.pop()) # 6
print(d) # deque([-3, -2, -1, 0, 1, 2, 3, 4, 5], maxlen=10)
# dequeの左端から要素を取り出す
print(d.popleft()) # -3
print(d) # deque([-2, -1, 0, 1, 2, 3, 4, 5], maxlen=10)
del文による要素の削除も可能だ(例:del d[2])。
要素のローテート
dequeクラスに特有のメソッドとしてはrotateメソッドがある。このメソッドに正の整数を与えると、その分だけ要素を右にローテートする。
d.rotate(2)
print(d) # deque([4, 5, -2, -1, 0, 1, 2, 3], maxlen=10)
逆に負の整数を与えると要素を左にローテートする。
d.rotate(-2)
print(d) # deque([-2, -1, 0, 1, 2, 3, 4, 5], maxlen=10)
dequeオブジェクトはスライスをサポートしていない。そのため、スライスと同様な操作をするときには、rotateメソッドでdequeオブジェクトをローテートすると便利なことがある。例えば、スライスの先頭とステップを指定して、要素を取り出し、それらを要素とするdequeオブジェクトを作成する次のような関数が考えられる(ループの終了処理などはもっとエレガントに書けるかもしれないが、筆者が思い付きで書いただけなので、汚いコードになっていることはご容赦願いたい)。
def slice_deque(d, start, step):
cp = d.copy()
ln = len(cp) - start
stop = ln // step if ln % step == 0 else ln // step + 1
result = deque()
cp.rotate(-start)
for _ in range(stop):
result.append(cp.popleft())
cp.rotate(-(step-1))
return result
d_tmp = deque(range(10))
print(slice_deque(d_tmp, 0, 2)) # deque([0, 2, 4, 6, 8])
print(slice_deque(d_tmp, 0, 3)) # deque([0, 3, 6, 9])
print(slice_deque(d_tmp, 2, 3)) # deque([2, 5, 8])
ただし、上記のコードであれば、dequeオブジェクトをリストに変換して、そのスライスを得てから、再度dequeオブジェクトを作成する方が簡単ではある。
その他の処理
これらのメソッド以外にも通常のリストと同様なメソッドもあるが、これらについては説明を省略する。
- clearメソッド:全ての要素を削除
- copyメソッド:dequeオブジェクトの浅いコピーを作成する
- countメソッド:指定した値がdequeオブジェクトに含まれている数を調べる
- indexメソッド:指定した値がdequeオブジェクトのどこにあるかを調べ、あればそのインデックスを返し、なければValueError例外を発生させる
- insertメソッド:指定した位置に指定した値の要素を挿入する(最大要素数を超えるときにはIndexError例外を発生させる)
- removeメソッド:dequeオブジェクトから指定した値のうちインデックスが一番小さいものを削除する。なければValueError例外を発生させる
- reverseメソッド:要素を逆順に並べ替える(インプレース処理)
この他、最大要素数を調べるmaxlen属性もある。
dequeの要素アクセスにかかる時間を調べる
冒頭でdequeオブジェクトはコンテナの末端(先頭と末尾)での要素アクセスが高速で、途中の要素へのアクセスは得意ではないと書いたが、本当にそうなるかを試してみよう。
以下は、中央の要素へのアクセスにかかる時間を計測する関数だ。
import time
def test_access_to_middle(d):
mid_pos = len(d) // 2
t_list = []
for i in range(10):
t0 = time.time()
for n in range(100000):
_ = d[mid_pos]
t1 = time.time()
t_list.append(t1 - t0)
return t_list
ここではdequeオブジェクトの中央要素にインデックスでアクセスする処理を10万回繰り返すのにかかる時間を計測している。この計測を10回行い、その結果を含むリストを返すものだ。
この関数に要素数10のdequeオブジェクトと、要素数10万のdequeオブジェクトを渡し、それぞれの平均実行時間を求めるのが以下のコードだ。
d0 = deque(range(10))
t_list0 = test_access_to_middle(d0)
avg0 = sum(t_list0) / len(t_list0)
print(avg0)
d1 = deque(range(100000))
t_list1 = test_access_to_middle(d1)
avg1 = sum(t_list1) / len(t_list1)
print(avg1)
print(avg1 - avg0)
これを実行した結果を以下に示す。
avg0の値は要素数10のdequeオブジェクトにおける中央要素へのアクセス時間の計測結果を平均したもので、要素数10万のdequeオブジェクトでの計測結果を平均したavg1と比べて圧倒的に短時間で処理が終わっていることに注目されたい。
次に先頭要素へのアクセスについても見てみる(Pythonのドキュメントでは「添字によるアクセスは、両端の要素では O(1) ですが、中央部分の要素では O(n) と遅くなります」とあるので、本来であればインデックスアクセスを試すべきかもしれないが、ここではappendleftメソッドとpopleftメソッドを使用している)。
関数についての説明は省略する。先と同様に(ただし、アクセス位置を先頭にして)要素数10と10万のdequeオブジェクトの要素アクセスにかかる時間を計測した。
def test_access_to_first(d):
t_list = []
for i in range(10):
t0 = time.time()
for n in range(100000):
d.appendleft(0) # 左端(先頭、インデックス0)に要素を追加
d.popleft() # 左端(先頭、インデックス0)の要素をポップ
t1 = time.time()
t_list.append(t1 - t0)
return t_list
d0 = deque(range(10))
t_list0 = test_access_to_first(d0)
avg0 = sum(t_list0) / len(t_list0)
print(avg0)
d1 = deque(range(100000))
t_list1 = test_access_to_first(d1)
avg1 = sum(t_list1) / len(t_list1)
print(avg1)
print(avg1 - avg0)
実行結果を以下に示す。
要素数に関係なく高速に先頭要素へアクセスできていることが分かる。
末尾要素についても同様だ(実行結果は省略する)。
def test_access_to_last(d):
t_list = []
for i in range(10):
t0 = time.time()
for n in range(100000):
d.append(0) # 右端(末尾に要素を追加
d.pop() # 右端(末尾)の要素をポップ
t1 = time.time()
t_list.append(t1 - t0)
return t_list
d0 = deque(range(10))
t_list0 = test_access_to_last(d0)
avg0 = sum(t_list0) / len(t_list0)
print(avg0)
d1 = deque(range(100000))
t_list1 = test_access_to_last(d1)
avg1 = sum(t_list1) / len(t_list1)
print(avg1)
print(avg1 - avg0)
Copyright© Digital Advantage Corp. All Rights Reserved.

 要素数が少ない方が中央要素へのアクセスが高速
要素数が少ない方が中央要素へのアクセスが高速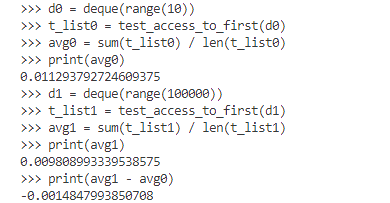 要素数に関係なく高速にアクセスできている
要素数に関係なく高速にアクセスできている



