[AI・機械学習の数学]文字式を使いこなせば一気にレベルアップ:AI・機械学習の数学入門(1/3 ページ)
数字(1、2、3、……)の式の次は、文字(a、b、x、y、……)を使った式をおさらいしよう。これまでに学んだ知識と平方完成を使って、距離の二乗和の最小値を求める計算も行う。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
前回は、「機械学習なんて人間が日常やっていることとそう変わらない」とか、「機械学習で使われる数学といっても結局のところ四則演算とその延長でしかない」といったお話をしました。簡単な例として、距離を求める方法について、具体的な数字を使った計算もやってみました。
今回は具体的な数字ではなく、
- 一般的な数を表したいときに便利な「文字式」(目標【その1】)
- 目的に合わせて文字式を変形する方法(目標【その2】)
をおさらいします。文字式を使いこなせると、数式で表現できる世界が一気に広がります。また、方程式や関数についてもさらっと(しれっと?)取りあげ、問題を簡単に解決するための基本を身に付けます。
目標【その1】: 文字式に慣れる
今回の目標の1つ目は文字式に慣れることです。具体的な数の代わりに、文字を使って式を表せば物事をより一般的に説明できるようになります。プログラミングでは何らかの値を表すのにcountやsumといった単語を変数名として使うのが一般的ですが、数学では1つの数は原則として1文字で表します*1。どの文字を何のために使うかということについては、厳密なルールはありませんが、以下のような使われ方をします。
- a,b,cなど …… 一般的な定数(何らかの決まった値)として使うことが多い
- x,y,z,tなど …… 変数(さまざまな値を取る)として使うことが多い
必ずしも、上に記した目的の通りに使われるわけではありませんし、これ以外の使われ方もあります(必要に応じてその都度説明します)が、文字がどのような目的で使われているかを意識していれば、式を見たときにだいたいの意味が分かります。また、違和感があるときには、違った意味で使われているかもしれない、ということも分かります。
ともあれ、まずは文字式に慣れるために、簡単な例を使って見ていきましょう。
*1 i,j,kなどは、後述する添字(そえじ: 「何番目の値か」ということを表すための文字)として使われることがよくあります。添字はai のように、文字の右下に小さく書くのが一般的です。この場合、厳密には2つの文字で1つの値を表していることになります。
解説:数の代わりに文字を使う
今回もやはり小学校のレベルからスタートします。最初は、文字式を使わずに、具体的な数字を使って平均値(算術平均)を求めてみましょう。小学校のレベルとはいえ、平均値を求める計算は、機械学習に限らずあらゆるデータ処理に必須です。
では、例題です。56と78と91という3つのデータの平均値を求める式を書いてみてください。計算結果は書かなくても構いません。
平均値の計算方法は数値を全て足して、個数で割るです。答えは、
です。ちなみに計算結果は75.0です。カンタンでしたね。
次は、中学校の数学です。中学に入ると、文字式を学ぶので、数字の代わりにaとかbといった文字を使うようになります。
では、56とか78とか91といった数字の代わりに、文字を使ってみます。aとbとcの平均を求める式を書いてみましょう。読んでいるだけというのも退屈ですし、ついつい読むペースも速くなってしまうので、穴埋め問題にしてみましょう。答えは、オレンジ色の部分をそれぞれクリック(またはタップ)すると表示されます。
a + b + c
───────────
3
はい、これもカンタンでした。a,b,cは、どういう値か取りあえずは分からないけれど、何らかの決まった値です。最初に言ったように、何らかの値の代わりに文字を使うというだけのことです*2。
文字式ではさまざまな文字が値の代わりに使われますが、
は英語の筆記体とは違う書き方をすることがよくあります。これはギリシア文字の
と混同するのを避けるためです(図1)。
*2 「数」の「代」わり、だから「代数」と呼ばれますね。ちなみに、文字式でも結局は四則演算をやっているだけです。今回の内容も四則演算ができれば全て理解できます。
*余談 ちょっと余談です。数学に対する苦手意識を生みだす原因の一つにπ,σ,θ といったギリシア文字があるかもしれませんね。
ギリシア文字の小文字は、意味のある定数(=決まった値)を表すのによく使われます。例えば、π(パイ)は円周率を表すのに使われ、σ(シグマ)は母集団の標準偏差を表すのに使われます。θ(シータ)は角度を表すのに使われます。また、θは、機械学習では変数の「重み」(影響の大きさ)を表すのに使われることもあります。
πはご存じのように3.141592...という特定の値ですが、σやθは、3.141592...のような特定の値ではありません。基となるデータや状況によって異なるかもしれませんが、何らかの決まった値ということです。なお、ギリシア文字ではありませんが、自然対数の底と呼ばれる値はeと表します。この値は、2.718281...という特定の値です。
ギリシア文字は確かになじみがないかもしれませんが、このような文字の用途や意味合いの違いを抜きにして、「この角度をθとすると」というように、呪文のような文字が数学の教科書にいきなり登場したことで、面食らった人も多いのではないかと思います(実際には、数学の授業で丁寧に説明されているのかもしれませんが、残念なことに私の記憶には残っていません)。
目標【その2】: 文字式の計算に便利な公式を利用する
計算の方法については、前回に見た四則演算の記号(+,−,×,÷)やべき乗の表記がそのまま使えます。ただし、掛け算の記号(×)は省略するか、⋅で代用できます。
- a× bはabまたは、a⋅ bと表せる
文字式の計算を簡単にするためにさまざまな公式が使えますが、ここでは必要最低限ということで、分配法則と二乗の展開公式を見ておきましょう。
- 分配法則:
- 二乗の展開公式:
この2つの公式について解説します。
解説:文字式の計算
上にも示したように、文字式の計算では、掛け算の記号が省略できます。例えば、
です。数字の場合、3 × 4の×を省略して34と書いてしまうと「さんじゅうよん」と間違ってしまいます。しかし、abならa × bであることが明らかです。なお、3 × 4を3 ⋅ 4のように省略して書くこともあります。数学者には、書く手間を少しでも省きたいという面倒くさがりな人が多いのかもしれませんね。
分配法則については、前回紹介しました。文字式の四則演算でも分配法則が使えます。
(※分配法則の計算過程を分かりやすく解説する音声解説付き動画も用意しました! 必要に応じてご視聴ください。)
動画1 分配法則の計算
念のため、
に数値を当てはめて確認しておきましょう。以下の式では、
- 3が、(1)式のaに当たり
- 4が、(1)式のxに当たり
- 5が、(1)式のyに当たり
ます。慣れないうちは、どれがどれに対応しているかを「指さし確認」する習慣を付けるといいと思います。が、すぐに慣れるはずです。
(例)
[A]のアンダーラインを引いた部分は(1)式の左辺と同じ形です。一方、[B]のアンダーラインを引いた部分は(1)式の右辺と同じ形になっています*3。確かに結果は同じですね。
*3 等号(=)や不等号(<,≦,≧,>)の左側の式を左辺、右側の式を右辺と呼びます。念のため。なお、「≦」と「≤」は同じ意味です。「≧」と「≥」も同じ意味です。
ただし、たまたまこの値だとうまくいったからかもしれないので、(1)式が成り立つことを示しておくと、以下の通りになります(※解説動画を用意しましたので、必要に応じてご視聴ください)。
動画2 分配法則の証明
掛け算を足し算に戻して考えるといいですね。
- [A] …… aを掛けるということは、a回足すということ
- [B] …… 足し算は順序を変えても同じなので、同類項で(xはxで、yはyで)まとめた
- [C] …… xをa回足したものは、x掛けるaなので、xaと表せる。掛け算は順序を変えても同じなのでaxと書いてもよい(一般に、アルファベットの順に書きます)
この公式を利用すると、以下のような公式も導き出せます。いちいち証明はしませんが、特に下の公式(二乗の展開公式)は機械学習でよく使うので、ぜひ覚えておきましょう……と言いたいところですが、覚えておく必要はありません。ここに書いてある、ということだけを覚えておけば十分です。
(なお、解説動画では、これらの公式が成り立つことも説明しています。)
動画3 式の展開
これらの公式は、中学校で数学の基礎として学びますね。こういった公式を使って式を展開したり、因数分解したり……と無味乾燥な計算を延々とやらされて、こんなのがいったい何の役に立つんだろう、とうんざりしていた人も多いと思います。念のため確認しておくと、式の展開は以下の図2で左辺を右辺のように変形すること、因数分解は右辺を左辺のように変形することでした(因数分解とは何か、という定義を説明しても抽象的になりすぎて実感が湧かないでしょうから、あとの練習問題で少し具体例を見ます)。
でも、機械学習のための数学ではこのような計算をよく使うのです。回帰式を求めるときに「あれ、なんだこれ二乗の展開公式使ってるじゃん」と気が付いたり、共分散を求めるときに「内積を求めるって、結局、積の公式じゃん」と気が付いたりします。「回帰式」や「共分散」についてはいずれ説明することとして、難しく感じられる手法も、結局はこういう基本的な計算(やはり四則演算です!)の積み重ねなのです。
とはいえ、ある程度の慣れは必要なので、軽く練習問題をこなしておきましょう(※スキップしたい場合は、3ページ目にジャンプしてください)。
練習問題
解答例
「因数分解と式の展開」練習問題の解答例は次の2ページ目に示します。3ページ目からは「添え字の利用」と「文字式の応用例(距離の総和の最小値の求め方)」について説明します。
Copyright© Digital Advantage Corp. All Rights Reserved.


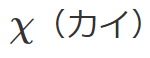
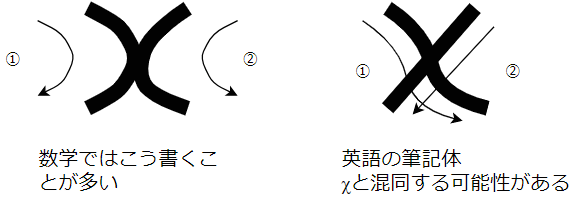 図1 xの書き方
図1 xの書き方
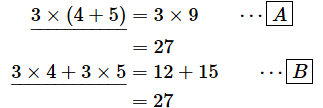
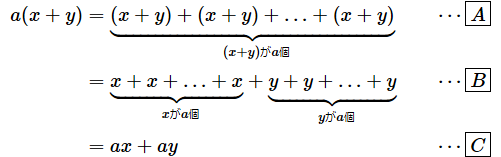
 図2 展開と因数分解
図2 展開と因数分解




