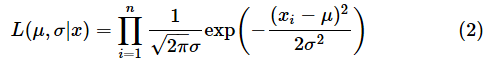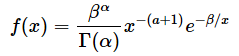[データ分析]ベイズ統計の確信区間 〜 バスケの勝利チームは何点取るのか?【番外編】:やさしい推測統計(区間推定編)
データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載(区間推定編)の第4回。今回は本編のお話から少し離れ、ベイズ統計の確信区間について、その考え方と求め方を解説します。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
連載:
この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』シリーズの「記述統計と回帰分析編」「確率分布編」に続く「推測統計(区間推定編)」です。
この連載では、観測されたデータを基に、母集団の母数について区間推定を行う方法を説明します。身近に使える表計算ソフト(Microsoft ExcelやGoogleスプレッドシート)を使いながら具体的に事例を見ていきます。
必要に応じて、Pythonのプログラムなどでの作成例にも触れることにしますが、数学などの前提知識は特に問いません。肩の力を抜いてぜひとも気楽に読み進めてください。
筆者紹介: IT系ライターの傍ら、非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。健康のために始めたウォーキングの友として、歩数によって経験値やアイテムが獲得できるゲームを始めるも、自宅でできるバトルに夢中になりすぎてむしろインドア化に拍車がかかった感も。最近、欲しいと思っているものは柔軟な身体と鋼のメンタル。大切だと思っていることは車間距離。
データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の推測統計(区間推定編)、第4回です。第2回は区間推定の第一歩として、正規母集団の母平均の区間推定に、第3回は正規母集団の母分散の区間推定に取り組み、それぞれの信頼区間を求めました。今回は頻度主義の信頼区間とベイズ主義の確信区間の違いとベイズ統計学での確信区間の求め方を見ていきます。
頻度主義の信頼区間とベイズ主義の確信区間の違いとは
前回までで見てきた区間推定とは、頻度主義と呼ばれる従来の統計学での考え方に従って、母平均や母分散などの母数を推定することでした(頻度主義やベイズ主義の意味については後述します)。信頼区間の意味は「例えば、信頼区間を何回も求めたとき、その試行の100(1−α)%の回に母数が含まれている」ということでした。αは有意水準と呼ばれ、0.05などの値がよく使われます。
ベイズ主義でも、ある程度の幅を持たせて母平均や母分散などの母数を区間推定することができます。その幅のことを確信区間または信用区間と呼びます(図1)。
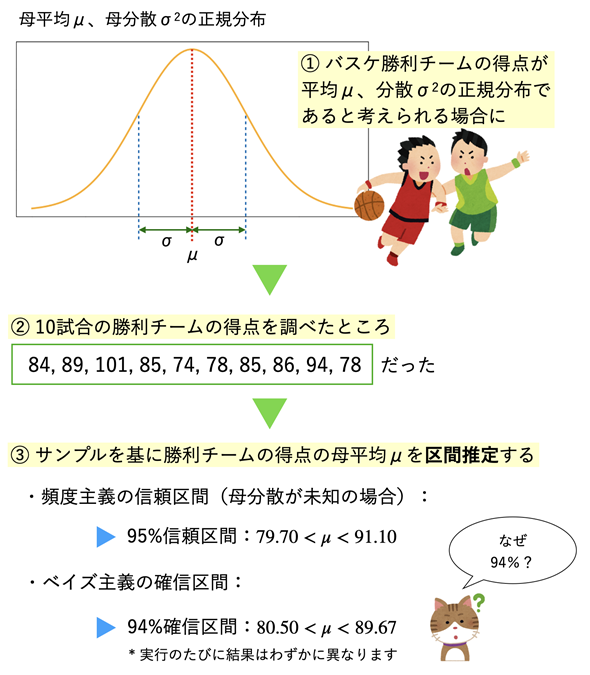 図1 母平均の信頼区間と確信区間
図1 母平均の信頼区間と確信区間母集団が正規分布するという前提の下、母集団から取り出されたサンプルを基に母平均を区間推定する。頻度主義の統計学とベイズ統計学では母数についての考え方が異なるので、計算の方法や結果も違ってくる。
図1で、ベイズ主義の確信区間が94%確信区間となっていますが、これは頻度主義の信頼区間とは異なるものだということを強調するために、あえて94%という値を使う(ことがよくある)ということです。もちろん、95%確信区間を求めることもできます(後述します)。
図1のデータは架空のデータですが、Bリーグの試合結果を参考にして作成したものです。ちなみに、Bリーグの成績などはこちらで参照できます。ここでは、母集団が正規分布に従っているという前提でお話を進めます(実は、シャピロ・ウィルク検定と呼ばれる方法で「正規分布でないとはいえない」(ただし、正規分布であるとは断言できません)という結果を求めてはいます。が、そのお話はまた仮説検定編で。
さて、頻度主義とベイズ主義の違いですね。端的に言うと、頻度主義では平均や分散などの母数が何らかの決まった値(定数)であると考えます。そもそも「頻度」主義と呼ばれるのは、試行の頻度を増やしていけば、測定値から得られた平均などの統計量が、定数である真の値に近づくという考え方だからです。母数は毎回求めたそれぞれの信頼区間に含まれる/含まれないのいずれかなので、(試行の頻度を増やせば)信頼区間に母数が含まれていた試行がどの程度あるかが求められる、と考えるわけです。「何%信頼区間とは、信頼区間を何度も求めたとき、その何%の回に母数が含まれているか」という回りくどい言い方をするのはそのためです。
一方のベイズ主義では、母数を変数(確率変数)と見なします。ベイズ主義では、ベイズの定理に基づいて、事前分布を更新して事後分布を求めます。何らかのデータ(証拠)が得られれば、そのデータに基づいて母数と考えられる値(仮説)を修正していく、という考え方です。母数を確率変数と見なして確率分布(事後分布)を求めるので、母数が何%の確率で確信区間に含まれるか、と素直に解釈できます。
ベイズ統計学での確信区間を求めてみる
ベイズ統計を理解するためには、条件付き確率の公式からベイズの定理を導き、それを確率分布に拡張する、といった順に説明されることが多いと思います。しかし、ここではそういった説明は全て割愛します。以下の式の意味だけを理解していれば、(パソコンを使って)計算できると思います。
「∝」は「比例する」という意味です。この式では、尤度(ゆうど)の意味が難しそうですね。尤度は「xというデータが得られたとき、母数がある値である尤もらしさ(もっともらしさ)がどの程度か」を表す関数(尤度関数)の値です。例えば、正規分布の場合、尤度関数Lは以下の式で表されます(が、この式は覚えなくても全く問題ありません。単に一例を示しただけです)。
左辺のLは尤度(likelihood)の頭文字です。引数に指定した(μ, σ|x)はxが与えられたときのμとσについての関数であるという意味です。
一方、右辺のΠは全ての積を求める、という意味です。……と、小難しいことを言いましたが、実際のところ、ある1つのxの値に対する尤度は、そのxの値に対する確率密度関数の値と一致します。ちなみに、この尤度関数の値が最大になるのはμの値がサンプル(幾つかのx)の平均と一致するときです。やっぱり小難しいですね。難しいと感じたらここは読み飛ばしても大丈夫です。
事前分布は、あらかじめ想定されている分布です。バスケの例で言えば「たぶん、平均は85点ぐらいで、標準偏差は8点ぐらいだろう」と(主観的に)考えられる分布です。実際に得られたデータを基に、事前分布を事後分布に更新して、妥当だと考えられる母数を推定するというわけです。データ量が多くなれば、最初に考えた主観的な値の影響は小さくなります。
ベイズ統計により母平均を区間推定してみよう
(1)式に基づいて事後分布を求めれば、母数の推定ができます。しかし、「∝(比例する)」というのをどう扱っていいか分かりませんね。事後分布の累積確率が全体で1になるように調整(正規化)すればいいのですが、その計算がやっかいになることがあります。
事前分布と事後分布が同じ形の分布の場合は解析的に(数式の計算で)求めることができるのですが、そうでない場合には乱数を使ったシミュレーションなどを利用するのが一般的です。そうすれば、得られたシミュレーションの結果から平均や分散などの母数が求められます。
例えば、マルコフ連鎖モンテカルロ法の手法のうちの一つであるメトロポリス法では、事前分布に従う乱数を取り出し(サンプリングし)、その値に尤度を掛けた値を求めます。そのようにして得られた直前の値と現在の値を基に、取り出したサンプルの値を事後分布の値として受け入れるかどうかを決めます。このようにして、次々とサンプルを取り出していけば、事後分布が得られるというわけです。ここでは、サンプリングの手法についてこれ以上は触れませんが、メトロポリス法の簡単な例(標準正規分布に従うデータのサンプリング)については、こちらをご参照ください。
なお、ベイズ更新によって求めた事後分布が事前分布と同じ形の分布になる場合、その事前分布のことを共役(きょうやく)事前分布と呼びます。以下の表のようなものがあります。
| 尤度関数 | 共役事前分布 | 事後分布 |
|---|---|---|
| 二項分布 | ベータ分布 | ベータ分布 |
| ポアソン分布 | ガンマ分布 | ガンマ分布 |
| 正規分布(母平均) | 正規分布 | 正規分布 |
| 正規分布(母分散) | 逆ガンマ分布 | 逆ガンマ分布 |
事後分布が事前分布と同じ形になるので、事後分布の欄は自明だが、同じ形の分布であることを強調するために掲載した。逆ガンマ分布は前連載の確率分布編でも紹介していなかった分布だが、これについては後のコラムでまとめる。二項分布、ポアソン分布、正規分布、ガンマ分布、ベータ分布は確率分布編で紹介しているので、必要に応じて参照してほしい。
では、最初の図1で示した母平均の区間推定を行ってみましょう。母平均をベイズ推定する場合は共役事前分布を使って解析的に計算することもできますが、ここでは、事後分布をシミュレーションによって求めてみます。ただ、Excelではかなり面倒になるので、今回はPythonのプログラムを使うことにします。そのためにはPyMCと呼ばれるモジュールが便利です。
PyMCは、マルコフ連鎖モンテカルロ法を利用してベイズ推定などを簡単に行うために使われるモジュールです。ただし、PyMCでは、上で簡単に解説したメトロポリス法ではなく、NUTSと呼ばれる効率的なアルゴリズムでサンプリングを行うのが標準になっています。コードについては詳しく解説しませんが、コード中のコメントとコードの下のキャプションを見れば、だいたいの意味は分かると思います(リスト1)。
サンプルプログラムはこちらから参照できます。リンクをクリックすれば、ブラウザが起動し、Google Colaboratoryの画面が表示されます(Googleアカウントでのログインが必要です)。最初のコードセルをクリックし、[Shift]+[Enter]キーを押してコードを実行してみてください。
import numpy as np
import pymc as pm # mcmcを利用するため
import arviz as az # 結果を可視化するため
# サンプルデータ
data = [84, 89, 101, 85, 74, 78, 85, 86, 94, 78]
with pm.Model() as model:
# 信頼区間と比較するために、標準偏差として不偏標準偏差を使う
sigma = np.std(data, ddof=1)
# 平均の事前分布を正規分布とする
mu = pm.Normal('mu', mu=85, sigma=sigma) # 事前分布の平均として85点を想定
# データの尤度を正規分布とする
obs = pm.Normal('obs', mu=mu, sigma=sigma, observed=data)
# MCMCサンプリングを実行
trace = pm.sample(2000, tune=1000, chains=4)
# 事後分布を要約する(94%確信区間を計算)
az.summary(trace)
PyMCを利用するには、pymcモジュールをインポートする。ここでは、そのモジュールのNormalクラスを使って事前分布を定義し、その下にあるNormalクラスのobserved引数に観測データ(data)を指定して尤度関数を定義している。どちらも、Normalクラスの最初の引数には、変数を識別するために付ける名前(実行結果にも表示される)を指定している。その後の引数(muやsigma)で母数などを指定する。続くsample関数でサンプリングが行われ、事後分布が求められる。arvisモジュールはサンプリングの結果を可視化するために使われる。summary関数によって点推定や区間推定の値が表示される。
PyMCでは、sample関数によって、尤度と事前分布を基にサンプリングを行い、事後分布を求めます。リスト1の例ではサンプルの個数は2000個です。sample関数の引数tuneで指定した1000という値は、サンプルの生成が安定するまでの最初の1000個のサンプルは捨てるという指定なので、合計で3000個のサンプルが作成され、最初の1000個が捨てられるというわけです。chainsの指定はこのようなサンプリングを何回行うかという指定です。異なる初期値から4回のサンプリングを行うことにより、ほぼ同じ結果に収束したかどうかを判定します。従って、この例では、事後分布の母数を推定するために2000×4=8000個のサンプルが利用されることになります。
結果は図2のようになります。ただし、乱数を使うので、実行のたびにわずかに値は異なります。なお、95%確信区間を求めたいときは、コードの最後の行をaz.summary(trace, hdi_prob=0.95)とします。
 図2 ベイズ推定によって求めた母平均の確信区間
図2 ベイズ推定によって求めた母平均の確信区間hdi_3%の値(80.496)から、hdi_97%の値(89.668)までが94%確信区間。mcse_meanは事後分布の平均のモンテカルロ標準誤差。mcse_sdは事後分布の標準偏差のモンテカルロ標準誤差。いずれも値が小さい方がよく推定できているということ。ess_bulkやess_tailは独立したサンプルが採れているかどうかを計る指標。サンプリングがうまくできていれば、いずれの値も大きくなる(おおむね500以上)。r_hatは十分に収束しているかどうかを表す値。1.0であれば収束している。
図2に表示されているhdiは、high density interval(最高密度区間)の略です。頻度主義の信頼区間では、例えば累積確率の左右2.5%を除外した95%の範囲を95%信頼区間としていましたが、PyMCではhdiを使うのが一般的です。hdiでは確率密度の高い94%の範囲を確信区間とします。信頼区間では確率密度関数を縦に切るのに対して、hdiでは横に切るといったイメージです(図3)。
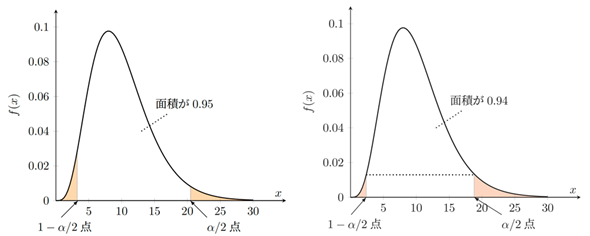 図3 信頼区間(左)と最高密度区間(右)の違い
図3 信頼区間(左)と最高密度区間(右)の違いこれらのグラフは自由度10のカイ二乗分布での例。正規分布やt分布などの左右対称な分布では、信頼区間と最高密度区間がほぼ等しくなるので、あえて左右対称でない例を掲載した。95%と94%の違いは上で述べた通りなので気にしなくてもよい。それよりも、考え方の違いを確認しよう。信頼区間は左右の2.5%を除外した95%の範囲となるが、確信区間(最高密度区間)では、確率密度関数の値の最も高い位置から94%の範囲となる。
頻度主義の区間推定については、第1回と第2回でExcelを使って計算したので、あらためて説明はしませんが、比較できるようにPythonのプログラムを作成しておきました。サンプルファイルの2つ目のセルに入力してあります(リスト2)。
import numpy as np
from scipy import stats
# サンプルデータ
data = [84, 89, 101, 85, 74, 78, 85, 86, 94, 78]
# 標本平均
s_mean = np.mean(data)
# 不偏標準偏差
s_std = np.std(data, ddof=1)
# 標本サイズ
n = len(data)
# 信頼係数
confidence_level = 0.95
# t分布の2.5%点
lower, upper = stats.t.interval(0.95, df=9) # 信頼区間の計算
# 信頼区間の表示
print(s_mean + lower, s_mean + upper)
# 出力例:83.13784283714591 87.6621571628541
scipyのstats.t.interval関数により、自由度df=9の95%信頼区間を求める。この関数は右側確率が97.5%となる下限のt値(負の値)と2.5%となる上限のt値(正の値)をタプルとしてまとめて返すので、それぞれの値(lowerやupper)をサンプルの平均(s_mean)に足せば信頼区間が求められる。
コラム 逆ガンマ分布を利用し、標準偏差と平均の区間推定を同時に行う
リスト1では、事前分布の標準偏差として不偏標準偏差を指定しましたが、母標準偏差(母分散)も同時にベイズ推定することができます。このとき、標準偏差の事前分布として切断正規分布(半正規分布)を使ったり、分散の事前分布として共役事前分布である逆ガンマ分布を使ったりするのが一般的です。
切断正規分布とは正規分布の一部を切り取ったものです。標準偏差は0以上なので、正規分布の0以上の部分を使います。その場合は、サンプルコード中の
sigma = np.std(data, ddof=1)
の代わりに、例えば、
sigma = pm.HalfNormal('sigma', 8) # 事前分布の標準偏差として8を想定
と記述すれば、標準偏差と平均のベイズ推定ができます。pymcモジュールのHalfNormalクラスは台が0〜∞の切断正規分布です。サンプルファイルの3つ目のセルには切断正規分布を利用したコードを含めてあるので、興味のある方はご参照ください。
一方の逆ガンマ分布とは、ガンマ分布に従う確率変数の逆数の分布で、台は0〜∞です。逆ガンマ分布の確率密度関数f(x)は以下の式で表されます。母数はαとβです。
図4は幾つかのα, βを指定して、逆ガンマ分布の確率密度関数を描いたものです。
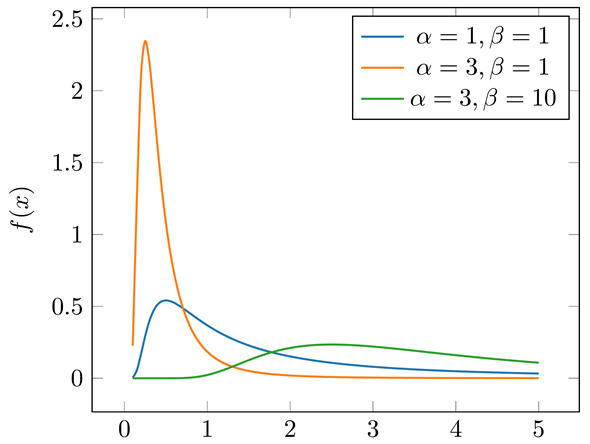 図4 逆ガンマ分布の確率密度関数
図4 逆ガンマ分布の確率密度関数逆ガンマ分布はαが大きくなると山が高く、左に寄る形になり(α=3,β=1のオレンジ色のグラフ)、βが大きくなると幅が広がる(α=3,β=10の緑色のグラフ)。従って、事前の情報をあまり入れたくない場合はαを小さく、βを大きくするとよい。
ガンマ分布に従う確率変数をτ(タウ)とし、ガンマ分布をGammaとすると、
と表せます。この確率変数τの逆数が逆ガンマ分布に従うということなので、逆ガンマ分布をInvGammaとすると、
となるわけです。従って、逆ガンマ分布を利用して標準偏差の区間推定を行いたい場合には、事前分布として(分散の推定に利用される)逆ガンマ分布のルートを指定します。例えば、サンプルコード中の
sigma = np.std(data, ddof=1)
の代わりに、
tau = pm.Gamma('tau', alpha=1, beta=64) # 逆ガンマ分布のパラメータ
sigma = pm.Deterministic('sigma', 1 / np.sqrt(tau)) # 標準偏差
と書けば、標準偏差と平均のベイズ推定ができます。Deterministic関数は事前分布のパラメーターではない変数についても値を求めるための指定です(逆ガンマ分布のパラメーターはαとβで、標準偏差はそれらを基に求められる値です)。
サンプルファイルの4つ目のセルには逆ガンマ分布を利用したコードが入力されています。興味のある方はご参照ください。
今回は番外編として、ベイズ統計における区間推定について、基本的な考え方から確信区間の計算方法までを解説しました。
次回からはまた頻度主義の考え方での区間推定について解説する予定です。次回は母平均の差についての区間推定を見ていきます。お楽しみに!
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ


 羽山博
羽山博