[評価関数]平均二乗パーセント誤差の平方根(RMSPE:Root Mean Squared Percentage Error)とは?:AI・機械学習の用語辞典
用語「平均二乗パーセント誤差の平方根」について説明。評価関数の一つで、各データに対して「予測値と正解値との差を、正解値で割った値(=パーセント誤差)」の二乗値を計算し、その総和をデータ数で割った値(=平均値)に対する平方根の値を表す。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
用語解説「RMSPE」
機械学習における平均二乗パーセント誤差の平方根(RMSPE:Root Mean Squared Percentage Error)とは、名前の通り、平均二乗パーセント誤差(MSPE、後述)の平方根 √(ルート:Root)の値を出力する関数である。(図1)。
平均二乗パーセント誤差(MSPE)とは、各データに対して「予測値と正解値との差を、正解値で割った値(=パーセント誤差)」の二乗値を計算し、その総和をデータ数で割った値(=平均値)を出力する関数である(※2021/06/23修正:「100」を掛けていましたが誤りでした。お詫びして訂正さていただきます)。なお誤差は、「予測値−正解値」ではなく「正解値−予測値」でもよい。
定義と数式
「パーセント誤差の二乗値」がイメージしやすいように、簡単なデータで手計算してみよう(図2)。
図2のデータでは5個(例えば1時〜5時)の期間からなる時系列データがあり、予測値−正解値で「誤差」を計算し、(誤差÷正解値)の二乗値で「二乗パーセント誤差」を計算している。5個の計算結果を平均し、最終的に0.1507という平均二乗パーセント誤差の平方根(RMSPE)が計算されている。
用途
類似の評価指標にMAPE(Mean Absolute Percentage Error:平均絶対パーセント誤差)がある。MAPEが絶対値を使うのに対し、RMSPEは二乗した計算結果の平方根を取るという違いがある。RMSPEは、「パーセント誤差」で評価したいが、MAPEのように絶対値を使いたくない場合に、評価関数として採用できるだろう。
どちらも基本的な用途や利点/欠点は同じであるため、本稿での説明は割愛する。MAPEに記述した用途の解説を参考にしてほしい。
API
scikit-learnやTensorFlow(2.x)/Keras、PyTorchといった主要ライブラリでRMSPEは、標準では用意されていない。カスタムで自作する必要がある。
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ

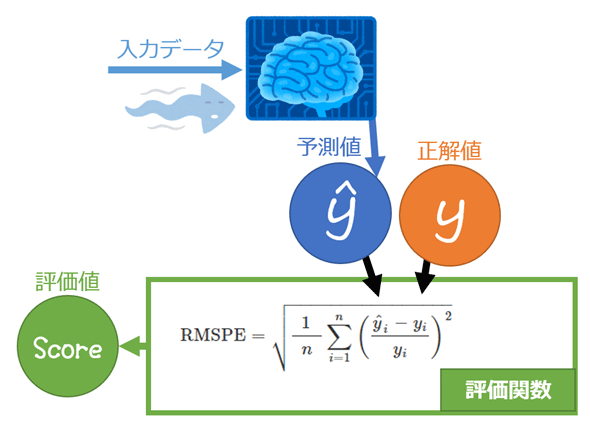

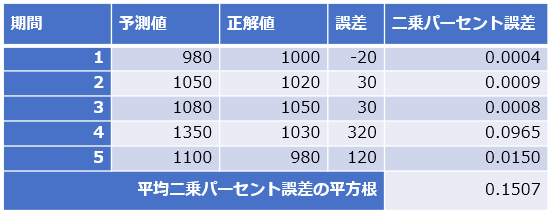 図2 平均二乗パーセント誤差の平方根(RMSPE)の計算例
図2 平均二乗パーセント誤差の平方根(RMSPE)の計算例



