[損失関数/評価関数]平均二乗対数誤差(MSLE:Mean Squared Logarithmic Error)/RMSLE(MSLEの平方根)とは?:AI・機械学習の用語辞典
用語「平均二乗対数誤差」について説明。損失関数/評価関数の一つで、各データに対して「予測値の対数と正解値の対数との差(=対数誤差)」の二乗値を計算し、その総和をデータ数で割った値(=平均値)を表す。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
用語解説「MSLE」
機械学習における平均二乗対数誤差(MSLE:Mean Squared Logarithmic Error)とは、各データに対して「予測値の対数と正解値の対数との差(=対数誤差)」の二乗値を計算し、その総和をデータ数で割った値(=平均値)を出力する関数である。(図1)。なお対数誤差は、「予測値の対数−正解値の対数」ではなく「正解値の対数−予測値の対数」でもよい。
定義と数式
数式では、log(1+ŷi)やlog(1+yi)という形で「+1」していることに注意してほしい。もし「+1」せずにlog(ŷi)やlog(yi)にした場合、ŷiやyiの値が0だと、その自然対数(eを底とする対数)を計算する式は「log(0)=マイナス無限大」となってしまい、数値が計算できなくなる。これを回避するためにわざと「+1」しているのである(図2)。
また「+1」することの利点として、log(1+ŷi)やlog(1+yi)という式のŷiやyiの値が0だと、「log(1)=0」という結果となり、図2のように座標(0,0)を通るので分かりやすくなることが挙げられる。なお、正解値や予測値は-1より大きい必要がある。
用途
MSLEは、主に回帰問題における出力層の評価関数としても用いられる。また、損失関数として使われることもある。いずれの関数から出力される値も、0に近いほどより良い。数学では底が同じ対数同士の引き算は割り算に変形できることに着目すると(※数学入門連載の対数編のポイント2を参照)、MSLEは「予測値/正解値」の比率に着目した指標だと見なすことができる。
MSLEと似ている平均二乗誤差(MSE:Mean Squared Error)という関数の欠点は、誤差が大きいほど過大に評価するため、外れ値に敏感であることだった。それに対して対数の誤差を使うMSLEは、前掲の図2を見ても分かるように対数の性質上、誤差が大きくなっても過大に評価しない。つまりMSLEは、誤差が極端に大きい場合にも対応できるという利点がある。
またMSLEは、その対数の性質上、正解値と比較して予測値が大きい場合よりも小さい場合の方が大きなペナルティーを課す。例えば正解値が1000の場合を考えてみよう。それと比較して、
- 予測値が1500と大きい場合の対数誤差の二乗は0.164
- 予測値が500と小さい場合の対数誤差の二乗は0.479
となる。どちらも正解値1000からの差は500なのに、予測値が小さい場合の方が大きな評価値となっていることに注目してほしい。このような特性により下振れを抑える効果があることも、MSEにするかRMSEにするかの使い分け指針となるだろう。
ただしMSLEにはMSEと同じ欠点がある。具体的にはMSLEは、対数誤差を二乗することで単位が変わってしまうので、人間にとって単純には理解しづらいという問題がある。この単位問題を回避するためには、ルート(√)を使って二乗した単位を元の単位に戻す方法(後述のRMSLE:Root MSLE)などが考えられる。
API
主要ライブラリでMSLEは、次のクラス/関数で定義されている。
- scikit-learn: mean_squared_log_error関数
- TensorFlow(2.x)/Keras: MeanSquaredLogarithmicErrorクラスやmean_squared_logarithmic_error()関数、また(compile()メソッドの引数metricsで)'mean_squared_logarithmic_error'や'MSLE'など
- PyTorch: ※標準では用意されていない。カスタムで自作することは可能
用語解説「RMSLE」
RMSLE(Root MSLE:MSLEの平方根)とは、名前の通り、MSLEの結果に対するルート(√)を求めることである。MSLEで二乗した単位が元に戻るので、MSLEよりも人間が理解しやすい指標だといえる。
定義と数式
API
主要ライブラリのscikit-learnやTensorFlow(2.x)/Keras、PyTorchでは、RMSLEは標準実装されていない。必要に応じて、カスタム実装などをする必要がある。
Copyright© Digital Advantage Corp. All Rights Reserved.

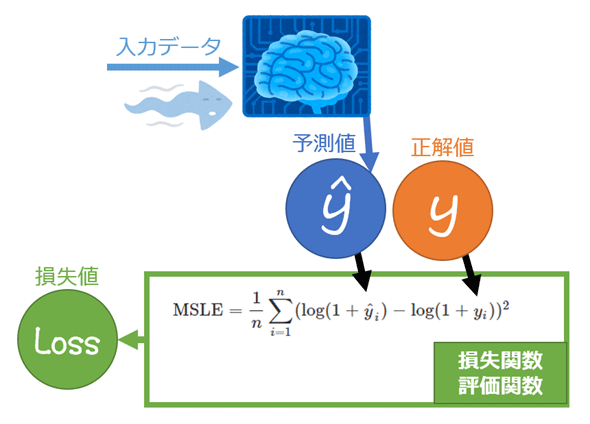

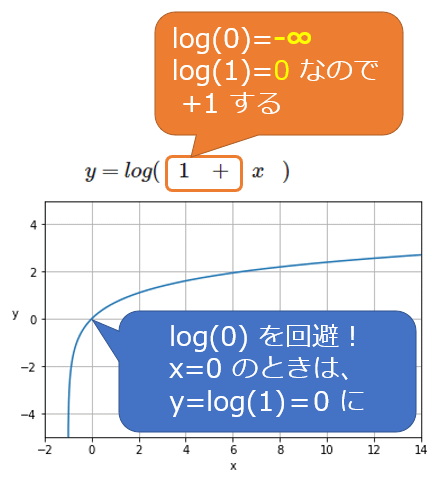 図2 y=log(1+x)の自然対数グラフ
図2 y=log(1+x)の自然対数グラフ




