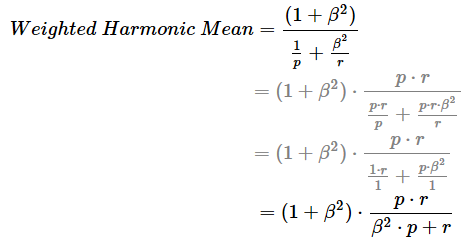［評価指標］重み付きF値（Weighted F-measure）／Fβスコア（Fβ-score）とは？：AI・機械学習の用語辞典
用語「重み付きF値」、別名：「Fβスコア」について説明。二値分類タスク（問題）に対する評価指標の一つで、適合率と再現率のトレードオフ関係に着目し、2つの値を重み付き調和平均「（1＋β二乗）×（適合率×再現率）÷（β二乗×適合率＋再現率）」した値を指す。
用語解説
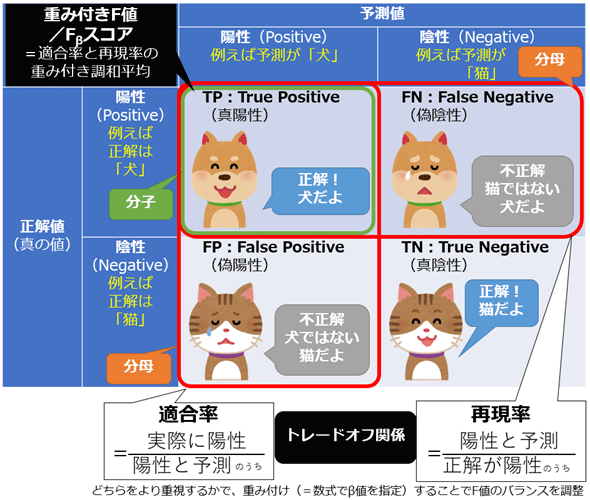
統計学／機械学習における重み付きF値（Weighted F-measure）とは、（基本的に）二値分類のタスク（問題）に対する評価指標の一つで、適合率（Precision）と再現率（Recall）のトレードオフ関係に着目し、2つの値を重み付き調和平均（詳細後述）した値のことである（図1）。0.0（＝0％）〜1.0（＝100％）の範囲の値になり、1.0に近づくほどより良い。
名前から分かるように重み付きF値は、F値／F1スコアに重みを付ける派生バージョンである。F値は、調和平均を用いることで適合率と再現率のバランスを同等に重視して平均する。しかし「どちらかをより重視したい」というニーズもあるだろう。重み付きF値は、適合率または再現率のどちらかに重みを付けてバランスをどちかに傾けて平均する（重みの付け方は後述する）。つまり1.0に近いことは、「指定した重みにおいて、最も効率よく適合率と再現率のバランスが取れた機械学習モデル」と言える。
重み付きF値の計算は、（1＋β2）×適合率×再現率をβ2×適合率＋再現率で割ることで計算できる。この数式にあるβとは、「再現率（Recall）をどれだけ重視するか」を意味する重み付けの値である。
重み付き調和平均（Weighted Harmonic Mean）とは、F値／F1スコアで解説した調和平均の応用バージョンである。例えばpとrという2つの“率”（＝2つの値の比、つまり分子／分母で構成された指標において、その分子を基準とする場合）の重み付き調和平均を算出する式は以下のようになる（※なお、pの方には暗黙的に12の重みを掛けているものと見なしてほしい）。
F値と同様の例題を挙げておこう。重みの意味は後述するが、ここではβ＝2.0を指定してみる（＝rを2倍重視するといったイメージになる）。この場合、p＝時速40kmとr＝時速60kmでの重み付き調和平均値は、（1＋22）×（40×60）／（22×40＋60）＝（5）×（2400）／（220）＝約54.5となり、平均時速54.5kmが答えである。参考までに調和平均だと平均時速48kmと算出されるので、この重み付き調和平均の計算では、よりrが重視されたことが分かる。逆に例えばβ＝0.5（1.0未満の値）を指定すると平均時速42.9kmが求まるので、rが軽視され、pがより重視されたことが分かる。
重み付き調和平均の計算式におけるpをPrecision（適合率）、rをRecall（再現率）と置くと、下記の計算式になる。TP／FP／FNの意味は、図1や混同行列の用語解説を参考にしてほしい。
この重み付き調和平均による計算値は、Fβスコア（Fβ-score）とも呼ばれる。βには以下のような値を指定できる。
- β＝0.0： 適合率しか見ない
- 0.0＜β＜1.0： 指定した比率で、適合率（Precision）をより重視する
- β＝1.0： 適合率と再現率を同等に扱う（＝F1スコアと同じ結果）
- 1.0＜β＜∞： 指定した倍数で、再現率（Recall）をより重視する
β値を実際にどのような値にするかは試行錯誤が必要になるが、イメージしやすい目安として、例えば再現率が2倍ほど重要な場合には、まずはβに2.0などを指定してみるとよいだろう（F2スコア）。また目安として、適合率を50％ほど再現率よりも重視したい場合には、まずはβに0.5（＝1.0−0.5）などを指定してみるとよいだろう（F0.5スコア）。
Copyright© Digital Advantage Corp. All Rights Reserved.
ITmediaはアイティメディア株式会社の登録商標です。