［評価指標］mAP（mean Average Precision）とは？：AI・機械学習の用語辞典

用語「mAP」について説明。多クラス分類タスク（問題）に対する評価指標の一つで、各クラスのAP（Average Precision：平均適合率）を平均した値を意味し、mAP値が1.0に近いほど分類を予測する機械学習モデルの性能が高い。物体検知の評価指標としてよく使われている。

[一色政彦，デジタルアドバンテージ]

連載目次

用語解説

　統計学／機械学習におけるmAP（mean Average Precision）とは、（基本的に）多クラス分類のタスク（問題）に対する評価指標の一つで、各クラスのAP（Average Precision：平均適合率）を平均した値を指す。0.0（＝0％）〜1.0（＝100％）の範囲の値になり、1.0に近づくほどより良い。特に物体検出の評価指標としてよく使われている。

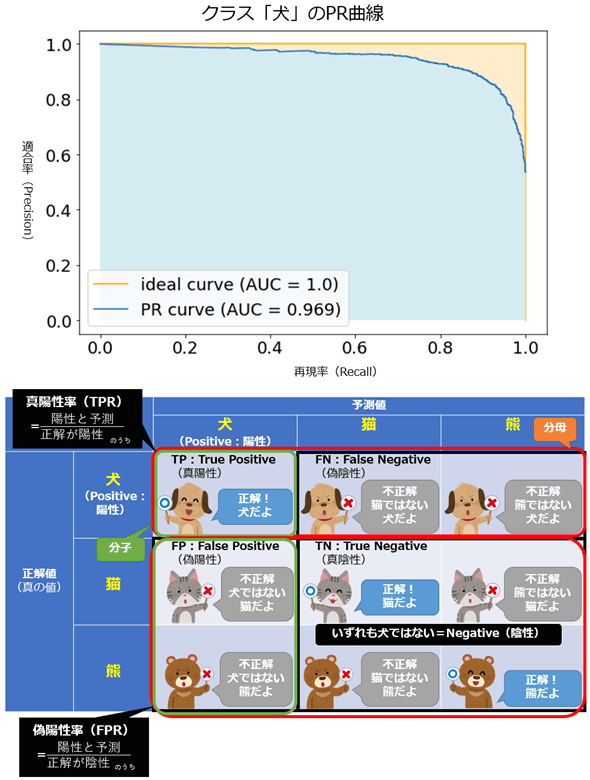
　AP（平均適合率）はPR曲線を要約した値を表す（参考：「PR-AUC／AP」の用語解説）。PR曲線（Precision-Recall Curve、適合率-再現率の曲線）とは、縦軸に適合率（Precision）、横軸に再現率（Recall）を取ってプロットした場合の曲線、つまり適合率と再現率の関係を表現したグラフのことである（図1）。多クラス分類の場合は、クラスごとにPR曲線を描く必要がある（多クラスでの適合率と再現率と求め方は、「多クラス分類の混同行列」の用語解説を参考にしてほしい）。

図1　「PR曲線」と「mAP」のイメージ

　PR-AUC（PR曲線を使ったAUC、別名：AUPRC）とAP（平均適合率）は同じPR曲線を評価する指標である。が、計算アプローチが（基本的に）異なる。AUCでは、台形法（trapezoidal rule：台形公式）という手法で定積分を近似計算することが一般的であるのに対し、APではしきい値ごとの適合率（Precision）を加重平均することが一般的だ。よって両者は必ずしも同じ計算結果とならないので注意してほしい。

　APの計算方法を数式で表現すると、以下のようになる。

　しきい値（閾値）については「AUC」の用語解説を参考にしてほしい。R_iは、i番目のしきい値における再現率（Recall）の値を指す。R_i−1は、i−1番目、つまりi番目の1つ前のしきい値における再現率の値を意味する。P_iは、i番目のしきい値における適合率（Precision）の値を指す。

　「今のしきい値の再現率（R_i）」から「前のしきい値の再現率（R_i-1）」を引くことで、再現率の増加分を計算している。これが加重平均における「重み」となる。この重みを、今のしきい値における適合率に掛け、その計算結果を全しきい値の総数分、足し合わせることで、加重平均の計算が実現されている。この計算のため「平均」適合率と呼ばれる。

　mAPは、このように計算した各クラスのAPを平均するだけである。計算式は以下のようになる。

「AI・機械学習の用語辞典」