［評価指標］AUC（Area Under the ROC Curve：ROC曲線の下の面積）とは？：AI・機械学習の用語辞典

用語「AUC」について説明。二値分類タスク（問題）に対する評価指標の一つで、「ROC曲線の下の面積」を意味し、AUC値が1.0に近いほど分類を予測する機械学習モデルの性能が高い。

» 2023年12月04日 05時00分公開

[一色政彦，デジタルアドバンテージ]

用語解説

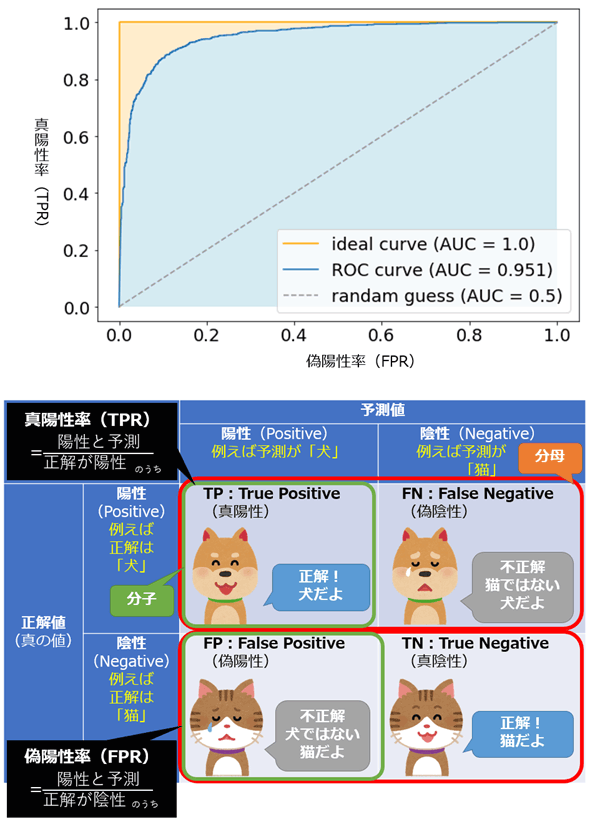
　統計学／機械学習におけるAUC（Area Under the ROC Curve、AUROC、ROC-AUC）とは、主に二値分類タスク（問題）に対する評価指標の一つで、「ROC曲線（後述）の下の面積」を意味する。この指標は、0.0（＝0％）～1.0（＝100％）の範囲の値を取り、1.0に近いほどモデルの予測性能が高いことを示す。

　例えば機械学習モデルによる予測が全て正解（＝図1のideal curve：理想の曲線）であった場合、AUC値は1.0となり、予測性能が高いことを意味する。AUC値が0.5の場合は、機械学習モデルによる予測がランダムな推測（randam guess＝当てずっぽうの予測）と同等であることを示し、予測性能が低いことを意味する。AUC値の基準は次のようになる。

0.9～1.0：非常によい（excellent）
0.8～0.9：よい（good）
0.7～0.8：まあまあ（fair）
0.6～0.7：よくない（poor）
0.5～0.6：失敗（fail）

　なおAUCには、下記の2種類がある。

ROC曲線を使ったAUC（本稿で解説）
PR曲線を使ったAUC（別稿で解説）

　単に「AUC」と言う場合、「ROC曲線を使ったAUC」を指すことが多い。

　ROC曲線（Receiver Operating Characteristics Curve、受信者操作特性曲線）とは、縦軸に真陽性率（TPR：True Positive Rate）、横軸に偽陽性率（FPR：False Positive Rate）を取ってプロットした場合の曲線、つまりTPRとFPRの関係を表現したグラフのことである（図1）。

図1　「ROC曲線」と「AUC」のイメージ

　TPRは感度（Sensitivity）／再現率（Recall）と全く同じ式である。FPRは「1から特異度（Specificity）を引いた式」と同じ意味である。TPRとFPRの計算式は本稿の最後で示す。

　感度や特異度では分類判定のしきい値を指定したが、AUCのTPR／FPRでは0.0～1.0の範囲でしきい値（閾値：threshold value＝カットオフポイント：cutoff points）を細かく指定していくことで、図1のようなROC曲線が描ける。描き方の詳細は、「機械学習の評価関数（二値分類／多クラス分類用）を理解しよう」という記事におけるAUCの説明を参考にしてほしい。

　このように多数のしきい値を用いるので、ある特定のしきい値しか使わない正解率（Accuracy）やF₁スコアと比べて、AUCは「しきい値の影響を受けずに、より汎用的なモデル性能が計測できる」という特長がある。

　例えば貸金業で貸し倒れリスクを予測する、つまり「貸し倒れる／貸し倒れない」という二値分類を行うモデルであれば、「厳しく判定したい」「緩く判定したい」といった形で利用目的に応じてしきい値を変更することが考えられるだろう。この場合、しきい値の影響を考慮せずに、汎用的なモデルの性能の良さを計測したい。こういった場面では、正解率でもF₁スコアでもなく、AUCを使った方がよい。

　汎用的な性能の良さを計測できるAUCは、LogLossの説明で書いた通り、異なるデータセットを使った機械学習モデル間の性能を比較したい場合にも使いやすい評価指標である。

　このようなAUCだが、やはり欠点がある。AUCのTPRは正解値が陽性のものだけを対象にした値で、FPRは正解値が陰性のものだけを対象にした値である。陽性と陰性の正解値を持つデータの数が極端に不均衡（imbalanced data）な場合、その影響をもろに受けてしまう可能性がある。例えば正解値が陽性のデータ数が少なすぎる場合、TPRがFPRよりも個々のデータに敏感に反応するようになり、図1のようなきれいなグラフにならない可能性が高まる。よって「ROC曲線を使ったAUC」を評価指標として用いる場合には、教師ラベルの陽性と陰性はできるだけ同じくらいの数にそろえた方がよい。それができない場合は、「PR曲線を使ったAUC」を使うことを検討するとよい。

　感度（Sensitivity）の記事でも簡単に説明しているが、二値分類の混同行列を使ってあらためてTPRとFPRの計算式を書き出すと以下のようになる。