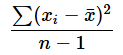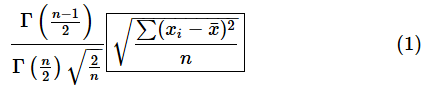やさしいデータ分析【推測統計編】 新連載開始!〜 推測統計って何? どう役に立つの?:やさしい推測統計(区間推定編)
初歩からステップアップしながら学んでいく『やさしいデータ分析』シリーズ第3弾。「記述統計と回帰分析編」「確率分布編」に続き、「推測統計(区間推定編)」がスタート。第1回は出発点として、推測統計の「点推定」と「区間推定」の意義や考え方を学びます。この機会に、データ分析の基礎をしっかり学んでみませんか?
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
連載:
この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』シリーズの「記述統計と回帰分析編」「確率分布編」に続く「推測統計(区間推定編)」です。
この連載では、観測されたデータを基に、母集団の母数について区間推定を行う方法を説明します。身近に使える表計算ソフト(Microsoft ExcelやGoogleスプレッドシート)を使いながら具体的に事例を見ていきます。
必要に応じて、Pythonのプログラムなどでの作成例にも触れることにしますが、数学などの前提知識は特に問いません。肩の力を抜いてぜひとも気楽に読み進めてください。
筆者紹介: IT系ライターの傍ら、非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。健康のために始めたウォーキングの友として、歩数によって経験値やアイテムが獲得できるゲームを始めるも、自宅でできるバトルに夢中になりすぎてむしろインドア化に拍車がかかった感も。最近、欲しいと思っているものは柔軟な身体と鋼のメンタル。大切だと思っていることは車間距離。
データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載『社会人1年生から学ぶ、やさしいデータ分析』のシリーズとして、「記述統計と回帰分析編」「確率分布編」に続いて、今回から「推測統計(区間推定編)」を開始します。2023年から始まった連載もおかげさまでいよいよ第3シーズンに突入です。
これからのお話は、「推測統計」と呼ばれる分野に関するものとなります。そこで、推測統計とは何かを簡単にお話ししておきましょう。実際のところ、具体的な例で学んでいった方が、実感を持って理解できるので、ここでは、簡単に概要を紹介するだけにとどめます。
推測推定とは 〜 区間推定と仮説検定の概要
推測統計には、大きく分けて「統計的推定(点推定・区間推定)」と「仮説検定」と呼ばれる方法があります。統計的推定では、母集団の分布の平均や分散などの母数(パラメーター)を推定します。この連載では、特に、区間推定を取り扱います。一方、仮説検定では「母平均が何らかの値と等しいか」などの仮説が支持されるかどうかを判断します。
実は、仮説が「支持されるかどうか」という表現にはやや語弊があります。仮説検定では、帰無仮説と呼ばれる仮説が棄却されるかどうかを判断します。帰無仮説が棄却されるならば、対立仮説を採用する、といった考え方を取ります。
これまでの2つの連載で学んだ内容と併せて、チャートにまとめておきましょう(図1)。
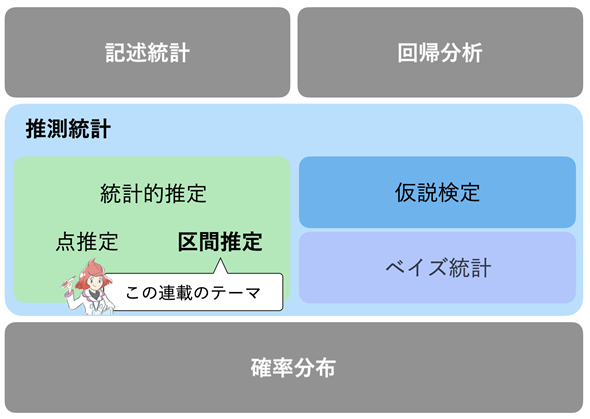 図1 この連載では区間推定を取り扱う
図1 この連載では区間推定を取り扱う白い字で書かれたものがこれまでの連載で学んできたもの。中でも前回の連載で見た確率分布は推測統計の基礎となる。
今回の連載では推測統計の中でも区間推定に焦点を当てる。なお、この連載の続編として「推測統計(仮説検定編)」や「ベイズ統計編」も予定している。
図1には、今回のテーマである区間推定の他に点推定も記してあります。それらの関係について見ていきましょう。
統計的推定って何をどう推定するの?
この連載では、推測統計のうち統計的推定(特に区間推定)を学びます。統計的推定というからには、統計的な方法によって、何かを基に、何かを推定するわけです。その「基になる何か」とは、母集団から取り出されたサンプル(標本)です。一方の「推測される何か」とは、母集団の分布の平均や分散などの母数(パラメーター)です。
問題となるのは推定のための「統計的な方法」ですね。そういうわけで、この連載では、区間推定を行うための統計的な方法の考え方と計算方法を解説していきます。
具体的な内容は次回以降の連載でのお話になりますが、大ざっぱに統計的推定の手順を図解しておきましょう(図2)。図の中には点推定や区間推定、信頼区間などの用語が記されていますが、それらの意味については後で説明します。
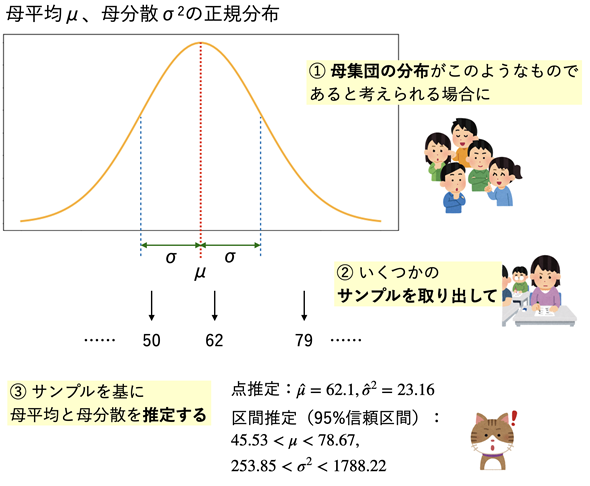
「母集団がどのような分布であるか」という前提の下、母集団から取り出されたサンプルを基に母数を推定する。推定には点推定と区間推定がある。「点推定:」にある
の上に付いている「^」は、推定値であるということを表すもの。図中の推定値は実際に点推定と区間推定を行った結果。その考え方や計算方法を知るのがこの連載の目的。
図2は、ある企業の中で無作為に選ばれた社員が英語の資格試験を受けたような状況を想定したものです。従って、母集団はその企業の社員全体です。サンプルは、そのうち資格試験を受験した人たちです。
母集団の分布の母数を推定するには、まず、大前提として、「母集団の分布がどのようなものであるか」が分かっている(あるいは仮定できる)必要があります。図2では、「母集団の分布が正規分布である」という前提の下で、母集団からサンプルを取り出して、測定値(資格試験の場合は点数)を求めています。そして、それらの測定値を基に母集団の平均や分散を推定するというわけです。
母集団とサンプルについては、少し慎重に考える必要があります。例えば、単に「英語の資格試験を受けた社員」がサンプルである場合、社員全体を母集団と考えるのは妥当ではありません。
なぜなら、英語の資格試験を受けた人は、英語を必要としている人(少なくともそういうモチベーションを持っている人や英語を勉強している人)たちなので、英語を必要としていない社員よりも試験の成績は良いと考えられます(実際にはそうではないかもしれませんが)。平たく言えば社員全体を代表しているわけではないということです。
図2では「無作為に抽出された」社員が受験しているので、社員全体を母集団と考えても問題はありません。当然のことながら、図2の例でビジネスパーソン全体や日本人全体を母集団と考えることはできません。
図中に記した推定値は実際に点推定と区間推定を行った結果です。この連載の目的は「どの分布のどの母数を区間推定するにはどのような計算を行えばいいのか」を身に付けることです。その前に、懸案事項を解決しておきましょう。点推定と区間推定がどのようなものであるかをお話しします。
点推定や区間推定って何を推定するの 〜 推測統計の応用に向けて
点推定
これまでの連載では、私たちは「平均が幾ら、不偏分散が幾ら」というように、母数の推定値を1つの数値で表してきました。このような推定の方法を点推定と呼びます。例えば、母集団が正規分布である場合、母平均の推定値は算術平均(相加平均)で求められます。また、母分散の推定値としては、各データから求めた不偏分散の値を使いました。念のため、不偏分散を求めるための式を掲載しておきます。
Excelを使えば、平均値はAVERAGE関数で、不偏分散はVAR.S関数で求められますね。すでにご存じの方も多いでしょうから、計算の方法を解説するまでもないでしょう……が、念のため後のコラムでまとめておくことにします。ここで重要なのは「区間推定」がどのようなものであるかということですね。それをお話しします。
区間推定
確率分布編でもお話ししたように、母数が決まれば、分布が一意に決まります。しかし、たった1つの母数の推定値だけで「母集団の分布はこうだ」と決め付けてしまうのはずいぶんと乱暴な気がしますね。そこで、もう少し幅を持たせて母数を推定しよう、というのが区間推定の基本的な考え方です。
前掲の図2では、区間推定の例として、母平均の95%信頼区間が45.53<μ<78.67、母分散の95%信頼区間が253.85<σ2<1788.22であるという結果を掲載しています。
今回は連載の概要と全体像、基本的な考え方の理解にとどめるので、これらの値をどのようにして計算するのかについては解説しません。もったいぶらずに早く話してよ、と思われるかもしれませんが、次回以降、一歩ずつゆっくりと進めていきます。
この結果を見ると「母平均は95%の確率で45.53〜78.67の間にある」とか「母分散は95%の確率で253.85〜1788.22の間にある」と言いたくなりますが、そういうことではありません。母平均や母分散などの母数は未知ではありますが、何らかの決まった値、つまり定数であると考えられます。母数は確率変数ではないので、母数がどの範囲にある確率は幾らと決められるものではないからです。
この考え方は、頻度主義と呼ばれるこれまでの統計学の考え方です。ベイズ統計の確信区間では、母数を変数と考えるので、「母数は何%の確率で幾ら〜幾らの間にある」と言えます。ベイズ統計の確信区間については、この連載でも少し触れることにします(この後に掲載した、「さまざまな区間推定 〜 この連載で取り扱う内容」の表1を参照してください)。
さて、95%信頼区間の正確な意味ですが、「母集団からサンプルを取り出して、信頼区間を求めることを何度も繰り返すと、母数がそれらの信頼区間の中に入っている確率が95%である」ということです。
母数は、得られた多数の信頼区間の中に入っているか、入っていないかのどちらかです。その「入っていた」回数が全体の95%になるというわけです(図3)。念のためにまとめると、「母数が95%の確率で信頼区間に含まれる」と考えるのではなく「得られた多数の信頼区間のうちの95%に母数が含まれる」と考えるべきです。
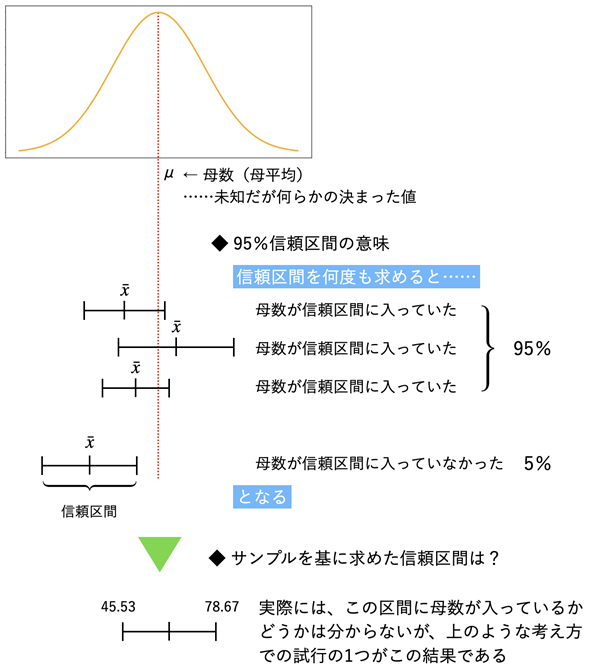 図3 区間推定における95%信頼区間の意味
図3 区間推定における95%信頼区間の意味信頼区間を求めたとき、母数はその信頼区間に入っているか、入っていないかのいずれかである。95%信頼区間の意味は、信頼区間を何回も求めたとき、そのうちの95%の回に母数が信頼区間に入っている、という意味。得られたサンプルから計算して求めた信頼区間は、そのような試行の1つと考えられる。
図2に示した例は、このような考え方の下で、得られたサンプルから計算して求めた母平均の95%信頼区間が45.53<μ<78.67、母分散の95%信頼区間が253.85<σ2<1788.22であった、ということです(別のサンプルを基に95%信頼区間を求めると、これとは違った値になるかもしれません)。
未知の母数が、サンプルから得られた信頼区間に入っているかどうかは(確定はしているのですが)実際には分かりません。気持ち的には、上のような考え方で求められた信頼区間なので、95%の信頼度が持てると考えることはできます。しかし、厳密には、「95%の確率で母数がこの信頼区間に含まれる」と言うわけにはいきません。何とも回りくどい考え方のように思われるかもしれませんが、図3の「信頼区間の意味」の部分で示した考え方が信頼区間の正確な意味だというわけです。
なお、ここで見た95%という値は信頼水準または信頼係数と呼ばれる値で、一般に、
と表されます。αは有意水準と呼ばれる値で、5%(=0.05)などの値がよく使われます。α=0.05のとき、信頼水準は100×(1−0.05)%=95%となります。
区間推定は、この連載の続きに予定している仮説検定の基礎として位置付けることができます。区間推定では「母数の推定」を行い、仮説検定では「仮説が支持されるかどうかを判断する」というように目的は異なりますが、ほぼ同じ計算方法を使います。考え方には持って回ったようなわずらわしさを感じるかもしれませんが、計算の方法は比較的簡単です。ご心配なく!
さまざまな区間推定 〜 この連載で取り扱う内容
というわけで、この連載では、さまざまな確率分布に従う母集団の母数について、Excelを使って手を動かしながら、区間推定を行う方法を学んでいきます。予定としては、表1のように進めていくつもりですが、話の流れによっては内容や事例などを変更することがあるかもしれません。
| 回 | テーマ | 主な内容 |
|---|---|---|
| 1 (今回) | 推測統計(区間推定編)の連載開始! | 推測統計とは、点推定と区間推定の考え方、信頼区間の意味 |
| 2 | 母平均の区間推定 | 資格試験の平均点を区間推定しよう |
| 3 | 母分散の区間推定 | スマホ利用時間の分散はどれぐらい? |
| 4(番外編) | ベイズ統計の確信区間とは | 頻度主義の信頼区間とベイズ主義の確信区間の違いって何? |
| 5 | 母平均の差の区間推定 | 公立/私立の学力テストの差はどれぐらい? |
| 6 | 母分散の比の区間推定 | 新しい機械で製品のばらつきはどれぐらい小さくなった? |
| 7 | 相関係数の区間推定 | BMIの値と糖尿病の進行の相関にはどの程度の幅がある? |
| 8(番外編) | サンプルサイズの決め方 | 誤差を一定の範囲に抑えるには何件のデータが必要? |
おおむね、この表の流れにそって、さまざまな区間推定の方法について説明していく。流れによって内容や事例が変わるかもしれないが、取りあえずは、だいたいの雰囲気を捉えるだけで十分。
すでに触れたように、正規分布の場合、点推定の計算はこれまでにやってきた平均や不偏分散の計算だけです。これらについては、あらためて見るまでもないかもしれませんが、一応、以下のコラムで解説しておきます(ただし、後半で、あまり知られていない話も少しします)。区間推定による信頼区間の求め方については、次回以降のお楽しみということにしましょう。
コラム 点推定による母平均と母分散の推定例
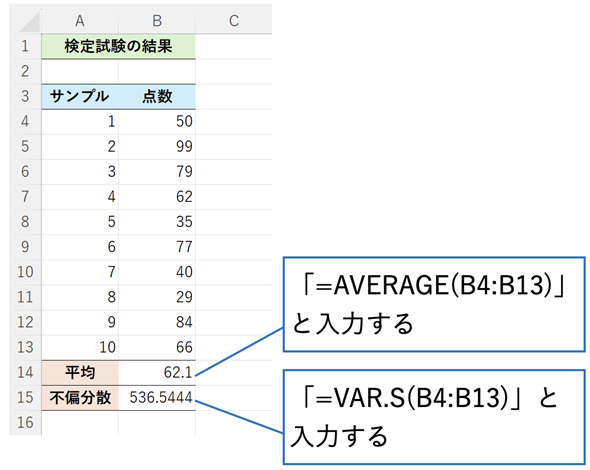
本文で触れたように、点推定ではデータの算術平均が母平均の推定値となり、不偏分散が母分散の推定値となります。おさらいがてら、AVERAGE関数とVAR.S関数を使って計算してみましょう。
サンプルファイルをこちらからダウンロードし、[点推定]ワークシートを開いて試してみてください。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから[ファイル]−[コピーを作成]を選択し、Googleドライブにコピーしてお使いください。操作方法は図4に記した通りです。
さて、ここから知る人ぞ知るお話をします。母標準偏差の推定値としては、不偏標準偏差が使われます。不偏標準偏差の値は、一般に不偏分散のルート(正の平方根)で求められます。ExcelではVAR.S関数のルートを求めてもいいですが、STDEV.S関数を使えば不偏標準偏差の値が簡単に求められます。
しかし、不偏標準偏差の厳密な値は、以下のようにガンマ関数を使って補正した式で求められます(理由はかなり難しいので割愛します)。Γがガンマ関数です。枠で囲んだ部分は標本標準偏差です。
Excelで計算してみましょう。ガンマ関数の値はGAMMA関数で、標本標準偏差の値はSTDEV.P関数で求められます。サンプルファイルの[補正された不偏標準偏差]ワークシートを開いて試してみてください。操作方法は図5に記した通りです。
 図5 補正された不偏標準偏差を計算する
図5 補正された不偏標準偏差を計算するセルB15のSTDEV.S関数で求めた値は不偏分散のルートの値。セルB18が(1)式に基づいて計算した値。小数点以下に違いがあるが、実用的にはセルB15の値を使う。
実際のところ、サンプルサイズが大きくなると差が小さくなることもあり、実用的には不偏分散のルートが不偏標準偏差の値として使われます。
繰り返しになりますが、区間推定は仮説検定の基礎としても位置付けられます。これから、一歩ずつ着実に進めていけるように、やさしく説明するつもりです。次回からの連載にぜひご期待ください。
この記事で取り上げた関数の形式
関数の利用例については、この記事の中で紹介している通りです。ここでは、連載で初出となる関数の基本的な機能と引数の指定方法だけを示しておきます。
補正された不偏標準偏差を計算するために使った関数
GAMMA関数:ガンマ関数の値を求める
形式
GAMMA(x)
引数
- x: ガンマ関数の値を求めるための数値を指定する。
Copyright© Digital Advantage Corp. All Rights Reserved.


 羽山博
羽山博