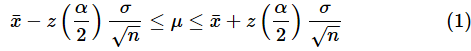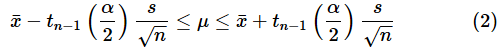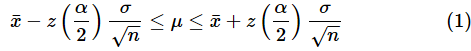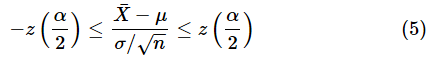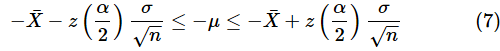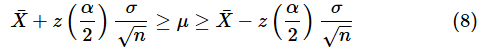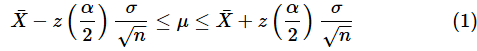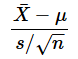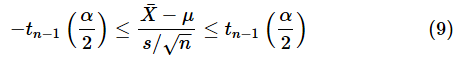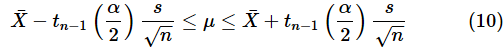［データ分析］母平均の区間推定 〜 テストの平均点、どこまで信頼できる？：やさしい推測統計（区間推定編）

データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載（区間推定編）の第2回。区間推定の第一歩として、正規分布する母集団の平均（＝母平均）を区間推定する方法と考え方を解説します。

[羽山博，著]

連載目次

連載：

『社会人1年生から学ぶ、やさしい推測統計（区間推定編）』

　この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』シリーズの「記述統計と回帰分析編」「確率分布編」に続く「推測統計（区間推定編）」です。
　この連載では、観測されたデータを基に、母集団の母数について区間推定を行う方法を説明します。身近に使える表計算ソフト（Microsoft ExcelやGoogleスプレッドシート）を使いながら具体的に事例を見ていきます。
　必要に応じて、Pythonのプログラムなどでの作成例にも触れることにしますが、数学などの前提知識は特に問いません。肩の力を抜いてぜひとも気楽に読み進めてください。

羽山博

筆者紹介： IT系ライターの傍ら、非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。健康のために始めたウォーキングの友として、歩数によって経験値やアイテムが獲得できるゲームを始めるも、自宅でできるバトルに夢中になりすぎてむしろインドア化に拍車がかかった感も。最近、欲しいと思っているものは柔軟な身体と鋼のメンタル。大切だと思っていることは車間距離。

　データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の推測統計（区間推定編）、第2回です。前回は出発点として、区間推定の考え方について解説しました。今回は正規分布する母集団（正規母集団）の母平均を区間推定する具体的な方法とその考え方を見ていきます。

母平均を区間推定するための基本的な考え方

　区間推定とは、一定の幅を持たせて母平均や母分散などの母数を推定することです。基本的な考え方については前回お話しした通りです。その「幅」のことを信頼区間と呼ぶということでした。

　今回からは具体的な例を使って、区間推定を行っていきます。今回取り上げるのは、母平均の区間推定です。最初に、母平均を区間推定するための大まかな考え方と手順を図解しておきます。図1は、ある会社の社員が受験した資格試験（テスト）の例です。母集団となるのは社員全体です（（1））。しかし、社員全員が受験するのは難しいので、ランダムに抽出された何人かの社員が受験したものとしています。その結果（成績）がサンプル（標本）の値となります（（2））。このサンプルを基に、母平均を区間推定するという流れです（（3））。

　前回、信頼区間の意味として「例えば、95％信頼区間とは、信頼区間を何回も求めたとき、その試行の95％に当たる回に母数が含まれている」ということだとお話ししました。そのような考え方の下でサンプルから母平均の95％信頼区間を求めたところ、図1のような結果が得られたというわけです。

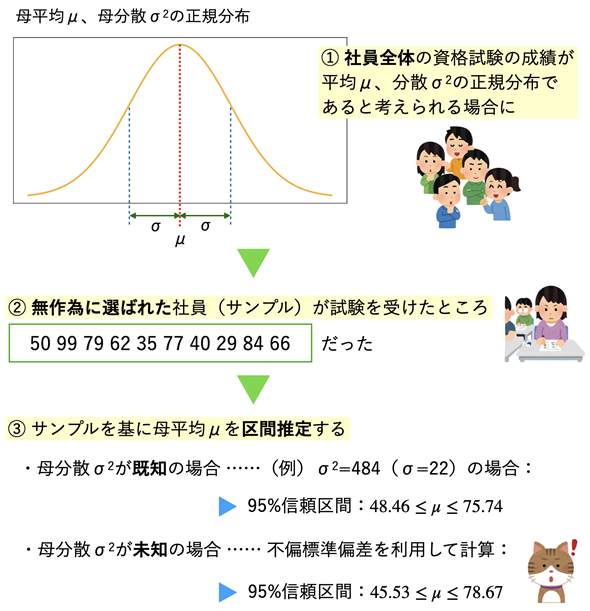図1　母平均を区間推定するための考え方と手順
母集団が正規分布するという前提の下、母集団から取り出されたサンプルを基に母平均を区間推定する。母分散σ²が既知の場合と未知の場合では計算方法が異なることに注意（計算方法は後述）。

　図1では、母集団が正規分布に従うことを前提としていますが、実は、サンプルサイズがおおむね30以上で、極端な外れ値や分布の偏りがなければ、母集団の分布はどのようなものでも構いません（その理由は後述します）。

　ここで重要となるのは、図中にも示したように、母分散σ²が既知の場合と未知の場合では計算方法が異なることです。もちろん、結果も異なってきます。

　取りあえず、信頼区間を求めるためのそれぞれの式を以下に示しておきます。かなり複雑な式に、ちょっとたじろいでしまいそう……という方は、見なかったことにして先に進んでもらっても全く問題ありません。実際にExcelの関数を使って計算すると、とても簡単だということが分かります。ご心配なく。

母分散が既知の場合の信頼区間

*　標準正規分布については、確率分布編の記事を参考にしてください。

　実際のところ、母分散σ²が既知である場合というのはあまり考えにくいのですが、サンプルサイズが大きい場合（おおむね100件以上の場合）は、母分散が未知であっても、「母標準偏差σの値」の代わりに「標本標準偏差の値」を用いて、上記の式を近似的に適用することもできます。

母分散が未知の場合の信頼区間

*　t分布については、確率分布編の記事を参考にしてください。

　では、Excelを使ってサクッと信頼区間を求めてみましょう。

母平均を区間推定してみよう（母分散が既知の場合）

　Excelには、母分散が既知の場合に母平均の区間推定を行うための関数としてCONFIDENCE.NORM関数が用意されています。サンプルファイルをこちらからダウンロードし、［母平均の区間推定 (母分散が既知)］ワークシートを開いて試してみてください。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから［ファイル］−［コピーを作成］を選択し、Googleドライブにコピーしてお使いください。操作方法は図2に記した通りです。

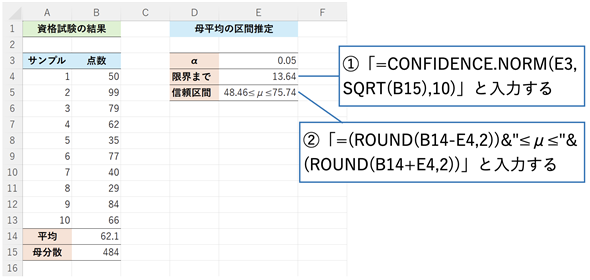図2　CONFIDENCE.NORM関数を使って信頼区間を求める
CONFIDENCE.NORM関数で求めたセルE4の値をサンプルの平均から引いた値が信頼区間の下限、平均に足した値が信頼区間の上限となる。セルE5では信頼区間を見やすくするため、ROUND関数を使って小数点以下2桁まで求めた値と「≤μ≤」という文字列を連結している（&演算子は文字列を連結する演算子）。なお、セルB15の母分散はVAR.P関数やVAR.S関数で求めたものではなく、既知の分散である484を入力したもの。CONFIDENCE関数にはそのルートを指定してある。

　CONFIDENCE.NORM関数には、引数として有意水準αの値、母標準偏差、サンプルサイズを指定します。結果は13.64となりました。この値をサンプルの平均から引いた48.46が信頼区間の下限となり、サンプルの平均に足した75.74が信頼区間の上限となります。

　最初の引数に指定する有意水準αの値としては、0.05（＝5％）や0.01（＝1％）が使われるのが一般的です。α＝0.05の場合、(1−α)×100％ ＝ 95％なので、95％信頼区間が求められます。α＝0.01の場合は(1−α)×100％ ＝ 99％なので、99％信頼区間となります。αの値が小さくなるほど信頼区間の幅が広くなります。試しに、サンプルファイルのセルE3の値を0.01としてみてください。セルE4の値が17.92となり、セルE5に表示される信頼区間は44.18≤μ≤80.02となります。

　ここでは、1回のサンプルから95％信頼区間や99％信頼区間を求めています。ただし、この1回の信頼区間に、本当のテストの平均点（＝社員全員の母平均）が含まれているかどうかは分かりません。しかし、同じ方法で何度も信頼区間を計算すると、長期的に見て95％／99％の信頼区間には母平均が含まれることが保証されます。これが、今回の記事のサブタイトル「テストの平均点、どこまで信頼できる？」への答えとなります。

　なお、CONFIDENCE.NORM関数は本来、母分散が既知の場合に使いますが、上でも述べたように、サンプルサイズが大きい場合は母分散が未知の場合でもCONFIDENCE.NORM関数に（母標準偏差σの推定値として）標本標準偏差を代わりに指定して信頼区間を近似的に求めることができます。その場合は、CONFIDENCE.NORM関数の2番目の引数にVAR.P関数で求めた標本分散のルートを指定するか、STDEV.P関数で求めた標本標準偏差を指定します。

　続いて、母分散が未知の場合の例です。一般的には、母分散が未知の場合に先ほどのような標準正規分布を使った数式（CONFIDENCE.NORM関数）を使うのではなく、以下の方法を用います。

母平均を区間推定してみよう（母分散が未知の場合）

　母分散が未知の場合は、CONFIDENCE.T関数を使います。引数として指定する値は、有意水準αの値、不偏標準偏差、サンプルサイズです。サンプルファイルの［母平均の区間推定 (母分散が未知)］ワークシートを開いて試してみてください。操作方法は図3に示した通りです。

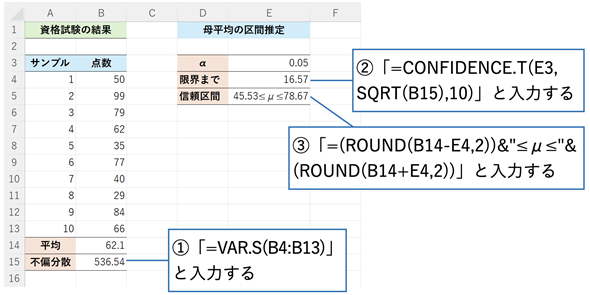図3　CONFIDENCE.T関数を使って信頼区間を求める
CONFIDENCE.T関数の2つ目の引数には不偏標準偏差を指定する。この例ではセルB15でVAR.S関数を使って不偏分散を求めているので、そのルートを指定している。セルE5の式は図2と同じ。

　CONFIDENCE.T関数には、引数として有意水準αの値、不偏標準偏差、サンプルサイズを指定します。得られた信頼区間は45.53 ≤μ ≤ 78.67となりました。

　いかがでしょう。結局のところ、CONFIDENCE.NORM関数やCONFIDENCE.T関数を入力するだけなので、答えは簡単に求められましたね。

　ここまでに条件が幾つか出てきたので、混乱しているかもしれません。あらためて表にまとめておくので、頭の中を整理するのにご活用ください。

母分散	利用する分布	利用する標準偏差（Excel関数での計算方法）
既知の場合（母分散σ2の値が分かっている場合）	標準正規分布（＝z分布）	既知の母標準偏差σの値を使う
未知の場合（サンプルサイズが大きく、近似的でもよい場合）	標準正規分布を近似的に使う	母標準偏差の推定値を使う（VAR.P関数で全データの分散を求め、そのルートを取る、またはSTDEV.P関数を使う）
未知の場合（通常のケース）	t分布（自由度：n−1）	不偏標準偏差sを使う（VAR.S関数で不偏分散を求め、そのルートを取る、またはSTDEV.S関数を使う）
表1　母分散の条件に応じた適用分布と標準偏差の計算方法

信頼区間はどのように計算されるか

　さて、いよいよ信頼区間を計算する（1）式と（2）式がどのようにして導き出されたかをお話しします。単に答えを求めるだけでなく、やはり意味も深く理解しておきたいですね。まず、母分散が既知の場合から見ていきます。

母平均の信頼区間を導き出そう（母分散が既知の場合）

　母分散が既知の場合、母平均の信頼区間は（1）式で表されました。再掲しておきます。

　この式を導き出す前に、

で表される、標準正規分布のα/2点とは何かを確認しておきましょう（図6）。

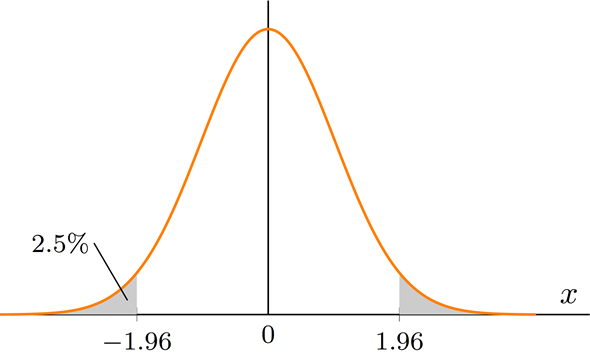図4　標準正規分布の2.5％点
グラフは標準正規分布の確率密度関数。アミカケの部分が累積確率となる。α＝5％であれば、α/2＝2.5％。このときのα/2％点は、左側（下側）のアミカケ部分が全体の面積の2.5％となるようなxの値のこと。右側（上側）のアミカケ部分と合わせれば5％となる。

　標準正規分布は平均が0、分散が1の正規分布です。α/2％点とは、累積分布関数の値がα/2％となるxの値のことです。そして、標準正規分布のα/2％点は、

と表されます。

　図4の例であれば、α＝5％、つまり、α/2＝2.5％ですね。従って、この場合の

の値は、左側（下側）の累積確率（アミカケの部分の面積）が全体の面積の2.5％となるxの値です。後で実際に計算してみますが、結果は

となります。標準正規分布は平均値の0を中心とした左右対称の分布なので、右側（上側）のx＝1.96以上の累積確率も2.5％です。両方合わせると5％になります。

　では、次に進みます。ちょっと話は変わりますが、平均μ、分散σ²の母集団からn個のサンプル（X₁,X₂,…,X_n）を取り出し、

を求めることを繰り返したとしましょう（大文字のXを使っているのは、個々の具体的な値ではなく確率変数であることを一般的に表すためです）。このとき、母集団がどのような分布であっても、

は平均μ、分散σ²/nの正規分布に近づきます。「え、何それ？」と思った方もおられるかもしれまんが、これは確率分布編でお話しした中心極限定理にほかなりません。

　正規分布をNと表すと、このことは、

と書けます。∼は「確率変数がある分布に従う」という意味でした。

　この分布は、個々のサンプルの値であるX_iの分布ではなく、

であることに注意してください。

　次に（3）式を標準化して、平均が0に、分散が1になるように調整しましょう。

から平均μを引いて、標準偏差σ/√nで割ればいいですね。すると、（4）式の左辺のようになります。右辺は標準正規分布を表します。

　標準正規分布のα/2点を

とすると、（4）式が

から

の範囲に入ることは、以下のように表せます。

　これをμについて解きます。両辺にσ/√nを掛けましょう。

　両辺に−1を掛けます。不等号の向きが逆になります。

　（8）式を小さい順に並べましょう。

ということで、ちゃんと（1）式と同じ形になりました。最初の方の注釈で触れたように、サンプルサイズが大きければ（おおむね30以上であれば）、母集団がどのような分布であっても、母平均の区間推定ができます。それは、中心極限定理が根拠となっている、ということですね。

母平均の信頼区間を導き出そう（母分散が未知の場合）

　母分散が未知の場合、母平均の信頼区間は（2）式で表されました。こちらも再掲しておきます。

　こちらもグラフで確認しておきます（図5）。

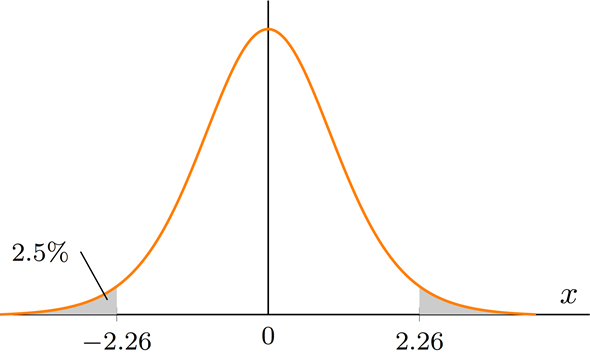図5　自由度9のt分布の2.5％点
グラフは自由度9のt分布の確率密度関数。アミカケの部分が累積確率となる。α＝5％であれば、α/2＝2.5％。このときのα/2％点は、左側（下側）のアミカケ部分が全体の面積の2.5％となるようなxの値のこと。右側（上側）のアミカケ部分と合わせれば5％となる。

　t分布でも考え方は同じです。t分布のα/2％点とは、t分布の累積分布関数の値がα/2％となるxの値のことです。図5を見れば、

の値が-2.26であることが分かります。t分布も平均の0を中心とした左右対称の分布なので、右側（上側）のx＝2.26以上の累積確率も2.5％です。両方合わせると5％になります。

　では、信頼区間の式を見ていきます。母分散が未知の場合は、母標準偏差σの代わりに不偏標準偏差sを使います。その場合、

の分布は自由度n−1のt分布に従います。母分散が既知の場合の例と同じように、t分布の−α/2点からα/2点の範囲は

となります。以降の計算も同様に進められるので、結果だけを示しておきます。この不等式をμについて解けば、

が得られます。

　信頼区間を求めるための式が導き出せたので、以上で、めでたく母平均の区間推定のお話は終わり……といきたいところですが、せっかく（1）式や（2）式で信頼区間の定義を示したので、CONFIDENCE.NORM関数やCONFIDENCE.T関数を使わず、

の値を求め、上で見た式に従って信頼区間を求めてみたいですね（そんなことはないですか？）。以下のコラムにまとめておきます。

コラム　信頼区間を定義通りに計算する

　累積確率分布におけるα/2点とは、累積確率がα/2になる点の値（確率変数の値）です。従って、累積分布関数に対する逆関数の値を求める必要があります。

　標準正規分布の場合、累積分布関数の逆関数の値はNORM.S.INV関数で求められます。また、t分布の場合、累積分布関数の逆関数の値はT.INV関数で求められます。

　というわけで、計算の手順を図6、図7にまとめて掲載することにします。サンプルファイルの［定義通りに (母分散が既知)］ワークシートと［定義通りに (母分散が未知)］ワークシートを開いて試してみてください。

　母分散が既知の場合の信頼区間は以下のようにして求められます（図6）。

図6　定義通りに信頼区間を求める（母分散が既知の場合）
標準正規分布のα/2点を求めるには、NORM.S.INV関数にα/2の値を指定すればよい。ただし、左側（下側）からの累積確率がα/2となる点なので、答えは負になる。そのためABS関数を使って絶対値を求めてある。セルE5の式でα/2点の値にσ/√nを掛けた値を求めている。ここでは、セルB5の値が母標準偏差ではなく母分散であることに注意。従って、セルE5の式に含まれる「SQRT(B5/B3)」は、√(σ²/n)＝σ/√nを表す。

　セルE4で求めたα/2点の値が1.96となっていることに注目してください。図4に示した-1.96や1.96という値はこのようにして求めたものです。

　続いて、母分散が未知の場合の信頼区間です（図7）。

図7　定義通りに信頼区間を求める（母分散が未知の場合）
自由度n-1のt分布でα/2点を求めるには、T.INV関数にα/2の値と自由度を指定する。t分布の場合も、α/2点は左側（下側）からの累積確率がα/2となる点なので、答えは負になる。そのためABS関数を使って絶対値を求めてある。セルE5の式でα/2点の値にs/√nを掛けた値を求めている。ここでは、セルB5の値が不偏標準偏差ではなく不偏分散であることに注意。従って、セルE5の式に含まれる「SQRT(B5/B3)」は、√(s²/n)＝s/√nを表す。

　こちらでは、セルE4で求めたα/2点の値が2.26となっています。図5に示した値はこのようにして求めたというわけです。なお、T.INV.2T関数では両側確率に対する逆関数の値（xに当たる値のうち正の値）が求められるので、図5の例でセルE4に「=T.INV.2T(E3,B3-1)」と入力しても同じ結果が得られます。

---

　今回は、母平均の区間推定について、Excelの関数を使って計算の手順から始め、信頼区間を表す式の意味を解説しました。

　次回は、母分散の区間推定を見ていきます。取り扱う母数は異なりますが、基本的な手順や考え方は今回と同じです。続けて読み進めていただくと、信頼区間の計算方法や式の意味に対する理解がさらに深まると思います。次回をお楽しみに！

この記事で取り上げた関数の形式

　関数の利用例については、この記事の中で紹介している通りです。ここでは、連載で初出となる関数の基本的な機能と引数の指定方法だけを示しておきます。

信頼区間を求めるために使った関数

CONFIDENCE.NORM関数： 正規分布を利用して母平均の信頼区間を求める

形式

CONFIDENCE.NORM(α, 標準偏差, サンプルサイズ)

引数

• α： 有意水準を指定する。(1−α)×100％信頼区間が求められる。
• 標準偏差： 母集団の既知の標準偏差を指定する。
• サンプルサイズ： 母集団から取り出したデータの個数を指定する。

備考

※CONFIDENCE.NORM関数で求められる値は、平均から信頼区間の下限または上限までの幅です（信頼区間全体の幅の半分に当たります）。

CONFIDENCE.T関数： t分布を利用して母平均の信頼区間を求める

形式

CONFIDENCE.T(α, 不偏標準偏差, サンプルサイズ)

引数

• α： 有意水準を指定する。(1−α)×100％信頼区間が求められる。
• 不偏標準偏差： 母集団の標準偏差の推定値を指定する。
• サンプルサイズ： 母集団から取り出したデータの個数を指定する。

備考

※CONFIDENCE.T関数で求められる値は、平均から信頼区間の下限または上限までの幅です（信頼区間全体の幅の半分に当たります）。

「やさしい推測統計（区間推定編）」

AI・データサイエンスの学びをここから

初心者向け、データ分析・AI・機械学習・Pythonの勉強方法　＠ITのDeep Insiderで学ぼう