　前回は、scikit-learnが提供するDiabetesデータセットを例として、単回帰分析をしてみました。具体的には、BMI値から1年後の糖尿病の進行具合（ターゲット）を予測しました。その結果は決定係数「R²」が0.42とそれほど高くはないが最悪でもない（ある程度、予測がターゲットに当てはまっている）というものでした。

　そこで、今回はBMI値に加えて幾つかの特徴量を使った重回帰分析を行い、モデルの精度が上がるかどうかを見ていくことにしましょう。ここでは前々回に保存したCSVファイルを使用します。これは以下に示す列で構成され、Zスコア標準化などを行ったものです（かっこ内の数値はtarget列との相関係数）。

bmi：BMI（0.59）
bp：血圧（0.44）
s3：善玉コレステロール（-0.39）
s4：総コレステロール値／善玉コレステロール（0.43）
s5：中性脂肪（0.57）
s6：血糖値（0.38）

　まずは以下のコードでpandasやNumpy、Matplotlibや必要な関数やクラスをインポートし、前々回に保存したデータセットを読み込みます。

import pandas as pd
import numpy as np

df_org = pd.read_csv('diabetes.csv')
df_org

pandasとNumPyとscikit-learnのインポート、CSVファイルの読み込み

　今回は（試行錯誤の末に）target列を平均0、分散1となるように標準化しておくことにしました。

mu_y = df_org['target'].mean()
sigma_y = df_org['target'].std()
df_org['target_std'] = (df_org['target'] - mu_y) / sigma_y
df_org['restored_target'] = df_org['target_std'] * sigma_y + mu_y
print(np.allclose(df_org['restored_target'], df_org['target']))
df_org = df_org.drop('restored_target', axis=1)

平均0、分散1となるようにtarget列を標準化

　target列を標準化することで、後で出てくる回帰係数をより素直に解釈できるようになります。また、テストデータをモデルに与えて予測した結果は標準化後の列（target_std列）と比較して誤差を計算できますが、実際に1年後の進行具合の値を得るには、標準化前の値に戻す必要があります（予測値×標準偏差＋平均値で求められます）。上のコードでは、標準化したtarget_std列の値に標準偏差を掛け、平均値を加算した結果をrestored_target列に保存し、NumPyのallclose関数で変換後の値と変換前の値が等しいかどうかを確認しています（確認後、restored_target列は削除しています）。進行具合の値が必要になったときには「予測値×標準偏差＋平均値」という変換をする必要があるでしょう（今回はそこまでやる予定はありません）。

　Visual Studio Codeで実行した結果を以下に示します。Trueと表示されているので、逆方向へ正しく変換できていることが分かります。

実行結果

　読み込んでtarget列を標準化したデータセットはdf_orgに保存しておき、この後はdf_orgから必要な列を選択し、訓練データとテストデータに分割してから、重回帰分析していくことにします。データ分割用の関数と作成したモデルを使って予測を行う関数は前回の最後で定義したものを使います（ただし、標準化後のtarget_std列を使うように変更しています）。

from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score

def split_data(df, rows=None, rs=765):
    if rows is None:
        rows = ['bmi']
    X = df[rows]
    y = df[['target']]
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=rs)
    return X_train, X_test, y_train, y_test

def fit_and_predict(model, X_train, y_train, X_test, y_test):
    model.fit(X_train, y_train)
    y_pred = model.predict(X_test)

    r2 = r2_score(y_test, y_pred)
    return r2, y_pred

前回作成した関数

単回帰分析をもう一度

　まずは、これらの関数を使って、単回帰分析すると次のようになります。これは前回のおさらいという意味もありますが、重回帰分析でR²の値がどう変わるのか、そのスタート地点の確認です。

from sklearn.linear_model import LinearRegression

cols = ['bmi']
X_train, X_test, y_train, y_test = split_data(df_org, ['bmi'])
model = LinearRegression()
r2, y_pred = fit_and_predict(model, X_train, y_train, X_test, y_test)
print(r2)

単回帰分析するコード

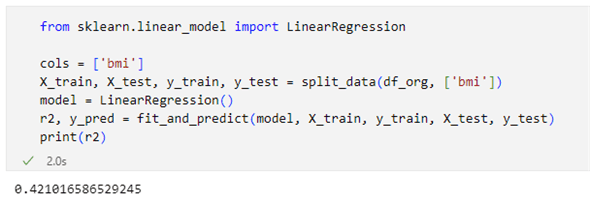
　実行結果を以下に示します。

実行結果

　前回同様、R²が0.42程度になっていることが確認できました。これが重回帰分析でどのくらい良くなるのか、今から試していきましょう。

BMIと血圧を特徴量とする

　ではBMIと血圧の2つを特徴量として選択し、モデルの作成と予測を行ってみます。

cols = ['bmi', 'bp']
X_train, X_test, y_train, y_test = split_data(df_org, cols)
model = LinearRegression()
r2, y_pred = fit_and_predict(model, X_train, y_train, X_test, y_test)
print(r2)

BMIと血圧の2つから訓練と推測を行うコード

　実行結果を以下に示します。

実行結果。R²が向上した

　単回帰分析のときのR²の値は「0.42」くらいでしたが、今回は「0.48」くらいまで改善されたことが分かります。特徴量が1つ増えるだけでも（相関が強かったとはいえ）、それなりに変わるものですね。

　続けて、特徴量を増やしてどうなるかを確認してもよいのですが、その前に回帰係数も確認しておきましょう。ここではBMIと血圧の2つを特徴量としてモデルを訓練しました。つまり、「y＝w₀×x₀＋w₁＋x₁＋b」のような式で、BMIと血圧と1年後の糖尿病の進行具合をモデル化したといえます。回帰係数はこのw_nの値のことです。bは切片です（全ての特徴量が0の場合の予測値ともいえます）。x_nに2つの特徴量の値が代入されます。

　大ざっぱな言い方をすれば、回帰係数のw₀やw₁はBMIや血圧が1増加すると、1年後の進行具合がどの程度変化するかを示す値です。回帰係数はモデルのcoef_属性にまとめられています。また、切片はintercept_属性で取得できます。そこで、次のコードでそれらを取り出してみましょう。

coefficients = {col: val for col, val in zip(cols, model.coef_.squeeze())}
print('coefficients:', coefficients)
intercept = model.intercept_
print('intercept:', intercept)

回帰系素と切片がどうなっているかを表示

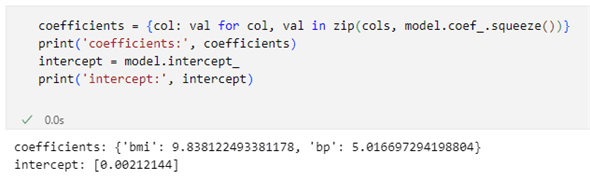
　実行結果は次の通りです。

実行結果

　BMIの回帰係数は9.838、血圧の回帰係数は5.016、切片は0.002となりました（切片が0に近い値になっているのは、target列を標準化したからです）。このことからはBMIの方が血圧よりも1年後の進行具合に対する影響が強い可能性が高いといえます（断言はできません）。

　回帰係数に加えて、MAE（Mean Average Error：平均絶対誤差）とRMSE（Root Mean Squared Error：平均二乗誤差の平方根）についても見てみましょう。前者は予測値と正解値の差（絶対値）の平均を求めたもので、後者は予測値と正解値の差を二乗したものの平均を求めたものです。どちらも予測がどのくらい正解に近いかを示す指標となります。

　MAEはscikit-learnのmean_absolute_error関数で、平均二乗誤差はmean_squared_error関数で計算できます（よって、平均二乗誤差の平方根はmean_squared_error関数の結果の平方根を取ります）。

from sklearn.metrics import mean_absolute_error, mean_squared_error

mae = mean_absolute_error(y_test, y_pred)
print('mae:', mae)
rmse = np.sqrt(mean_squared_error(y_test, y_pred))
print('rmse:', rmse)

MAEとRMSEを計算

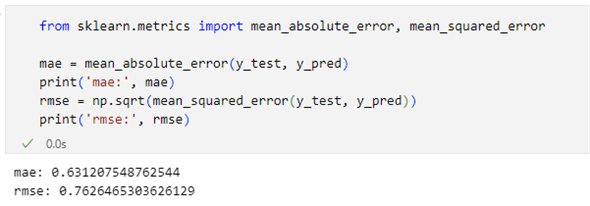
　実行結果を以下に示します。

実行結果

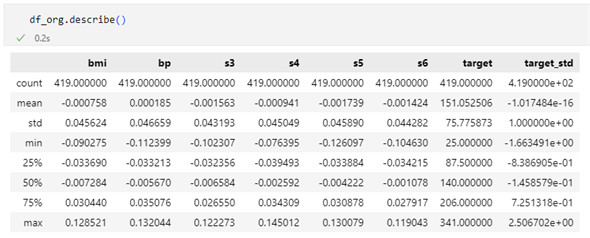
　MAEは0.631、RMSEは0.763くらいになっています。ここで「df_org.describe()」を実行して、target_std列の最小値と最大値を確認してみましょう。

右端にあるtarget_std列の最小値は-1.663、最大値は2.507

　target_std列は-1.663～2.507の範囲（2.507-(-1.663)= 4.17）にあります。これとMAEの0.631、RMSEの0.763を見比べてみると、その比率は0.631/4.17=0.151、0.763/4.17=0.183くらいといえます。この比率は、標準化後のターゲットのばらつき（最小～最大）に対して、予測値と正解値の誤差がどの程度の大きさかをざっくりと示すもので、おおよそ15％とか18％となっています。これを0％に近づけられればモデルの性能はもっと良くなっていくでしょう。

　そのためには、特徴量を追加していきながら、これらの値がどう変化していくかも見ていきます。

BMI／血圧／善玉コレステロールを特徴量とする

　次に負の強い相関関係がある善玉コレステロール（s3列）を含めて重回帰分析してみます。コードはこれまでと同様です。

cols = ['bmi', 'bp', 's3']
X_train, X_test, y_train, y_test = split_data(df_org, cols)
model = LinearRegression()
r2, y_pred = fit_and_predict(model, X_train, y_train, X_test, y_test)
print(r2)

BMI、血圧、善玉コレステロール値を使った重回帰分析

　実行結果は以下の通りです。

実行結果。さらにR²が向上した

　R²は「0.498」とさらに良くなりました。

　回帰係数とMAE、RMSEはどうでしょう。

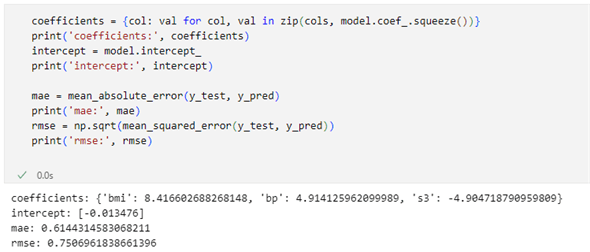
coefficients = {col: val for col, val in zip(cols, model.coef_.squeeze())}
print('coefficients:', coefficients)
intercept = model.intercept_
print('intercept:', intercept)

mae = mean_absolute_error(y_test, y_pred)
print('mae:', mae)
rmse = np.sqrt(mean_squared_error(y_test, y_pred))
print('rmse:', rmse)

回帰係数とMAE、RMSE

　実行結果を以下に示します。

実行結果。MAEは0.631から0.614に、RMSEは0.763から0.751にわずかだが減少した

　回帰係数はBMI：8.417、血圧：4.914、善玉コレステロール：-4.905となりました。MAEは0.631から0.614に、RMSEは0.763から0.751にわずかですが減少しました。モデルの性能を高めるには、善玉コレステロールも特徴量と選択してもよさそうです。

その他の特徴量をまとめて

　さらに1つずつ特徴量を追加していきながら、同じようなコードを繰り返そうと思ったのですが、面倒くさいのでそれはやめにして、以下では今見た3つに加えて、s4列、s5列、s6列を順番に特徴量として追加し、訓練とテストを行って、R²、回帰係数、MAE、RMSEを確認するコードを書きました。

cols0 = ['bmi', 'bp', 's3', 's4']
cols1 = ['bmi', 'bp', 's3', 's4', 's5']
cols2 = ['bmi', 'bp', 's3', 's4', 's5', 's6']
cols_list = [cols0, cols1, cols2]

results = []
for cols in cols_list:
    X_train, X_test, y_train, y_test = split_data(df_org, cols)
    model = LinearRegression()
    r2, y_pred = fit_and_predict(model, X_train, y_train, X_test, y_test)
    coefficients = {col: val for col, val in zip(cols, model.coef_.squeeze())}
    intercept = model.intercept_
    mae = mean_absolute_error(y_test, y_pred)
    rmse = np.sqrt(mean_squared_error(y_test, y_pred))
    results.append([r2, coefficients, intercept, mae, rmse])

for cols, item in zip(cols_list, results):
    print(f'cols: {cols}')
    print(f' r2: {item[0]:.4f}')
    for name, val in item[1].items():
        print(f' {name}: {val:.4f}', end='')
    print()
    print(f' intercept: {item[2][0]:.4f}')
    print(f' mae: {item[3]:.4f}', end='')
    print(f' rmse: {item[4]:.4f}')

BMI、血圧、善玉コレステロールに加えてコレステロール比、中性脂肪、血糖値を特徴量として選択して訓練とテストを行う

　結果は次の通りです。

実行結果

　s4列（善玉コレステロール）とs5列（中性脂肪）を順に追加することで、モデルの性能が上がっているようです（R²、MAE、RMSEに注目）。しかし、一番下のs6列（血糖値）を特徴量として追加した場合の結果を見ると、その上の結果よりもわずかですがR²やMAE、RMSEが低下していることが分かります。s6列は特徴量として選択する必要はなさそうです。

　以上のことから、このモデルではBMI、血圧、善玉コレステロール、コレステロール比、中性脂肪を特徴量として選択するのがよいでしょう。また、単回帰分析と比べて、R²は0.42から0.538に向上しました。

　MAEとRMSEについても、BMIと血圧のみを特徴量としたときと比べて、MAI：0.63→0.57、RMSE：0.76→0.72と着実に減少しています。

　実際には多重共変性の有無をチェックしたり、残差分析（＝「正解値－予測値」で計算される残差を図で可視化し、モデルのズレ方を観察して確認する分析方法）をしたり、別の方法を考えたりと、他にもやれることはあります。しかし、本連載ではここまでとすることにします。最後はpandasというよりも、scikit-learnについてお話になっていましたが、pandasだけで全てができるというわけではなく、優れたフレームワークをうまく組み合わせて、自分がやりたいことを実現できるようにいろいろな技術に慣れていくようにしましょう。

「Pythonデータ処理入門」

この連載を「連載記事アラート」に登録する New