[pandas超入門]Diabetesデータセットを使って回帰分析してみよう(前処理編):Pythonデータ処理入門
箱ひげ図や四分位範囲を用いた外れ値の検出、正解ラベルの分布の調査、データセットのZスコア標準化を行って、Diabetesデータセットで回帰分析をする準備をしていきます。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
本シリーズと本連載について
本シリーズ「Pythonデータ処理入門」は、Pythonの基礎をマスターした人を対象に以下のような、Pythonを使ってデータを処理しようというときに便利に使えるツールやライブラリ、フレームワークの使い方の基礎を説明するものです。
- NumPy(「NumPy超入門」の目次はこちら)
- pandas(本連載)
- Matplotlib
なお、本連載では以下のバージョンを使用しています。
- Python 3.12
- pandas 2.2.1
前回のまとめ
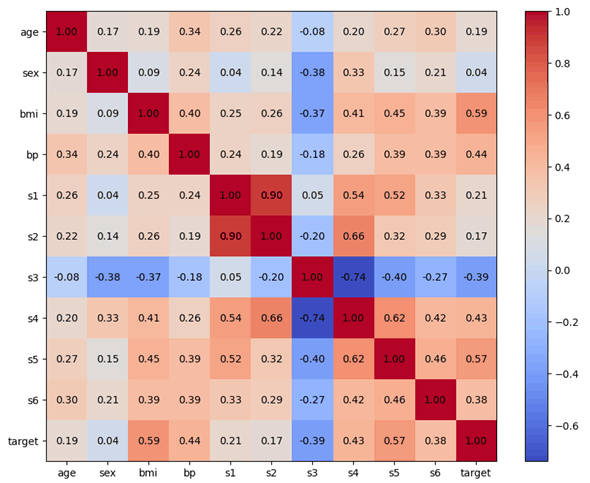
前回は、scikit-learnが提供するDiabetesデータセットを例として、その概要を調べたり、相関係数を計算してヒートマップをプロットしたり、散布図をプロットしたりしながら、target列との相関が強そうな列がどれかを考えてきました。
以下はそのヒートマップです。
このヒートマップからは以下の列がtarget列との相関が0.3以上もしくは−0.3以下であることが確認されました。
- bmi:BMI
- bp:血圧
- s3:善玉コレステロール
- s4:倉庫レストラン値/善玉コレステロール
- s5:中性脂肪
- s6:血糖値
前回の記事では、中でもbmi列とs3列の2列が回帰分析を行う際のモデルの特徴量として、予測精度への寄与度が高い可能性があると考えました。他の列については、予測精度の向上を検討する際に追加するか否かを考えることにしています。
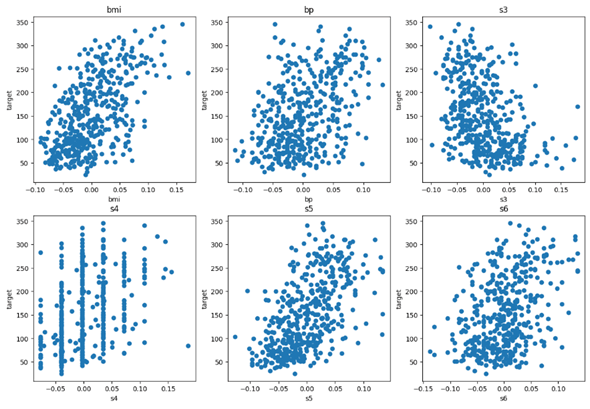
また、これらの列の値を横軸に、target列の値を縦軸にした散布図をプロットしました。それが以下です。
これらの散布図からは各列とtarget列の間に一定の相関が見られます(ただし、s4についてはやや離散的ですが)。
今回は元のデータセットからこれらの列(とtarget列)を抜き出して、その操作を続けていくことにします。というわけで、以下のモジュールをインポートしておきましょう。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
そして、以下のコードでDataFrameオブジェクトを作成しておきましょう(元のデータセットはdf_orgに保存しておきます)。
diabetes = datasets.load_diabetes()
X = diabetes.data
y = diabetes.target
feature_names = diabetes.feature_names
df_org = pd.DataFrame(X, columns=feature_names)
df = df_org.loc[:, ['bmi', 'bp', 's3', 's4', 's5', 's6']]
df['target'] = y
ここでは上でピックアップした列(とtarget列)だけを含むDataFrameオブジェクトを作成し、以下ではそれを扱うことにします(元のデータセットはdf_orgという名前で取っておきます)。
ここからは次のような処理を順にしていくことにしましょう。
- 外れ値をチェックして、DataFrameオブジェクトから削除する
- target列の分布に偏りがないかどうかを確認する
- データセットを標準化する(Zスコア標準化)
外れ値をチェックして、DataFrameオブジェクトから削除
外れ値がデータセットに含まれていると、モデルの学習が不安定になり、予測精度が低下する可能性があります。そこで、まずは外れ値があるかどうかをチェックして、(何らかの値に置き換えるなどの対応も考えられますが)今回は単純にそれらを含む行を削除することにします。
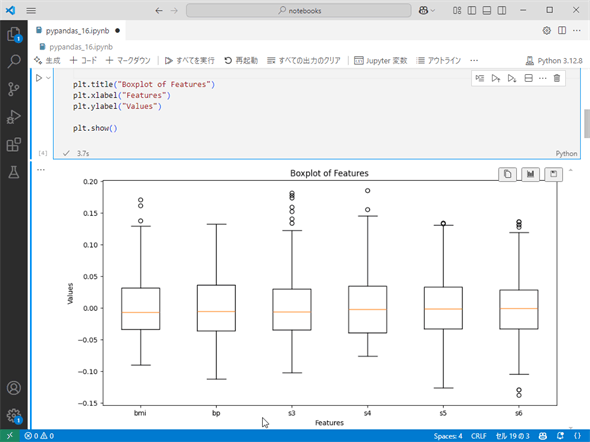
まずは外れ値があるかどうかを可視化してみましょう。
features = df.drop('target', axis=1) # 箱ひげ図にtarget列以外を描画
plt.figure(figsize=(12, 6))
plt.boxplot(features.values, tick_labels=features.columns)
plt.title("Boxplot of Features")
plt.xlabel("Features")
plt.ylabel("Values")
plt.show()
これをVisual Studio Codeで実行した結果が以下です。
箱ひげ図では四分位範囲(第1四分位数=Q1から第3四分位数=Q3の間)が矩形《くけい》(=長方形)として描かれ、その上下端からは四分位範囲(Q3−Q1)を1.5倍した長さを上下に伸ばして髭(ひげ)のように描画しています。この範囲から外れた値を外れ値として見なすのが一般的です。この結果を見ると、bp列を除く全ての特徴量で外れ値が存在しているようです。
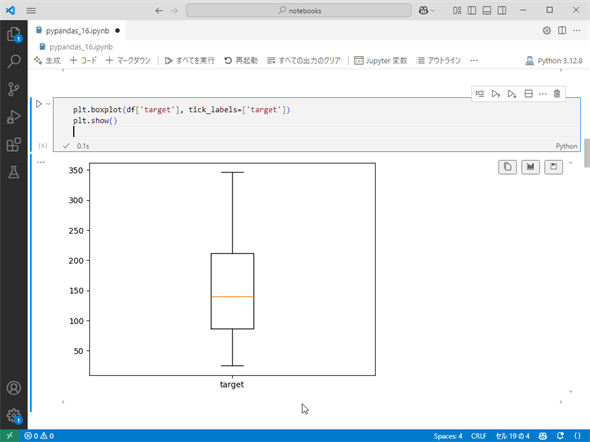
target列についても同じことをしてみます(target列についてはスケーリングされていないことから、縦軸の値が特徴量の列とは大きく異なっているため、別扱いとしています)。
plt.boxplot(df['target'], tick_labels=['target'])
plt.show()
この結果は以下のようになりました。
target列には外れ値が確認されませんでしたが、各特徴量に外れ値があることは視覚的に確認できました。そこで、外れ値を含む行だけで構成されるDataFrameオブジェクトを作成してみます。以下はそのためのコードです。
Q1 = df.quantile(0.25)
Q3 = df.quantile(0.75)
IQR = Q3 - Q1
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR
mask = (df < lower_bound) | (df > upper_bound)
outliers = df[mask.any(axis=1)]
print(f'outliers: {outliers.shape[0]} rows')
outliers
ここでは第1四分位数(Q1)と第3四分位数(Q3)、四分位範囲(IQR)を求めて、そこから外れ値かどうかを判定するしきい値としてlower_bound、upper_boundを計算しています。
次の図のようにIQRの内容を出力してみましょう。これらは単独の値(スカラー値)ではなく、列ごとに特定の値になっていることには注意してください。
そして、下限のしきい値よりも小さい値、もしくは上限のしきい値よりも大きい値を含む行を示すマスクを「mask = (df < lower_bound) | (df > upper_bound)」のようにして計算しています。次の図のようにmaskの内容を出力してみましょう。
次にこのマスクを使って「df[mask.any(axis=1)]」としています。これは、anyメソッドで「いずれかの列でマスクの値がTrueとなっている行」をDataFrameオブジェクトから取り出すことを意味しています。
実行結果を以下に示します。
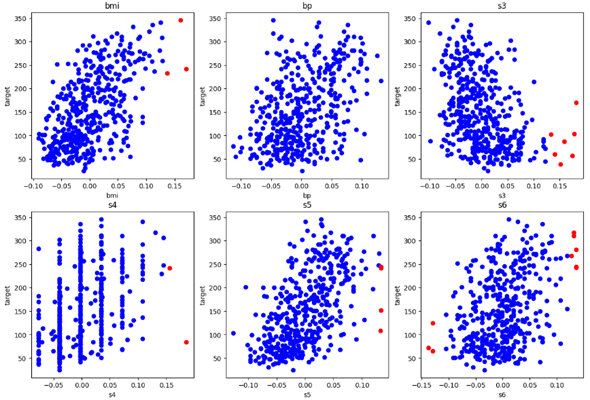
ついでに冒頭で見ていただいた散布図で外れ値が赤でプロットされるようにしてみました。
cols = ['bmi', 'bp', 's3', 's4', 's5', 's6']
fig, axes = plt.subplots(nrows=2, ncols=3, figsize=(15, 10))
axes = axes.flatten()
for n, col in enumerate(cols):
ax = axes[n]
ax.scatter(df.loc[~mask[col], col], df.loc[~mask[col], 'target'], color='blue')
ax.scatter(df.loc[mask[col], col], df.loc[mask[col], 'target'], color='red')
ax.set_title(col)
ax.set_xlabel(col)
ax.set_ylabel('target')
plt.show()
実行結果を以下に示します。
箱ひげ図では外れ値はbmi列とs3〜s6列に見られました。散布図でもそのようになっていることが確認できました。
では、外れ値を含む行を削除しましょう。これには幾つかのやり方があります。以下は先ほど作成したmaskを使うものです。
df_cleaned = df[~mask.any(axis=1)]
print(f'cleaned DataFrame: {df_cleaned.shape[0]} lines')
先ほどは「mask.any(axis=1)」として、外れ値を含む行を取り出していました。今度は「~mask.any(axis=1)」として、その真偽値を反転しています。これにより、外れ値を含まない行だけを取り出すようにしています。
もう1つのやり方を紹介しましょう。こちらはDataFrameオブジェクトのdropメソッドを使います。
df_cleaned_2 = df.drop(outliers.index)
print(f'cleaned DataFrame: {df_cleaned_2.shape[0]} lines')
outliersというDataFrameオブジェクトには、外れ値を含む行だけが格納されています。dropメソッドにそれらのインデックスを与えることで、元のDataFrameオブジェクトからそれらを削除した、新しいDataFrameオブジェクトを作成しています。
どっちがいいのでしょうか? と問われても筆者には判断がつきません。前者はマスクを使っていますが、「真偽値を反転しているところが分かりにくい」とか「外れ値を削除する=外れ値でないものを選択する点が分かりにくい」という人もいるかもしれません。後者は削除する対象をダイレクトに指定しているという点では分かりやすいといえるでしょう。また、後から外れ値について検討したい場合には、それらを含むDataFrameオブジェクトを作成するでしょうからその活用ともいえます。
ということで、以降では外れ値を削除したDataFrameオブジェクトに対して操作していくことにします。
df = df_cleaned
target列の分布に偏りがないかどうかをチェック
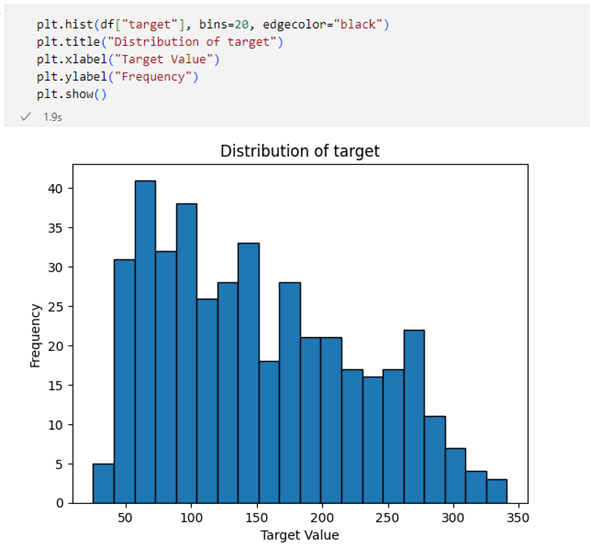
次にtarget列の分布に偏りがないかどうかを確認しましょう。ターゲットが正規分布に従っていなくても回帰分析は適用可能ですが、分布の偏りがないかどうかを確認しておくのは有用です。そこで、target列のヒストグラムをプロットして視覚的に確認してみましょう。
plt.hist(df["target"], bins=20, edgecolor="black")
plt.title("Distribution of target")
plt.xlabel("Target Value")
plt.ylabel("Frequency")
plt.show()
実行結果は以下のようになりました。
一見したところでは、target列の分布は正規分布とは異なる形をしています。そこで、数値的にどの程度の偏りがあるかを確認してみましょう。これにはDataFrame.skewメソッドとDataFrame.kurtosisメソッドを使います。前者はデータ分布の歪度(わいど、skewness)を調べるために使い、後者はデータの尖度(せんど、kurtosis)を調べるために使います。
歪度と尖度はともにデータセットの分布の偏りや形状を示す指標として使われます。これらのうち、歪度は分布に対する左右の非対称性(=ゆがみ)を表します。例えば正規分布のように左右対称であれば(視覚的には左右に等しく裾野が広がっていれば)、skewメソッドの戻り値は0(に近い値)になります。右に裾野が広がっている分布であれば戻り値は正数に、左に裾野が広がっているような分布であれば戻り値は負数になります。
尖度は分布のとがり具合を示します。基準値が0の場合、分布の形状が正規分布に近い可能性があります(基準値を3とする解釈もあります。pandasのDataFrame.kurtosisメソッドは正規分布に対しては0を返します)。それより大きな値であればよりとがった分布になっていることを示し、それより小さな分布では平べったい分布であることを示します。
試してみましょう。
print('skewness:', df['target'].skew())
print('kurtosis:', df['target'].kurt())
実行結果を以下に示します。
歪度は0.435程度となりました。これは右側に裾野が広がるような分布であることを示しています(先ほどの画像を見るとそのようになっていますね)。尖度は-0.876程度です。これは、どちらかといえば平べったい分布になっていることを示しています。
歪度と尖度は分かったのですが、問題はtarget列の分布を偏りが少ないものと考えてそのまま使ってもよいか、それとも何らかの修正が必要かです。一般的には歪度も尖度も「その絶対値が0.5以内であれば偏りが小さい」と見なせます。「その絶対値が0.5〜1.0の範囲であれば、必要に応じて修正を検討する」ことになります。それ以上であれば修正が必要になる可能性が高いです。
歪度の0.435という値は偏りが小さいと見なせそうです。尖度の-0.876という値については状況によっては修正が必要となります。が、今回はそのままにしておくことにしました。
平均0、標準偏差1となるようにスケーリング
前回にも述べましたが、Diabetesデータセットでは「平均が0、ユークリッドノルム(L2ノルム)が1、つまりsum(x2)=1)に正規化された値となって」います。ここでは、これを「平均0、標準偏差1」となるようにスケーリングしてみます(このようなスケーリングのことをZスコア標準化などと呼ぶこともあります)。
ここでは以下の方法でこれを求めます。
- 各列の標準偏差を求めて、各値を標準偏差で除算する
詳細は「AI・機械学習の用語辞典」の「正規化/標準化とは?」を参照していただくものとして、以下の式を見てください。
ここで、x'はスケーリング後の各列の値、xはスケーリング前の各列の値、ハット付きのxは平均値、σは標準偏差を表しています。要するに、各列の各値と平均値の差分を標準偏差で除算すれば、平均値が0で標準偏差が1のデータセットに標準化できるということです。
というわけで、今述べたように「各列の各値と平均値の差を標準偏差で除算する」ことで、平均値が0、標準偏差が1となるようにしてみましょう。その前に現在の標準偏差も確認しておきます。
print(df_cleaned.std(ddof=0))
実行結果を以下に示します。
平均0、標準偏差1のデータセットになるようにスケーリングするコードを以下に示します(ここではtarget列をスケーリングの対象から外しています)。
df_standardized = df.copy()
df_standardized = df_standardized.drop(['target'], axis=1)
std = df_standardized.std(ddof=0)
df_standardized = (df_standardized - df_standardized.mean()) / std
これで標準偏差が1になったかどうかを確認します。
print(df_standardized.std(ddof=0))
実行結果を以下に示します。
確かに標準偏差が1になりました。
今回は外れ値の発見と削除、target列の分布に偏りがないかどうかの確認、Zスコア標準化といった処理をしてきました。次回は、このデータセットを使って回帰分析を行い、その評価をしてみます。
最後にいろいろと修正を加えたデータセットをCSVファイルに保存しておきましょう(標準化の前に落としていたtarget列を足しています)。
df_standardized['target'] = df['target']
df.to_csv('diabetes.csv', index=False)
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ

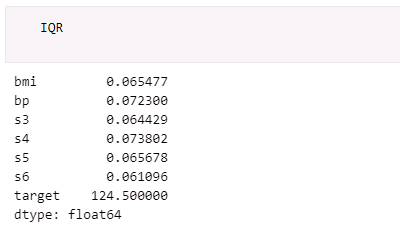 IQRは列ごとの四分位範囲を含んでいる
IQRは列ごとの四分位範囲を含んでいる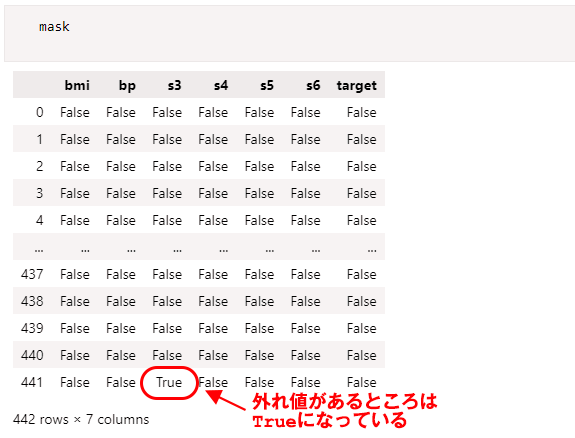 s3列の441行目がTrueになっている点に注目
s3列の441行目がTrueになっている点に注目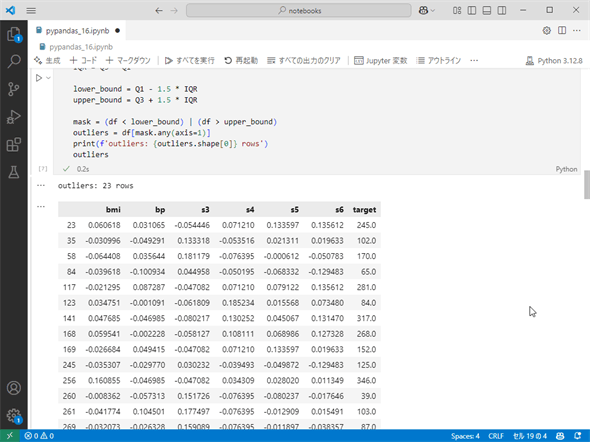
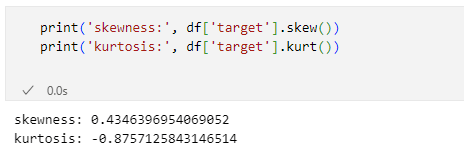 歪度の0.435は右に裾野が広がることを、尖度の-0.88はそれほど尖っていないことを示している
歪度の0.435は右に裾野が広がることを、尖度の-0.88はそれほど尖っていないことを示している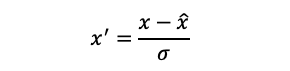
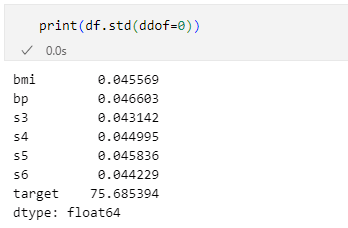 標準偏差が1ではないことを確認
標準偏差が1ではないことを確認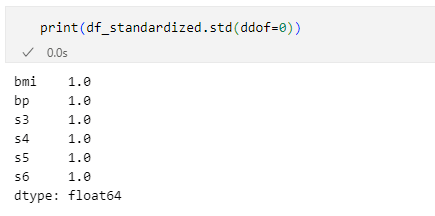 標準偏差が1になった
標準偏差が1になった



