[pandas超入門]Diabetesデータセットを使って回帰分析してみよう(単回帰分析編):Pythonデータ処理入門
Diabetesデータセットから特徴量としてBMIを選択して、単回帰分析を行ってみます。単回帰分析でうまくターゲットを予測できるのかどうかを見ていきましょう。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
本シリーズと本連載について
本シリーズ「Pythonデータ処理入門」は、Pythonの基礎をマスターした人を対象に以下のような、Pythonを使ってデータを処理しようというときに便利に使えるツールやライブラリ、フレームワークの使い方の基礎を説明するものです。
- NumPy(「NumPy超入門」の目次はこちら)
- pandas(本連載)
- Matplotlib
なお、本連載では以下のバージョンを使用しています。
- Python 3.12
- pandas 2.2.1
前回のまとめ
前回は、scikit-learnが提供するDiabetesデータセットを例として、外れ値の発見と除去、target列の分布に偏りがないかどうかの確認、Zスコア標準化(平均0、分散1となるようにデータをスケーリング)しました。
今回はそのときに保存したデータセットを使って単回帰分析を行ってみます。なお、データセットには以下の列が含まれていることを思い出してください。これらは前々回にDiabetesデータセットを視覚化した際にtarget列と相関が比較的強かった列です。
- bmi:BMI
- bp:血圧
- s3:善玉コレステロール
- s4:倉庫レストラン値/善玉コレステロール
- s5:中性脂肪
- s6:血糖値
中でもbmi列(BMI)とs3列(善玉コレステロール)の2列はtarget列との相関が特に高いため、回帰分析を行う際のモデルの特徴量として優先的に使用することとしました。他の列については、予測精度の向上を検討する際に追加するか否かを考えることにしています。
まずは以下のコードでpandasやNumpy、Matplotlibをインポートし、前回に保存したデータセットを読み込みます。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
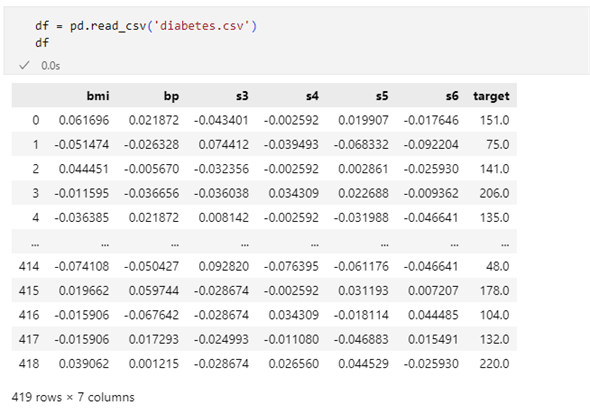
df = pd.read_csv('diabetes.csv')
df
以下はVisual Studio Codeでこのコードを実行した結果です。
回帰分析とは
回帰分析とは何らかの変数の値を基に、それとはまた別の変数の値を予測する手法のことです。基となる変数を特徴量とか説明変数と呼びます。また、予測する変数のことをターゲットとか目的変数と呼びます。特徴量とターゲットはどちらかというと機械学習の世界でよく使われ、説明変数と目的変数は数学(統計学)の世界でよく使われます。今話題にしているDiabetesデータセットではtarget列を除く他の列が特徴量(説明変数)で、target列がターゲット(目的変数)に相当します。
そして、1種類の特徴量(説明変数)を用いてターゲット(目的変数)の値を予測することを単回帰分析といいます(複数の特徴量を用いてターゲットの値を予測することは重回帰分析と呼びます。これについては次回以降に取り上げる予定です)。
回帰分析では、特徴量とターゲットの関係は一般的には一次式の形で表されます。単回帰分析なら特徴量をx、ターゲットをy、回帰係数(傾き)をw、切片をbとした「y=wx+b」のような形です。そして、データセットを用いて学習することで、データセットに含まれるデータの分布を最もよく表すwとbを求めます。学習の際には、最小二乗法などの手法が用いられます。
また、上で述べた「y=wx+b」という一次式は、特徴量とターゲットの関係を表すモデルともいえます。逆にいえば、回帰分析(線形回帰)では特徴量とターゲットの関係を一次式の形でモデル化すると表現できるでしょう。
Pythonを使って自分の手で回帰分析を行うコードを書くのはなかなか骨が折れるかもしれません。が、scikit-learnには、回帰分析を行うためのLinearRegressionクラスが用意されているので、実はコードは簡単です。以下ではこのクラスを使って単回帰分析をしてみましょう。大まかな手順は次の通りです。
- データセットを訓練データとテストデータに分割
- モデルの作成
- 訓練データを使った学習
- テストデータを使ったモデルの評価
手順に従って単回帰分析する前に、後で使う以下の関数とクラスをインポートしておいてください。
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
データセットの分割
先ほど読み込んだデータセットは、まずモデルの学習(train)用とテスト(test)用に分割しておきます(「train」に使うデータということで、ここでは「訓練データ」と記述することにします)。訓練データは、モデルが最適なwとbを求めるために使われます(このときに最小二乗法などが用いられますが、これはLinearRegressionクラスの内部で行われることなので、自分でそのコードを書く必要はありません)。そして、学習後のモデルは「未知のデータ」に対しても適切な結果を予測できるかどうか、つまり、学習に使っていないデータを与えたときにモデルがどれだけ正確な予想をできるかどうか(これを「汎化性能」と呼びます)を検証するために使われます。
データセットを分割するにはscikit-learnが提供するtrain_test_split関数を使います(sklearn.linear_modelモジュール)。
train_test_split関数は、引数として与えたNumPy配列やリスト、DataFrameオブジェクトを訓練データとテストデータに分割します。主要なパラメーターを以下に示します。
- test_sizeパラメーター:浮動小数点数値または整数値を指定。浮動小数点数値を指定した場合は、テストデータの割合が指定されたと解釈され、整数値を指定した場合は、テストデータを構成する行数が指定されたと解釈される(指定しなかった場合は0.25が指定されたものと見なされる。つまり、データセットの4分の1がテストデータになる)。同様に訓練データの割合または行数を指定するtrain_sizeパラメーターもあるが、ここでは使用しない(この場合、test_sizeパラメーターに従って分割されたデータの残りが訓練データとなる)
- random_stateパラメーター:任意の整数値を指定。データセットをシャッフルする(ランダムに分割する)際のシードの指定。同じ値を指定すると、常に同じようにシャッフルされるので、シャッフルの再現性を確保できる。データセットをシャッフルするかどうかは、shuffleパラメーターで指定する
- shuffleパラメーター:TrueかFalseを指定。Trueならシャッフルし、Falseならシャッフルしない(デフォルト値はTrue)
実際のコードは以下の通りです。ここでは特徴量('bmi'列)とターゲット('target'列)を別々のDataFrameオブジェクトに分け、それらをtrain_test_split関数で分割しています。test_sizeパラメーターには0.2を指定し(全データセット20%がテストデータに、残りの80%が訓練データ)、shuffleパラメーターの指定は省略します(シャッフルする)。random_stateパラメーターが765になっているのは、筆者がナムコ好きだからで、それ以上の意味はありません。
X = df[['bmi']]
y = df[['target']]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=765)
print(f"train data: {X_train.shape}, {y_train.shape}")
print(f"test data: {X_test.shape}, {y_test.shape}")
以下に実行結果を示します。
訓練データが335行、テストデータが84行なので、総データ数の20%が確かにテストデータになっていることが分かりました。
上のコードを見て「戻り値を4つの変数に代入しているのはなぜ!」と思うかもしれません。特徴量を2つのデータセットに分割し、ターゲットを2つのデータセットに分割するのでそうなってしまうのです。その用途は次の通りです(なお、Xが大文字で、yが小文字なのは、機械学習や統計学のモデルを数学的に表現する際、行列は大文字の変数で、ベクトル(あるいはスカラー)は小文字の変数で表すのが一般的ですが、その慣習をそのままコードにも適用しているためです)。
- X_train:学習で使用する特徴量
- X_test:テストで使用する特徴量
- y_train:学習で使用するターゲット
- y_test:テストで使用するターゲット
次にモデルの作成と学習に進みましょう。
モデルの作成と学習
モデルの作成といっても特に難しいことはありません。先ほどインポートしたLinearRegressionクラスのインスタンスを作成するだけです。学習もカンタン。そのfitメソッドに訓練データ(特徴量とターゲットの両者)を渡すだけです。
model = LinearRegression()
model.fit(X_train, y_train)
print(f'coef: {model.coef_}')
print(f'intercept: {model.intercept_}')
最後の2行のprint関数呼び出しは、回帰係数(傾き)と切片を出力するコードです。LinearRegressionクラスでは回帰係数はcoef_属性で、切片はintercept属性で取得できます。
この画像を見ると、傾きが900程度、切片が151くらいと驚くほど大きな数字になっているのが分かります。これは'target'列を標準化(Zスコア標準化)していないからです。
モデルとテストと決定係数
これだけのコードで単回帰分析ができてしまいました。次にこのモデルのpredictメソッドにテストデータ(特徴量)を渡して予想してもらいましょう。
y_pred = model.predict(X_test)
予測結果はy_predに代入しておきます。そうしたら、これをテスト用のターゲットと比較して、このモデルの回帰式(先ほど見た回帰係数と切片を使って「予測値=回帰係数×特徴量+切片」と記述できます)を使った予測が、ターゲットの値(とは、実際に観測されたデータのことです)にどの程度当てはまっているかを検証します。このときには「決定係数」(coefficient of determination)を計算する関数が一般的によく使われます。
決定係数は「R2」とも表記されます。上でも述べたように、モデルが予測した値がターゲット(観測値)にどれくらい当てはまっているかを示す値といえます。その値は以下の式で計算されます。
日本語で書くと「(ターゲットの値−予測値)を二乗したものの総和」(残差平方和)を「(ターゲットの値−ターゲットの平均)を二乗したものの総和」(全平方和)で除算したものを1から減算した値となります。通常、これは0から1の値を取り、その値が1に近いほど、モデルによる予測がターゲットによく当てはまっているといえます。
R2の値はだいたい次のように解釈できます(ただし、分野によってはR2が低くても有益なモデルとされることもあります)。
- R2=1:完全に当てはまっている(理想的)
- 0.8<R2<1.0:かなりよい
- 0.5<R2<0.8:まあまあよい
- 0.3<R2<0.5:それほど高くはないが最悪でもない
- R2<0.3:よくない
と難しいことを書いても、やることは簡単で先ほどインポートしたr2_score関数にテストデータ(ターゲット)と予測結果(y_pred)を渡すだけです。
r2 = r2_score(y_test, y_pred)
print(f'r2: {r2}')
あるいはLinearRegressionクラスのscoreメソッドにテストデータ(ターゲット)と予測結果(y_pred)を渡しても同じ結果が返されます。
score = model.score(X_test, y_test)
print(f'score: {score}')
これを実行した結果を以下に示します。
この結果からはこのモデルではR2は0.42くらいであることが分かりました。1に近づくほど、ターゲット(実際に観測されたデータ)に対する、このモデルの予測値の当てはまり度が高いことは既に述べた通りですが、ではこの0.42という値はどうなのでしょうか。R2の値は0.5を超えればまあまあよいモデルといえます。0.8を超えればかなりよいモデルです。0.3〜0.5は精度としてはそれほど高くないでしょう。それ以下は精度が低いと考えられます。
ということで、0.42という値からは、このモデルは「データの分布のばらつきをある程度は説明できるけど、それほど高くはない」といえます。今回は1つの特徴量だけを使ったモデルなので、特徴量を増やして重回帰分析を行えばもっとよいモデルになるかもしれませんし、残差分析と呼ばれる手法を使ってこのモデルの予測値とターゲットの値との差異を詳細に分析することも可能でしょう。ただし、ここではそこまでは踏み込まないことにします。
結果をプロットしてみる
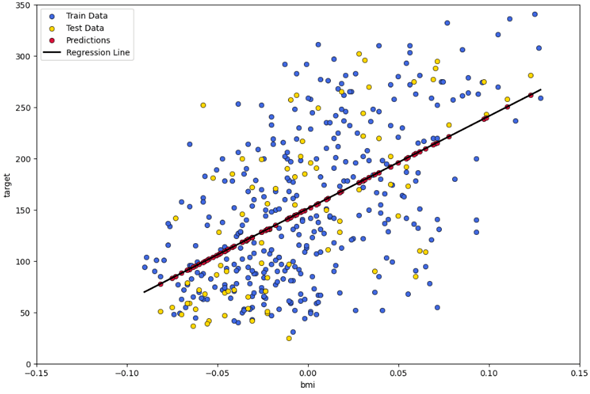
では、今までの結果を散布図としてプロットしてみましょう。横軸がBMIで縦軸が1年後の進行度合いを示す値です。
- 青い点:訓練データ
- 黄色い点:テストデータ(実測値)
- 赤い点:予測値
- 黒い実線:今回のモデルの回帰係数と切片を使ったグラフ
プロットするコードは次の通りです(詳しい説明は省略します)。
plt.figure(figsize=(12, 8))
plt.scatter(X_train, y_train, color='royalblue', label='Train Data',
edgecolors='black', linewidth=0.5)
plt.scatter(X_test, y_test, color='gold', label='Test Data',
edgecolors='black', linewidths=0.5)
plt.scatter(X_test, y_pred, color='crimson', label='Predictions',
edgecolors='black', linewidth=0.5)
X_line = np.linspace(X.min(), X.max(), 100)
y_line = model.intercept_[0] + model.coef_[0, 0] * X_line
plt.plot(X_line, y_line, color='black', label='Regression Line', linewidth=2)
plt.xlim(-0.15, 0.15)
plt.ylim(0, 350)
plt.xlabel('bmi')
plt.ylabel('target')
plt.legend()
plt.show()
実行結果を以下に示します。
このグラフからは次のようなことが読み取れます。
- 直線が右肩上がりであることから、BMIと糖尿病の進行の度合いにはある程度の正の相関があると考えられる
- 予測値は回帰式を基に計算されるので、赤い点が回帰直線上に並ぶのは正しい
- ただし、予測値とターゲット(実測値。青い点と黄色い点)の間に乖離《かいり》(誤差)がある。これはモデルの実測値に対する当てはまり度が低いことを意味している(単回帰モデルではターゲットを正確に予測するのは難しい)
- 青い点(訓練データ)と黄色い点(テストデータ)の分布はバランスが良く、極端な語りは見られない。このことから、データセット分割時のシャッフルはうまくいっていると考えられる
これまでの処理を関数にまとめておく
最後にこれまでに行ってきた処理を関数にまとめておきます。次回もこれらを使う予定です(自作モジュールにまとめるわけではないので、Jupyter Notebookからコピー&ペーストすることになりますが)。
def split_data(df, rows=None, rs=765):
if rows is None:
rows = ['bmi']
X = df[rows]
y = df[['target']]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=rs)
return X_train, X_test, y_train, y_test
def fit_and_predict(model, X_train, y_train, X_test, y_test):
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
r2 = r2_score(y_test, y_pred)
return r2, y_pred
def plot_data(model, X_train, y_train, X_test, y_test, y_pred):
plt.figure(figsize=(12, 8))
plt.scatter(X_train, y_train, color='royalblue', label='Train Data',
edgecolors='black', linewidth=0.5)
plt.scatter(X_test, y_test, color='gold', label='Test Data',
edgecolors='black', linewidths=0.5)
plt.scatter(X_test, y_pred, color='crimson', label='Predictions',
edgecolors='black', linewidth=0.5)
X_line = np.linspace(X.min(), X.max(), 100)
y_line = model.intercept_[0] + model.coef_[0, 0] * X_line
plt.plot(X_line, y_line, color='black', label='Regression Line', linewidth=2)
plt.xlim(-0.15, 0.15)
plt.ylim(0, 350)
plt.xlabel('bmi')
plt.ylabel('target')
plt.legend()
plt.show()
ここでデータセット分割時のrandom_stateパラメーターの値を変えて、これまでと同じことをしてみましょう。
X = df[['bmi']]
y = df[['target']]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=573)
model = LinearRegression()
r2, y_pred = fit_and_predict(model, X_train, y_train, X_test, y_test)
print(f'r2: {r2}')
実行結果を以下に示します。
なんと、同じデータセットを使っていても、データ分割のやり方を変えるだけでR2が大きく低下してしまいました。これはそもそもデータ数が少な過ぎるのが一番大きな原因と考えられます。データ数が少ないために、データ分割により訓練データとテストデータの分布などに偏りが発生したのかもしれません。クロスバリデーション(交差検証)を行うことで改善する可能性もありますが、本記事は『pandas超入門』というコンセプトなので深追いせずに次に進むことにします。
というわけで、次回はより精度の高いモデルを作るべく重回帰分析に挑戦してみます。
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ


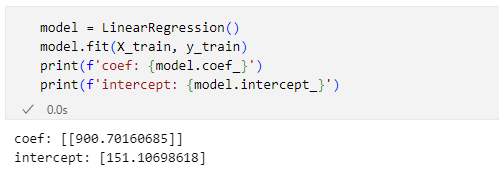 LinearRegressionクラスのインスタンス生成と学習、回帰係数と切片の出力
LinearRegressionクラスのインスタンス生成と学習、回帰係数と切片の出力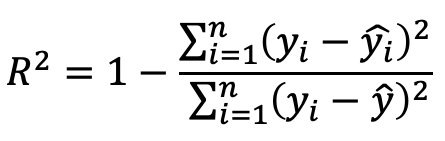 R2を計算する式
R2を計算する式 R2は「0.42」程度
R2は「0.42」程度