［評価関数］相対絶対誤差（RAE：Relative Absolute Error）／相対二乗誤差（RSE：Relative Squared Error）とは？：AI・機械学習の用語辞典

用語「相対絶対誤差」「相対二乗誤差」について説明。相対絶対誤差は、平均絶対誤差を平均絶対偏差（＝データの広がり具合）で割ることでスケールを調整（＝相対化）した評価値を表す。相対二乗誤差は、平均二乗誤差を分散（＝データの広がり具合）で割ることでスケールを調整（＝相対化）した評価値を表す。

[一色政彦，デジタルアドバンテージ]

連載目次

用語解説

　統計学／機械学習における相対絶対誤差（RAE：Relative Absolute Error）とは、平均絶対誤差（MAE）を平均絶対偏差（MAD）（＝データ／観測値の広がり具合、厳密には「平均値」からのバラツキ具合）で割ることで、スケール（単位）を調整（＝正規化）した評価値、またはそれを出力する関数である。絶対誤差を相対的な値に変換したものといえる。このようにすることで、スケールが異なる教師ラベルを含むデータ間でも評価値の比較がしやすくなるというメリットがある。

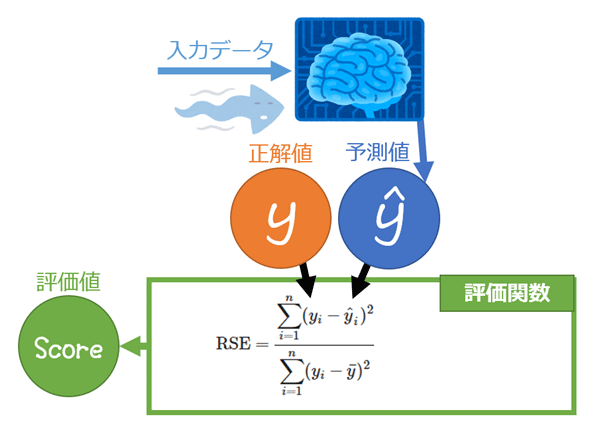
　同様に、相対二乗誤差（RSE：Relative Squared Error）とは、平均二乗誤差（MSE）を分散（＝データ／観測値の広がり具合）で割ることで、スケールを調整した評価値、またはそれを出力する関数である。その評価値は、二乗誤差を相対的な値に変換したものといえる。メリットは先ほどと同じだ。

図1　相対絶対誤差／相対二乗誤差のイメージ

用途

　相対絶対誤差／相対二乗誤差を評価指標としてう使う場面を（筆者の経験では）あまり見ることはないが、Azure Machine Learningでは回帰モデルの評価指標の一つとして出力されるため、用語の一つとして紹介した。

　その用例のように、主に線形回帰などの評価関数として用いられる。0に近いほど誤差が小さいことになるので、精度／性能が良いことを意味する。いずれも0.0〜1.0＝100％が基本的な評価値の幅となるが、誤差が大きい場合は当然、1.0を超えることもある。

　機械学習において、評価値を相対的な値に変換して出力する評価関数には、

• 平均絶対パーセント誤差（MAPE：Mean Absolute Percentage Error）
• 平均二乗パーセント誤差の平方根（RMSPE：Root Mean Squared Percentage Error）

もあり、通常はこれらを使うケースの方が多いのではないかと思う。例えばscikit-learnでは、平均絶対パーセント誤差（MAPE）を計算するmean_absolute_percentage_error()関数は用意されているが、相対絶対誤差を計算する評価関数は用意されていない。

「相対絶対誤差」の定義と数式

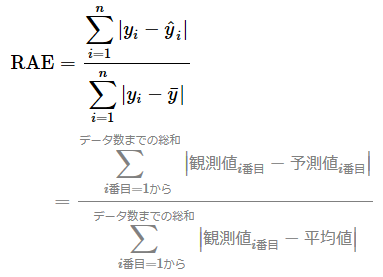
　相対絶対誤差（RAE）の数式は、次のようになる。統計学に寄せて「観測値（observed value）」と表記したが、「実測値」「実際の測定値」の他、さまざまな方法で収集したデータがこの対象となる。

　平均絶対誤差（MAE）を平均絶対偏差（MAD）で割る式ではあるが、平均（1/n）の分母と分子は消せるので、厳密には絶対誤差の総和を絶対偏差の総和で割った式になる。

「相対二乗誤差」の定義と数式

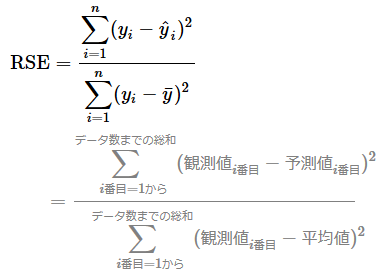
　相対二乗誤差（RSE）の数式は、次のようになる。

　平均二乗誤差（MSE）を分散で割る式ではあるが、平均（1/n）の分母と分子は消せるので、厳密には二乗誤差の総和を二乗偏差の総和で割った式になる。

　この計算式を見ると気付くが、R²＝1−RSEとなる点に注目してほしい。つまり決定係数R²は、相対二乗誤差（RSE）の符号を反転させて1から引くことで、1.0（＝100％）に近いほど良い精度となる計算式に調整したものであり、両者は同じものを表す評価指標といえる。

「AI・機械学習の用語辞典」