[pandas超入門]データをスケーリングしてみよう(正規化と標準化):Pythonデータ処理入門
データのスケーリング、正規化、標準化とはどんな処理なのか、その違いは何かなどを簡単なDataFrameオブジェクトを例に見ていきましょう。
この記事は会員限定です。会員登録(無料)すると全てご覧いただけます。
本シリーズと本連載について
本シリーズ「Pythonデータ処理入門」は、Pythonの基礎をマスターした人を対象に以下のような、Pythonを使ってデータを処理しようというときに便利に使えるツールやライブラリ、フレームワークの使い方の基礎を説明するものです。
- NumPy(「NumPy超入門」の目次はこちら)
- pandas(本連載)
- Matplotlib
なお、本連載では以下のバージョンを使用しています。
- Python 3.12
- pandas 2.2.1
前回はヒストグラムの描画とDataFrameオブジェクトのビニングを試してみました。今回はデータのスケーリングについて見てみましょう。その前にpandasをインポートしておきます。
import pandas as pd
データのスケーリングとは
データのスケーリングとは、データを一定の基準に合わせて使いやすくなるように変換することです。大きな整数値と小数点以下の値に意味がある実数値などが、あるデータセットに混在していた場合、データセットからのモデルの訓練過程や訓練済みモデルの性能に、それらの値の大小が影響を及ぼすことがあります。そうではなく、何らかの基準に従うようにデータを変換し、一定の形式に整えることでそうした影響を抑えられるでしょう。といっても言葉では分かりにくいので、これについては後で実際に試してみましょう。
スケーリングにもいろいろな種類がありますが、今回は以下の2つを取り上げます。
- 正規化:最小値0、最大値1の範囲に収まるようにデータをスケーリングする
- 標準化:平均0、標準偏差1の範囲に収まるようにデータをスケーリングする
なお、正規化と標準化という呼び方は「AI・機械学習の用語辞典」の「正規化(Normalization)/標準化(Standardization)とは?」に合わせたものです。詳細については前掲のリンクを参照してください。
また、Titanicデータセットの話に入る前に、ここでは以下のDataFrameオブジェクトを使って、正規化と標準化を試してみます。
ages = [20, 10, 40, 50, 30]
heights = [176, 110, 168, 180, 172]
weights = [68, 28, 72, 85, 58]
d = {'Age': ages, 'Height': heights, 'Weight': weights}
tmp = pd.DataFrame(d, index=['A', 'B', 'C', 'D', 'E'])
tmp
コードを見れば内容は把握できるでしょうが、作成したDataFrameオブジェクトは次のようになります。
以下ではこのDataFrameオブジェクトを使って、データセットの正規化と標準化をしてみましょう。
正規化
既に述べましたが、ここでいう正規化(Normalization)とは、以下のような形にデータを変形(スケーリング)することを指します。
- 最小値0、最大値1の範囲に収まるようにデータを変形する
上のDataFrameオブジェクトを例に取れば、その'Age'列は最小値であるB行の10が0に、最大値であるD行の50が1に変形されるということです(その他の値はこれに比例する形で変換されます)。
具体的にはある列のデータに着目して、(特定のデータの値−最小値)を(最大値−最小値)で除算することで変換できます。これをMin-Max normalizationと呼ぶこともあります。
'Age'列について考えてみましょう。この列の個々のデータについて今の計算を当てはめると次のようになります。
この計算を行う関数をここでは「min_max_normalize関数」として次のように定義します。
def min_max_normalize(x):
x_min = x.min()
x_max = x.max()
return (x - x_min) / (x_max - x_min)
とてもシンプルな関数になっているのは、NumPy同様、pandasでもユニバーサル関数(2次元の配列を直観的に扱える関数)がサポートされているからです。上のコードは普通のPythonの関数として定義していますが、これにDataFrameオブジェクトを渡せば列ごとに正規化した結果が得られます。なお、minメソッドは最小値を、maxメソッドは最大値を求めるメソッドです。最後の行はこれを基に正規化した値を計算して、それを戻り値としています。
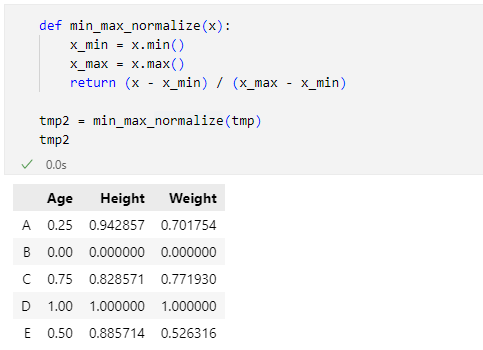
これを呼び出すには次のようにすればよいでしょう。
tmp2 = min_max_normalize(tmp)
tmp2
すると、次のようなDataFrameオブジェクトが得られます。
ここでは自前で正規化を行うmin_max_normalize関数を定義しましたが、scikit-learnにはこれを行う関数(およびクラス)があります。ここではminmax_scale関数を使って、同じことをしてみましょう(scikit-learnをインストールしていない場合は「pip install scikit-learn」「py -m pip install scikit-learn」などのコマンドを実行して、これをインストールする必要があります)。
from sklearn.preprocessing import MinMaxScaler, minmax_scale
a = minmax_scale(tmp)
print(type(a))
print(a)
その結果は以下の通りです。
出力の1行目を見ると分かる通り、minmax_scale関数が返すのはNumPyのndarrayになる点には注意が必要です。DataFrameオブジェクトが必要であれば、pandas.DataFrame関数でDataFrameオブジェクトを作成してください。小数点以下の深いところまでいくと微妙に値が異なるデータもありますが、これは表示桁数の精度の問題で実際にはほぼ同一の値が得られています。
では実際に最小値0、最大値1の範囲に正規化されているかをdescribeメソッドで確認してみます。
出力の中でmin行とmax行を見ると、確かに最小値が0に、最大値が1になっていることが確認できました。
注意が必要な点としては、データセットの中に外れ値が含まれていた場合、それが正規化の際に最小値や最大値として0または1に変換されてしまう可能性が挙げられます。そのため、正規化する前にはそうしたデータがあれば何らかの形で対処する必要があるでしょう。
正規化(Min-Max Normalization)がどんなものかを見たところで、次は標準化について見てみましょう。
標準化
標準化(Standardization)についても既に述べていますが、これは次のような形にデータをスケーリング(変形)することを指します。
- 平均0、標準偏差1の範囲に収まるようにデータを変形する
具体的にはある列のデータに着目して、(特定のデータの値−平均値)を標準偏差で除算することで変換できます。先ほどと同様に、'Age'列について考えてみましょう。ただし、その前に平均値と標準偏差を求めておく必要があります。これには次の画像に示すように、meanメソッドとstdメソッドを使います。
'Age'列の平均値は30.0、標準偏差は15.811として、計算した結果を以下に示します(pandasなどはより高い精度で計算するので、プログラムの出力とは細かなところで違っている可能性はあります)。
上と同様に、ここでも関数を定義しましょう。ここでは関数名は単純に「standardize」としました。
def standardize(x):
std = x.std()
mean = x.mean()
return (x - mean) / std
この関数もシンプルで、標準偏差と平均値を求め、そこから各データを標準化したDataFrameオブジェクトを返送しています。これを呼び出すには次のようにします。
tmp3 = standardize(tmp)
tmp3
実行結果は次の通りです。
だいたい同じような結果になりました。というわけで、次はscikit-learnが提供する標準化を行うscale関数でその結果を比較してみましょう。
from sklearn.preprocessing import scale
tmp4 = scale(tmp)
tmp4 = pd.DataFrame(tmp4, columns=tmp.columns, index=tmp.index)
tmp4
実行結果を以下に示します。
だいたい同じ結果に……なっていませんね! これはどういうことでしょう(わざとらしい)。一口に標準偏差と言っていましたが、実はDataFrameオブジェクトのstdメソッドではデフォルトで「不偏標準偏差」と呼ばれる値を計算しています。これに対して、scikit-learnのscale関数では標準化に当たって、「不偏」が付かない「標準偏差」(あるいは「標本標準偏差」)を用いています。これが2つの実行結果の差を生み出した原因です。
標準偏差と不偏標準偏差について深入りをすると大変なことになるので、ここでは以下のようにまとめるだけとして、詳細は「やさしいデータ分析」の「分散/標準偏差 〜 給与の格差ってどれぐらい?」を参照していただくことにしましょう。
- 標準偏差:データセットに含まれるデータ(標本または母集団)のばらつきをそのまま計算した値。データセットが母集団を網羅しているのであれば、これが母集団の標準偏差となる。データセットが母集団を網羅していないのであれば、これはデータセットに含まれるデータのばらつきを示すだけのものである。このとき、母集団の標準偏差は不偏標準偏差として推定する必要がある
- 不偏標準偏差:データセットが母集団を網羅していない場合に、そこに含まれるデータ(標本)を基にその母集団全体の標準偏差を推定したもの
なるほど。これだけ書いても分からないですよね(くれぐれも詳細については前掲のリンクを参照してください)。これらの計算という面に話を絞ると、標準偏差とはデータセットに含まれる個々のデータと平均値の差を二乗して、それらを合計した値をデータの個数Nで割ったものの平方根です。これに対して、不偏標準偏差はデータの総数をNとしたときに、標準偏差の計算ではNで除算するところを、N−1で除算するのが一般的です。
例えば、これまでに扱ってきたDataFrameオブジェクトの'Age'列で標準偏差と不偏標準偏差を計算すると以下を計算することになります。
実際にこれらをPythonで手計算してみましょう。
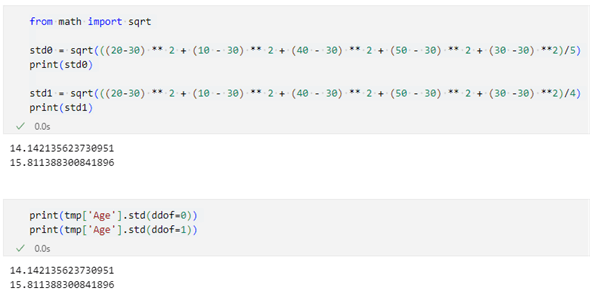
from math import sqrt
# 標準偏差を求める(N=5で除算)
std0 = sqrt(((20 - 30) ** 2 + (10 - 30) ** 2 + (40 - 30) ** 2 + (50 - 30) ** 2 + (30 -30) **2)/5)
print(std0)
# 不偏標準偏差(N−1=4で除算)
std1 = sqrt(((20 - 30) ** 2 + (10 - 30) ** 2 + (40 - 30) ** 2 + (50 - 30) ** 2 + (30 -30) **2)/4)
print(std1)
ちなみに、DataFrame.stdメソッドで標準偏差を計算する際には、ddofパラメーターに「自由度の差分」(Delta Degrees of Freedom)を指定することで、このデータセット(母集団)に含まれるデータ(標本)の標準偏差を計算するのか(ddof=0)、データに基づいて不偏標準偏差を計算するのか(ddof=1)を指定できます(デフォルト値は1)。
ここでいう自由度とは、標準偏差を計算する上で、他のデータとは独立して(自由に)値を取れるデータの数のことです。ここで計算するのが不偏標準偏差の場合、そのデータセットに含まれるデータの平均が計算に使われることから、データのうちの1個は他のデータに依存して決定されることになります。
例えば、'Age'列のデータが[15, 25, 5, 30, ?]という5要素で、その平均が30.0だったとすると、最後のデータ「?」は他のデータとの兼ね合いから(平均値を30.0にするために)75でなければなりません。つまり、自由度(自由に値を取れるデータの数)が1つ減るということです。そして、この減った「1」が自由度の差分(ddof)に当たります。
なお、統計学においても自由度は少し難しい概念です。今回は「そういうものがある」と認識しておくだけでも問題ありません。「やさしいデータ分析」のカイ二乗分布の回で自由度についてより丁寧に説明していますので、理解を深めたい方はぜひ一読してみてください。
実際にddofパラメーターに値を指定して、計算をしてみましょう。
print(tmp['Age'].std(ddof=0))
print(tmp['Age'].std(ddof=1))
これら2つのコードの実行結果を以下に示します。
いかがでしょうか。同じ値になったことが分かります。また、standardize関数にもddofパラメーターを持たせることで、scikit-learnのscale関数と同様に標準偏差を求めることもできるでしょう。
def standardize(x, ddof=1):
std = x.std(ddof=ddof)
mean = x.mean()
return (x - mean) / std
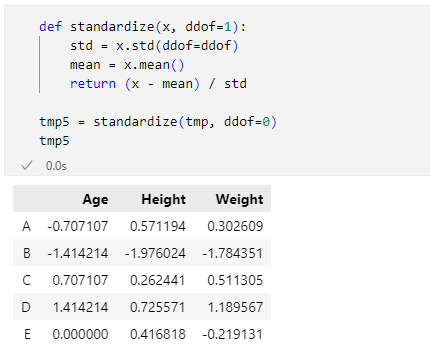
tmp5 = standardize(tmp, ddof=0)
tmp5
実行結果を以下に示します。
DataFrame.stdメソッドのddofパラメーターに0を指定するように、standardize関数を呼び出しているので、scikit-learnのscale関数と同じ結果が得られました。
どうでもよい話をずいぶんとしてきた気もしますが、最後に不偏標準偏差を用いて標準化したDataFrameオブジェクトtmp3が平均0、標準偏差1となっているかどうかを確認しておきます。
ご覧の通り、キチンと標準化できていることが分かりました。
Titanicデータセットを正規化/標準化してみよう
ようやく、Titanicデータセットの登場です。前回に作成したCSVファイルを読み込んでおきます。
df = pd.read_csv('titanic_binned.csv')
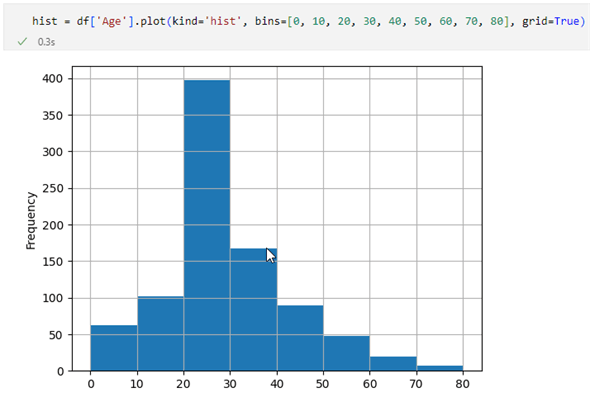
ここまでやることはやってきたので、読み込みが終われば、後は正規化か標準化をするだけです。前回のヒストグラムを見る限り、'Age'列に外れ値はなさそうです。
正規分布に近いと言ってもよいかもしれませんが、少しゆがんでいるような気もします。そこで、ここでは先ほど自分で定義したmin_max_normalize関数を使って'Age'列を正規化することにしました。
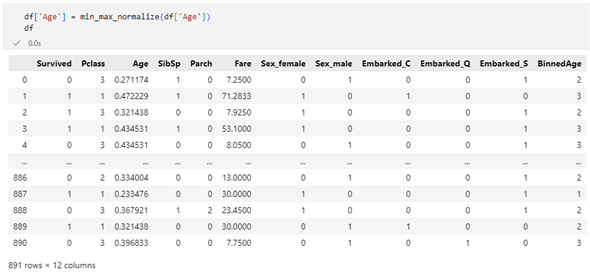
df['Age'] = min_max_normalize(df['Age'])
df
実行結果を以下に示します。
ちゃんと正規化できているようです。機械学習モデルの手法(回帰分析や決定木など)にもよりますが、他の列でも正規化を行い、各列間のスケールをできるだけそろえることで、モデルの訓練過程が安定し、予測精度が向上することがあります。具体的には'Fare'列も正規化できる可能性があるので、それについては次回以降に考えましょう。
Copyright© Digital Advantage Corp. All Rights Reserved.
アイティメディアからのお知らせ
編集部からのお知らせ

 作成したDataFrameオブジェクト
作成したDataFrameオブジェクト
 正規化によってスケーリングされたDataFrameオブジェクト
正規化によってスケーリングされたDataFrameオブジェクト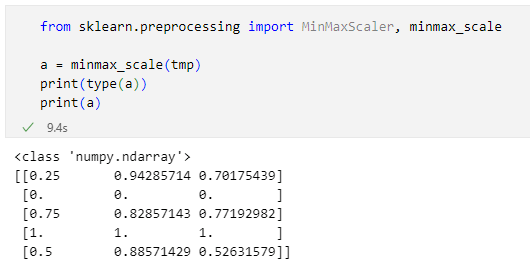 実行結果
実行結果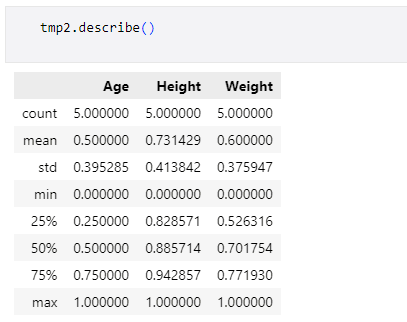 各列について最小値は0に、最大値は1に変換されていることが分かる
各列について最小値は0に、最大値は1に変換されていることが分かる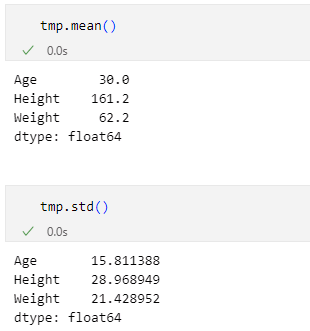 meanメソッドで平均値を、stdメソッドで標準偏差を求める
meanメソッドで平均値を、stdメソッドで標準偏差を求める
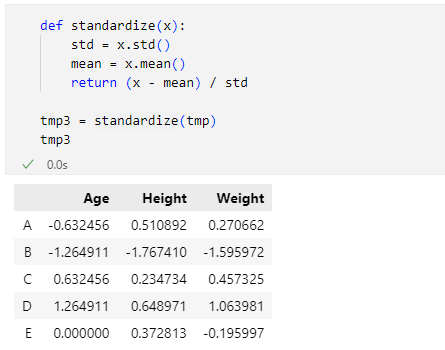 だいたい同じ結果になった
だいたい同じ結果になった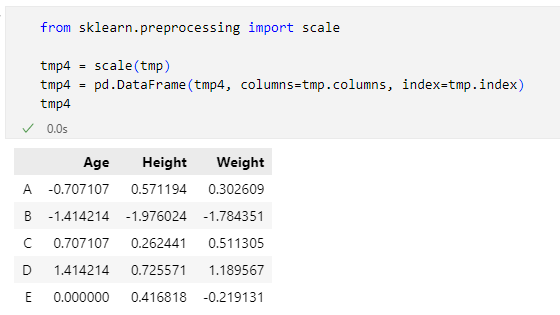 だいたい同じ結果に…‥
だいたい同じ結果に…‥
 実行結果
実行結果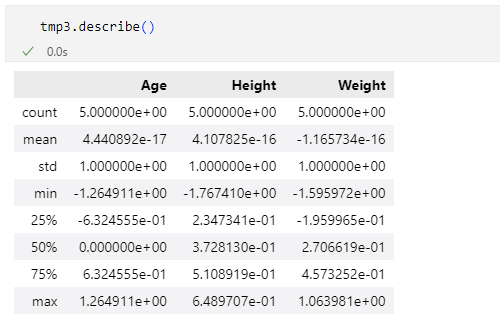 平均はほぼ0で、標準偏差は1になっている
平均はほぼ0で、標準偏差は1になっている