AI・機械学習の数学入門

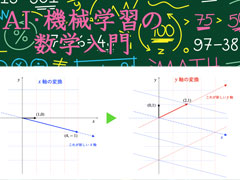
連載の通常の流れとは別の番外編。前回の行列式に続いて、今回は固有値と固有ベクトルについて、ポイントを押さえて見ていく。名付けて「挫折しない固有値・固有ベクトル」というお話（にするつもり）。統計学や機械学習のさまざまな手法の背景にあるこれらの考え方に触れてみよう。

連載の通常の流れとは別の番外編。ベクトルや行列の四則演算から内積あたりまでは比較的スムーズに理解できるのだが、突如、行列式や固有値、固有ベクトルといった謎キャラが登場して挫折してしまう、というのはありがちな話。統計学や機械学習のさまざまな手法の背景にあるこれらの考え方を見ていきたい。

連載の通常の流れとは別の番外編。指数と切っても切れ離せない「対数」を解説。対数関数の性質や対数関数の微分法についても簡単に紹介する。

連載の通常の流れとは別の番外編。AIや機械学習でよく使う「指数」を解説。指数関数の性質や指数関数の微分法についても簡単に紹介する。

統計学や機械学習で使われるさまざまな確率分布のうち、連続分布の例として正規分布とベータ分布について見ていく。また、最近主流になりつつあるベイズ統計の関係についても簡単に紹介する。

分類や推定・予測など、機械学習のさまざまな手法の基礎をなす「確率と統計」における「確率分布」とはどのようなものか。離散分布や連続分布といった種類に分けられるが、その一つである離散分布の例としてベルヌーイ分布と二項分布について見ていく。

確率と統計の基本を踏まえた上で、スパムフィルターをはじめとして幅広く利用されているベイズの定理の考え方や応用について見ていく。

分類や推定、予測など、機械学習のさまざまな手法の基礎をなす確率／統計の基本として、確率の表し方、和事象／積事象／排反事象、独立と従属、条件付き確率をおさらいする。

多くの変数や係数をひとまとめにして取り扱うために、機械学習では行列がよく利用される。前回のベクトルを踏まえて、今回は行列の基本的な計算方法を確認する。さらに、回帰式やニューラルネットワークを行列でどう表現するかを見ていく。

機械学習では、普通、多くの変数や係数を同時に取り扱う。そのような場合にそれぞれの変数や係数を別々に取り扱うと数式が煩雑になってしまう。ベクトルや行列を利用すれば、複数の値をひとまとめにして取り扱えるので、数式が極めて簡潔になる。今回はベクトルについて、基本的な計算方法を紹介する。

微分法は回帰分析だけでなく、機械学習のさまざまなタスクで使われる。特に、合成関数の微分（連鎖律）はニューラルネットワークの学習において必須となる。今回はそのための第一歩として、合成関数がどのようなものであるかを見た後、合成関数の微分法の公式とその計算方法を紹介する。

連載の通常の流れとは別の番外編。「0」の取り扱いについて3つのポイントを解説。0で割ること、0乗、0の階乗について説明する。

これまでに見てきた、説明変数が1つだけの回帰分析と偏微分の基本知識を踏まえて、複数の説明変数がある重回帰分析を行うための基本的な方法を理解しよう。

「偏微分」って何？　いかにも難しそうな名前だが、微分を理解していれば意外に簡単。前回までの知識を踏まえて、今回は偏微分の意味と計算方法を理解しよう。

微分の考え方と計算方法を理解したら、次は微分の公式を押さえて活用してみよう。幾つかの公式を紹介し、応用例として回帰分析を行うための最小二乗法について基本的な考え方を見ていく。

式の値が最小になるときのxの値を求めたり、値がどのように変化していくかを見たりするためには微分が活用できる（回帰分析・重回帰分析につながる基礎知識）。今回は平均変化率から始め、微分の基本を一歩ずつゆっくりと追いかける。

「Σ」を理解して総和をマスターしよう。応用で、Σの公式を使って平均を求めてみる（最小二乗法につながる基礎知識）。さらに、平均を使って重心を求める計算も行う（クラスタリング「k-means法」につながる基礎知識）。

数字（1、2、3、……）の式の次は、文字（a、b、x、y、……）を使った式をおさらいしよう。これまでに学んだ知識と平方完成を使って、距離の二乗和の最小値を求める計算も行う。

機械学習の数学は難しい!? そう思っている人はここから学んでみよう。本連載では、小学校で習う「四則演算（足し算／引き算／掛け算／割り算）」を使って、機械学習の数学をできるだけ分かりやすく簡単に説明していく。だからサブタイトルは「― 中学／高校数学のキホンから学べる」。今回は距離を求める中学数学をおさらいする。